Развертка трапеции: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника ✅ igrad.su

развертка. Развертка пирамиды для склеивания. Развертки из бумаги

Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.

Материалы и приспособления

Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:

• бумага или картон;
• ножницы;
• карандаш;
• линейка;
• циркуль;
• ластик;
• клей.

Определение параметров

Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.

Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.

Как выполняется развертка правильной пирамиды?

Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.

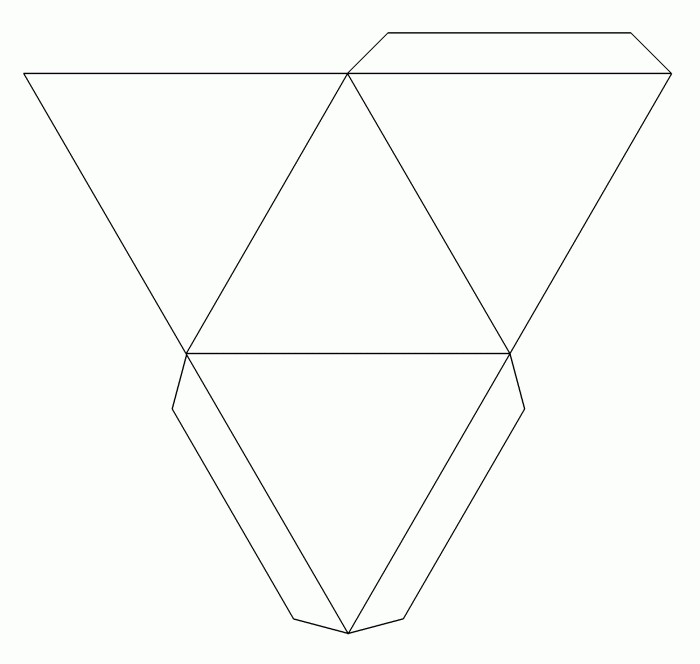Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды – треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.

Сборка макета

Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.

Развертка четырехугольной пирамиды

Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.

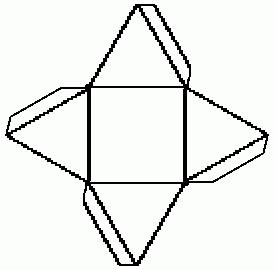
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.

Завершающий этап выполнения макета

Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.

Объемные макеты сложных фигур

После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.

Построение чертежа

Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.

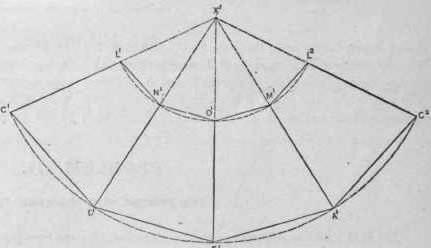
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.

Завершение моделирования

Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.

Изготовление разных моделей многогранников

Выполнение объемных моделей геометрических фигур — увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.

Тела вращения — Развертки — Mnogogranniki.ru

Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон? 

Одним лишь вращением мы можем создать новое геометрическое тело в пространстве.

Боковые поверхности цилиндра образуются за счет сторон вращающегося прямоугольника.

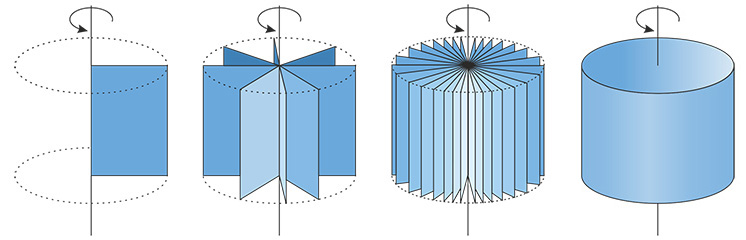
Официальное определение для таких геометрических тел, звучит следующим образом:
Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.

И здесь важно то, что плоская геометрическая фигура может быть совершенно произвольной формы.

Например, кривая, которая при вращении будет образовывать вазу или лампочку. Такие инструменты создания тел вращения очень популярны у тех, кто работает в программах 3D-проектирования.

Но с математической точки зрения, для нас, прежде всего, интересны следующие геометрические тела вращения:

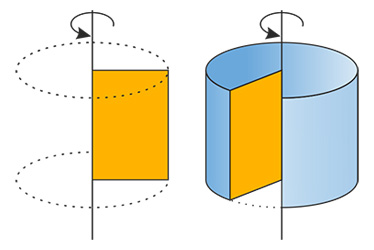
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон.

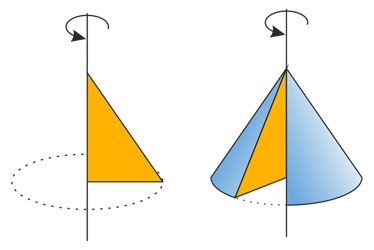
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов.

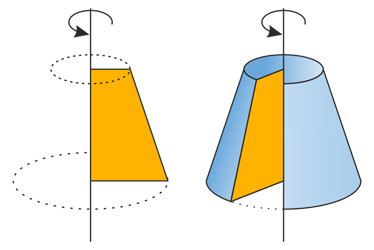
Усечённый конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.

Образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции.

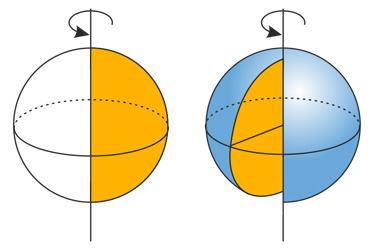
Шар — образован полукругом, вращающимся вокруг диаметра разреза.

При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).

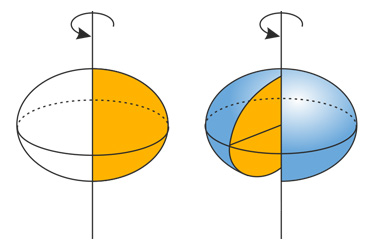
Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.

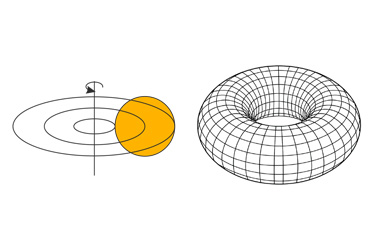
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его.

В обычном понимании тор — это «бублик».

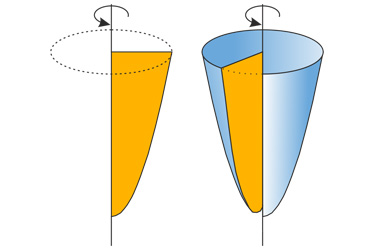
Параболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком параболы. Отсюда и название параб-о-лоид.  

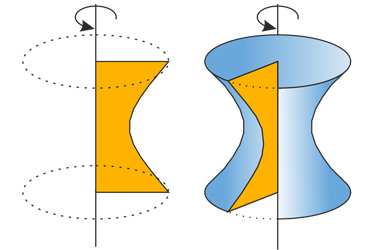
Гиперболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком гиперболы. Соответственно название гиперб-о-лоид.

Как сделать цилиндр из бумаги?

Как сделать конус из бумаги?

Как сделать параболоид из бумаги?

Как сделать гиперболоид из бумаги?

Как сделать тор из бумаги?

Для сопоставимости размеров получающихся моделей тел вращения мы постарались собрать их на одной поверхности вместе с призмами из выпуска «Волшебные грани № 16».

Получился целый математический город из бумаги, умещающийся на столе!

ПОСТРОЕНИЕ РАЗВЕРТОК ПОВЕРХНОСТЕЙ Методические рекомендации по курсу начертательной геометрии

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Алтайский государственный технический университет им. И.И. Ползунова»

Бийский технологический институт (филиал)

Г.И. Куничан, Л.И. Идт

ПОСТРОЕНИЕ РАЗВЕРТОК

ПОВЕРХНОСТЕЙ

Методические рекомендации по курсу начертательной геометрии

для самостоятельной работы студентов механических специальностей

171200, 120100, 171500, 170600

Бийск

2005

УДК 515.0(075.8)

Куничан Г.И., Идт Л.И . Построение разверток поверхностей:

Методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600.

Алт. гос. техн. ун-т, БТИ. – Бийск.

Изд-во Алт. гос. техн. ун-та, 2005. – 22с.

В методических рекомендациях подробно рассмотрены примеры построения разверток многогранников и поверхностей вращения по теме построение разверток поверхностей курса начертательной геометрии, которые изложены в виде лекционного материала. Методические рекомендации предлагаются для самостоятельной работы студентов дневной, вечерней и заочной форм обучения.

Рассмотрены и одобрены

на заседании

кафедры

технической

графики.

Протокол №20 от 05.02.2004 г.

Рецензент: завкафедрой МРСиИ БТИ АлтГТУ, к.т.н. Фирсов А.М.

 Куничан Г.И., Идт Л.И., Леонова Г.Д., 2005

БТИ АлтГТУ, 2005

ОБЩИЕ ПОНЯТИЯ О РАЗВЕРТЫВАНИИ ПОВЕРХНОСТЕЙ

Представляя поверхность в виде гибкой, но нерастяжимой пленки, можно говорить о таком преобразовании поверхности, при котором поверхность совмещается
с плоскостью без складок и разрывов. Следует указать, что далеко не каждая поверхность допускает такое преобразование. Ниже будет показано, какие типы поверхностей возможно совместить с плоскостью при помощи изгибания, без растяжения и сжатия.

Поверхности, которые допускают такое преобразование, называются развертывающимися, а фигура на плоскости, в которую поверхность преобразуется, называется разверткой поверхности.

Построение разверток поверхностей имеет большое практическое значение при конструировании различных изделий из листового материала. При этом необходимо отметить, что часто приходится изготовлять из листового материала не только развертывающиеся поверхности, но и неразвертывающиеся поверхности. В этом случае неразвертывающуюся поверхность разбивают на части, которые можно приближенно заменить развертывающимися поверхностями, а затем строят развертки этих частей.

К числу развертывающихся линейчатых поверхностей относятся цилиндрические, конические и торы.

Все остальные кривые поверхности не развертываются на плоскость и поэтому при необходимости изготовления этих поверхностей из листового материала их приближенно заменяют развертывающимися поверхностями.

1 ПОСТРОЕНИЕ РАЗВЕРТОК ПИРАМИДАЛЬНЫХ

ПОВЕРХНОСТЕЙ

Построение разверток пирамидальных поверхностей приводит к многократному построению натурального вида треугольников, из которых состоит данная пирамидальная поверхность или многогранная поверхность, вписанная (или описанная) в какую-либо коническую или линейчатую поверхность, которой заменяется указанная поверхность. Описываемый способ приводит к разбивке поверхности на треугольники, он называется способом треугольников (триангуляции).

Покажем применение этого способа для пирамидальных поверхностей. Если пренебречь графическими ошибками, то построенные развертки таких поверхностей можно считать точными.

Пример 1. Построить полную развертку поверхности части треугольной пирамиды SABC.

Так как боковые грани пирамиды являются треугольниками, то для построения ее развертки нужно построить натуральные виды этих треугольников. Для этого предварительно должны быть определены натуральные величины боковых ребер. Натуральную величину боковых ребер можно определить при помощи прямоугольных треугольников, в каждом из которых одним катетом является превышение точки S над точками А, В и С, а вторым катетом – отрезок, равный горизонтальной проекции соответствующего бокового ребра (рисунок 1).

Так как стороны нижнего основания являются горизонталями, то их натуральные величины можно измерить на плоскости П₁. После этого каждая боковая грань строится как треугольник по трем сторонам. Развертка боковой поверхности пирамиды получается в виде ряда примыкающих один к другому треугольников с общей вершиной S (S₂C*, S₂A*, S₂B* – являются натуральными величинами ребер пира-миды).

Для нанесения на развертку точек D, E и F, соответствующих вершинам сечения пирамиды плоскостью, нужно предварительно определить их натуральные расстояния от вершины S, для чего следует перенести точки D*, E* и F* на соответствующие натуральные величины боковых ребер.

Рисунок 1

После построения развертки боковой поверхности усеченной части пирамиды, следует пристроить к ней треугольники АВС и DEF. Треугольник АВС является основанием усеченной пирамиды и изображен на горизонтальной плоскости проекций в натуральную величину.

2 ПОСТРОЕНИЕ РАЗВЕРТОК КОНИЧЕСКИХ

ПОВЕРХНОСТЕЙ

Рассмотрим построение разверток конических поверхностей. Несмотря на то, что конические поверхности являются развертывающимися и, следовательно, имеют теоретически точные развертки, практически строят их приближенные развертки, пользуясь способом треугольников. Для этого заменяют коническую поверхность вписанной в нее поверхностью пирамиды.

Пример 2. Построить развертку прямого конуса с отсеченной вершиной (рису-нок 2а, б).

1. Необходимо предварительно построить развертку боковой поверхности конуса. Этой разверткой является круговой сектор, радиус которого равен натуральной величине образующей конуса, а длина дуги равна длине окружности основания конуса. Практически дугу сектора определяют при помощи ее хорд, которые принимают равными хордам, стягивающим дуги основания конуса. Иначе говоря, поверхность конуса заменяется поверхностью вписанной пирамиды.

2. Чтобы на развертку нанести точки фигуры сечения (А,В,С,D,F,G,K), нужно предварительно определить их натуральные расстояния от вершины S, для чего следует перенести точки А₂, В₂, С₂, D₂, F₂, G₂, K₂ на соответствующие натуральные величины образующих конуса. Так как в прямом конусе все образующие равны, то достаточно перенести проекции точек сечения на крайние образующие S₂1₂ и S₂7₂. Таким образом, отрезки S₂A*, S₂B*, S₂D*, S₂F*, S₂G*, S₂K* являются искомыми, т.е. равными натуральной величине расстояния от S до точек сечения.

Рисунок 2 (а)

Рисунок 2 (б)

Пример 3. Построить развертку боковой поверхности эллиптического конуса с круговым основанием (рисунок 3).

В данном примере коническая поверхность заменяется поверхностью вписанной двенадцатиугольной пирамиды. Так как коническая поверхность имеет плоскость симметрии, то можно построить развертку только одной половины поверхности. Разделив от точки О половину окружности основания конической поверхности на шесть равных частей и определив с помощью прямоугольных треугольников натуральные величины образующих, проведенных в точки деления, строим шесть примыкающих один к другому треугольников с общей вершиной S.

Каждый из этих треугольников строится по трем сторонам; при этом две стороны равны натуральным величинам образующих, а третья – хорде, стягивающей дугу окружности основания между соседними точками деления (например О₁-1₁, 1₁-2₁, 2₁— 3₁ и т.д.) После этого через точки 0, 1, 2 … разогнутого по способу хорд основания конической поверхности проводится плавная кривая.

Если на развертке надо нанести какую-либо точку М, находящуюся на поверхности конуса, то следует предварительно построить точку М* на гипотенузе S₂ –7* прямоугольного треугольника, с помощью которого определена натуральная величина образующей S – 7, проходящей через точку М. После этого следует провести на развертке прямую S – 7, определив точку 7 из условия равенства хорд 2₁ – 7₁=2 – 7, и на ней отложить расстояние SM=S₂M*.

Рисунок 3

3 ПОСТРОЕНИЕ РАЗВЕРТОК ПРИЗМАТИЧЕСКИХ

И ЦИЛИНДРИЧЕСКИХ ПОВЕРХНОСТЕЙ

Построение разверток призматических и цилиндрических поверхностей приводит в общем случае к многократному построению натурального вида трапеций, из которых состоит данная призматическая поверхность, или призматическая поверхность, вписанная (или описанная) в цилиндрическую поверхность и заменяющая ее. Если, в частности, призматическая или цилиндрическая поверхности ограничены параллельными основаниями, то трапеции, на которые разбивается поверхность, обращаются в прямоугольники или параллелограммы, в зависимости от того, перпендикулярны или нет плоскости оснований боковым ребрам или образующим поверхности.

Построение трапеций или параллелограммов проще всего произвести по их основаниям и высотам, причем необходимо также знать отрезки оснований, на которые они делятся высотой. Поэтому для построения развертки призматической или цилиндрической поверхности необходимо предварительно определить натуральный вид нормального сечения данной поверхности. Стороны этого сечения, в случае призматической поверхности, и будут высотами трапеций или параллелограммов, из которых состоит поверхность. В случае цилиндрической поверхности высотами будут хорды, стягивающие дуги нормального сечения, на которые разделена кривая, ограничивающая это сечение.

Так как указанный способ требует построения нормального сечения, то он называется способом нормального сечения.

Покажем применение этого способа для призматических поверхностей. Если пренебречь графическими ошибками, то построенные развертки этих поверхностей можно считать точными.

Пример 4. Построить полную развертку поверхности треугольной призмы АВСDEF (рисунок 4).

Пусть данная призма расположена относительно плоскостей проекций так, что ее боковые ребра являются фронталями. Тогда они проецируются на плоскость проекций П₂ в натуральную величину и фронтально проецирующая плоскость S_v, перпендикулярная боковым ребрам, определит нормальное сечение PQR призмы.

Построив натуральный вид P₄Q₄R₄ этого сечения, найдем натуральные величины P₄Q₄ , Q₄R₄ и R₄P₄ — высот параллелограммов, из которых состоит боковая поверхность призмы.

Рисунок 4

Так как боковые ребра призмы параллельны между собой, а стороны нормального сечения им перпендикулярны, то из свойства сохранения углов на развертке следует, что на развертке призмы боковые ребра будут также параллельны между собой, а стороны нормального сечения развернутся в одну прямую. Поэтому для построения развертки призмы нужно отложить на произвольной прямой натуральные величины сторон нормального сечения, а затем через их концы провести прямые,

перпендикулярные к этой прямой. Если теперь отложить на этих перпендикулярах

по обе стороны от прямой QQ отрезки боковых ребер, измеренные на плоскости проекций П₂, и соединить отрезками прямых концы отложенных отрезков, то получим развертку боковой поверхности призмы. Присоединяя к этой развертке оба основания призмы, получим ее полную развертку.

Если боковые ребра данной призмы имели бы произвольное расположение относительно плоскостей проекций, то нужно было бы предварительно преобразовать их в прямые уровня.

Существуют также другие способы построения разверток призматических поверхностей, один из которых – раскатка на плоскости – рассмотрим на примере 5.

Пример 5. Построить полную развертку поверхности треугольной призмы ABCDEF (рисунок 5).

Рисунок 5

Эта призма расположена относительно плоскостей проекций так, что ее ребра являются фронталями, т.е. на фронтальной плоскости проекций П₂ изображены в натуральную величину. Это позволяет использовать один из методов вращения, позволяющих находить натуральную величину фигуры путем вращения ее вокруг прямой уровня. В соответствии с этим методом точки B,C,A,D,E,F, вращаясь вокруг ребер AD, BE и CF, совмещаются с фронтальной плоскостью проекций. Т.е. траектория движения точек В_{2и F2 изобразится перпендикулярно A2 D2.}

Раствором циркуля, равным натуральной величине отрезка АВ (АВ=А₁В₁),из точек А₂ и D₂ делаем засечки на траектории движения точек В_{2и F2. Полученная грань A2D2BF изображена в натуральную величину. Следующие две грани BFCEи CEAD строим аналогичным способом. Пристраиваем к развертке два основания АВС и DEF. Если призма расположена так, что ее ребра не являются прямыми уровня, то используя методы преобразования чертежа (замены плоскостей проекций или вращения), следует провести преобразование так, чтобы ребра призмы стали прямыми уровня.}

Рассмотрим построение разверток цилиндрических поверхностей. Хотя цилиндрические поверхности являются развертывающимися, практически строят приближенные развертки, заменяя их вписанными призматическими поверхностями.

Пример6. Построить развертку прямого цилиндра, усеченного плоскостью Sv (рисунок 6).

Рисунок 6

Построение развертки прямого цилиндра не представляет никакой сложности, т.к. является прямоугольником, длина одной стороны равняется 2πR, а длина другой равна образующей цилиндра. Но если требуется нанести на развертку контур усеченной части, то построение целесообразно вести, вписав в цилиндр двенад-цатигранную призму. Обозначим точки сечения (сечение является эллипсом), лежащие на соответствующих образующих, точками 1₂, 2₂, 3₂ … и по линиям связи
перенесем их на развертку цилиндра. Соединим эти точки плавной линией и пристроим натуральную величину сечения и основание к развертке.

Если цилиндрическая поверхность наклонная, то развертку можно строить двумя способами, рассмотренными ранее на рисунках 4 и 5.

Пример 7. Построить полную развертку наклонного цилиндра второго порядка (рисунок 7).

Рисунок 7

Образующие цилиндра параллельны плоскости проекций П_2, т.е. изображены на фронтальной плоскости проекций в натуральную величину. Основание цилиндра делят на 12 равных частей и через полученные точки проводят образующие. Развертку боковой поверхности цилиндра строят так же, как была построена развертка наклонной призмы, т.е. приближенным способом.

Для этого из точек 1₂, 2₂, …, 12₂ опускают перпендикуляры к очерковой образующей 1А и радиусом, равным хорде 1₁2₁, т.е. 1/12 части деления окружности основания, последовательно делают засечки на этих перпендикулярах. Например, делая засечку из точки 1₂ на перпендикуляре, проведенном из точки 2₂, получают 2. Принимая далее точку 2 за центр, тем же раствором циркуля делают засечку на перпендикуляре, проведенном из точки 3₂, и получают точку 3 и т.д. Полученные точки 1₂, 2, 3,…, 1 соединяют плавной лекальной кривой. Развертка верхнего основания симметрична развертке нижнего, так как сохраняется равенство длин всех образующих цилиндра.

4 ПРИБЛИЖЕННОЕ РАЗВЕРТЫВАНИЕ ШАРОВОЙ ПОВЕРХНОСТИ

Шаровая поверхность относится к так называемым неразвертываемым поверхностям, т. е. к таким, которые не могут быть совмещены с плоскостью, не претерпев при этом каких-либо повреждений (разрывов, складок). Таким образом, шаровая поверхность может быть развернута лишь приближенно.

Один из способов приближенной развертки шаровой поверхности рассмотрен на рисунке 8.

Сущность этого приема состоит в том, что шаровая поверхность при помощи меридианальных плоскостей, проходящих через ось шара SP, разбивается на ряд одинаковых частей.

На рисунке 8 шаровая поверхность разбита на 12 равных частей и показана горизонтальная проекция (s₁, k₁, l₁)только одной такой части. Затем дуга k4lзаменена прямой (m₁n₁), касательной к окружности, и эта часть шаровой поверхности заменена цилиндрической поверхностью с осью, проходящей через центр шара и параллельной касательной тп. Далее дуга s₂4₂разделена на четыре равные части. Точки 1₂, 2₂, 3₂, 4₂приняты за фронтальные проекции отрезков образующих цилиндрической поверхности с осью, параллельной тп. Их горизонтальные проекции: a₁b₁, c₁d₁, e₁f₁, т₁п₁. Затем на произвольной прямой MNотложен отрезок тп. Через его середину проведен перпендикуляр к MNи на нем отложены отрезки 4₂3₂, 3₂2₂, 2₂1₂, 1₂S₂, равные соответствующим дугам 4₂3₂, 3₂2₂, 2₂1₂, 1₂s₂. Через полученные точки проведены линии, параллельные тп, и на них отложены соответственно отрезки а₁b₁, c₁d₁, e₁f₁. Крайние точки этих отрезков соединены плавной кривой. Получилась развертка ¹/₁₂ части шаровой поверхности. Очевидно, для построения полной развертки шара надо вычертить 12 таких разверток.

5 ПОСТРОЕНИЕ РАЗВЕРТКИ КОЛЬЦА

Пример 9. Построить развертку поверхности кольца (рисунок 9).

Разобьем поверхность кольца при помощи меридианов на двенадцать равных частей и построим приближенную развертку одной части. Заменяем поверхность этой части описанной цилиндрической поверхностью, нормальным сечением которой будет средний меридиан рассматриваемой части кольца. Если теперь спрямить этот меридиан в отрезок прямой и через точки деления провести перпендикулярно к нему образующие цилиндрической поверхности, то, соединив их концы плавными кривыми, получим приближенную развертку 1/12 части поверхности кольца.

Рисунок 8

Рисунок 9

6 ПОСТРОЕНИЕ РАЗВЕРТКИ ВОЗДУХОВОДА

В заключение покажем построение развертки поверхности одной технической детали, изготовляемой из листового материала.

На рисунке 10 изображена поверхность, с помощью которой осуществляется переход с квадратного сечения на круглое. Эта поверхность состоит из двух
конических поверхностей I, двух конических поверхностей II, двух плоских треугольников IIIи плоских треугольников IVи V.

Рисунок 10

Для построения развертки данной поверхности нужно предварительно определить натуральные величины тех образующих конических поверхностей I и II, спомощью которых эти поверхности заменяются совокупностью треугольников. На вспомогательном чертеже по способу прямоугольного треугольника построены натуральные величины этих образующих. После этого строят развертки конических поверхностей, а между ними в определенной последовательности строят треугольники III, IVи V, натуральный вид которых определяется по натуральной величине их сторон.

На чертеже (см. рисунок 10) показано построение развертки части от данной поверхности. Для построения полной развертки воздуховода следует достроить конические поверхности I, II и треугольник III.

Рисунок 11

На рисунке 11 приведен пример развертки воздуховода, поверхность которого можно разбить на 4 одинаковые цилиндрические поверхности и 4 одинаковые треугольника. Цилиндрические поверхности представляют собой наклонные цилиндры. Метод построения развертки наклонного цилиндра методом раскатки приведен подробно ранее на рисунке 7. Более удобным и наглядным для данной фигуры методом построения развертки представляется метод триангуляции, т.е. цилиндрическая поверхность разбивается на треугольники. А затем определяется натуральная величина сторон методом прямоугольного треугольника. Построение развертки цилиндрической части воздуховода обоими способами приведено на рисунке 11.

Вопросы для самоконтроля

1. Укажите приемы построения разверток цилиндрических и конических поверхностей.

2. Как построить развертку боковой поверхности усеченного конуса, если нельзя достроить этот конус до полного?

3. Как построить условную развертку сферической поверхности?

4. Что называется разверткой поверхности?

5. Какие поверхности относятся к развертывающимся?

6. Перечислите свойства поверхности, которые сохраняются на ее развертке.

7. Назовите способы построения разверток и сформулируйте содержание каждого из них.

8. В каких случаях для построения развертки используются способы нормального сечения, раскатки, треугольников?

Литература

Основная литература

1. Гордон, В.О.  Курс начертательной геометрии / В.О. Гордон, М.А. Семенцо-Огиевский; под ред. В.О. Гордона. – 25-е изд., стер. – М.: Высш. шк., 2003.

2. Гордон, В.О.  Сборник задач по курсу начертательной геометрии / В.О. Гордон, Ю.Б. Иванов, Т.Е. Солнцева; под ред. В.О. Гордона. – 9-е изд., стер. – М.:  Высш. шк., 2003.

3. Курс начертательной геометрии / под ред. В.О. Гордона. – 24-е изд, стер. – М.: Выcшая школа, 2002.

4. Начертательная геометрия / под ред. Н.Н. Крылова. – 7-е изд., перераб. и доп.- М.: Выcшая школа, 2000.

5. Начертательная геометрия. Инженерная и машинная графика: программа, контрольные задания и методические указания для студентов-заочников инже-нерно-технических и педагогических специальностей вузов / А.А. Чекмарев, 
А.В. Верховский, А.А. Пузиков; под ред. А.А. Чекмарева. – 2-е изд., испр. – М.: Выcшая школа, 2001.

Дополнительная литература

6. Фролов, С.А. Начертательная геометрия / С.А. Фролов. – М.: Машиностроение, 1978.

7. Бубенников, А.В. Начертательная геометрия / А.В. Бубенников, М.Я. Громов. – М.: Высшая школа, 1973.

8. Начертательная геометрия / под общей ред. Ю.Б. Иванова. – Минск: Вышейшая школа, 1967.

9. Боголюбов, С.К. Черчение: учебник для машиностроительных специальностей средних специальных учебных заведений / С.К. Боголюбов. – 3-е изд., испр. и дополн. – М.: Машиностроение, 2000.

СОДЕРЖАНИЕ

Общие понятия о развертывании поверхностей…………………………………………3

1 Построение разверток пирамидальных поверхностей………………………………..3

2 Построение разверток конических поверхностей………………………………….….5

3 Построение разверток призматических и цилиндрических поверхностей………….9

4 Приближенное развертывание шаровой поверхности………………………….….. 14

5 Построение развертки кольца………………………………………………………….14

6 Построение развертки воздуховода……………………………………………………16

Вопросы для самоконтроля………………………………………………………………19

Литература………………………………………………………………………………..20

Куничан Галина Ивановна

Идт Любовь Ивановна

Построение разверток поверхностей

Методические рекомендации по курсу начертательной геометрии для самостоятельной работы студентов механических специальностей 171200, 120100, 171500, 170600

Редактор Идт Л.И.

Технический редактор Малыгина Ю.Н.

Корректор Малыгина И.В.

Подписано в печать 25.01.05. Формат 61х86 /8.

Усл. п. л. 2,67. Уч.-изд. л. 2,75.

Печать – ризография, множительно-копировальный

аппарат «RISO TR -1510»

Тираж 60 экз. Заказ 2005-06.

Издательство Алтайского государственного

технического университета,

656099, г. Барнаул, пр.-т Ленина, 46

Оригинал-макет подготовлен ИИЦ БТИ АлтГТУ.

Отпечатано в ИИЦ БТИ АлтГТУ.

659305, г. Бийск, ул. Трофимова, 29

Г.И. Куничан, Л.И. Идт

ПОСТРОЕНИЕ РАЗВЕРТОК ПОВЕРХНОСТЕЙ

Методические рекомендации по курсу начертательной геометрии

для самостоятельной работы студентов механических специальностей

171200, 120100, 171500, 170600

Бийск

2005

Онлайн калькулятор: Развертка (выкройка) сферы

Калькулятор рассчитывает параметры развертки сферы на плоскости. Картинка ниже иллюстрирует задачу.

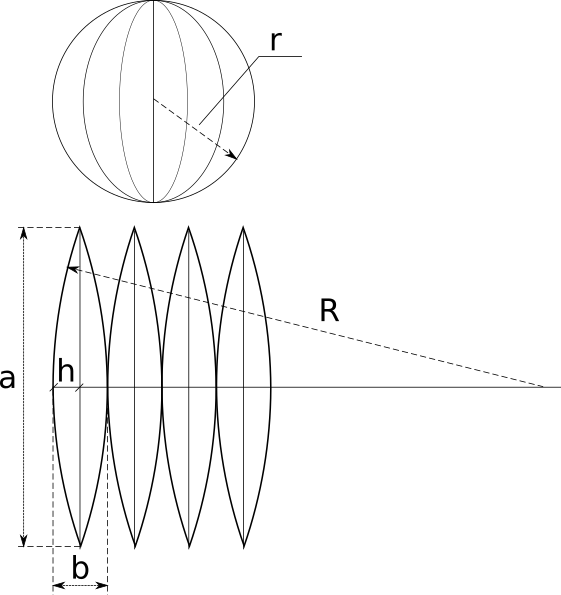
Итак, нам известен радиус сферы r и число долей на которое мы хотим ее разбить n. Для описания развертки нам надо найти высоту «дольки» a, ширину «дольки» b, и радиус R большой дуги, на которой построена «долька». Формулы расчета и объяснения, как обычно, приведены под калькулятором.

Развертка сферы

Сгенерировать точки разверткиТочность вычисления

Знаков после запятой: 2

Высота доли (а)

 

Ширина доли (b)

 

Высота сегмента (h)

 

Радиус дуги (R)

 

save Сохранить extension Виджет

С высотой все понятно — это половина длины окружности, которую можно получить при сечении сферы плоскостью, проходящей через центр. Таким образом,
.
С шириной тоже все понятно — это часть той же окружности, полученная при разбиении всей окружности на n частей:

Радиус дуги можно вычислить по длине хорды (это а) и высоте сегмента (это h=b/2) по следующей формуле (см. Сегмент круга).

В принципе, найдя a и b, считать радиус R даже не обязательно — его можно найти по построению, что иллюстрирует следующая картинка.

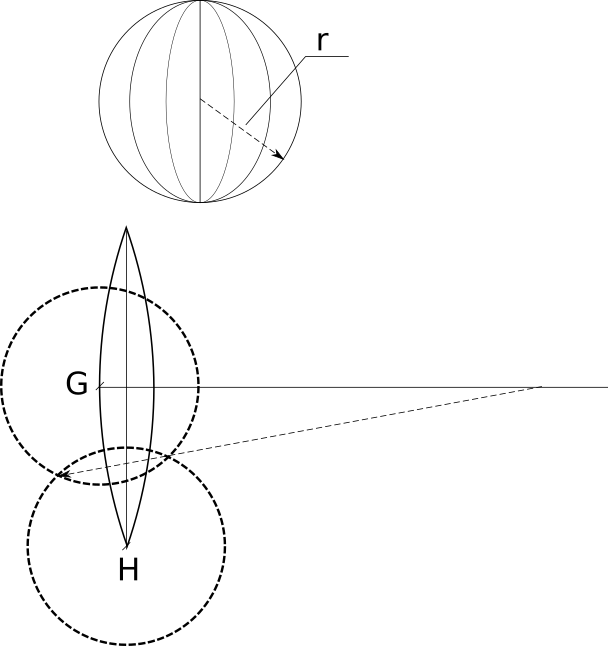
Для нахождения радиуса из точек G и H надо провести две окружности, так, чтобы они пересекались — прямая, проведенная через точки пересечения, пересечет среднюю линию в точке центра окружности, на дуге которой лежат G и H.

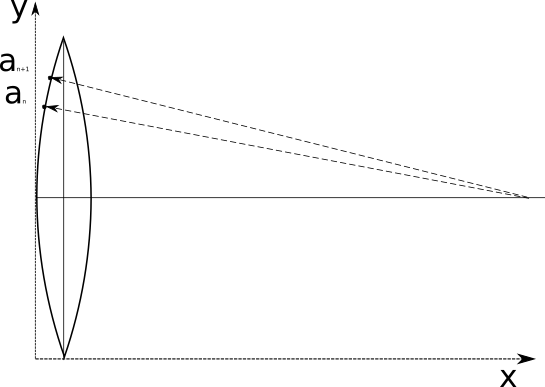
Несмотря на всю простоту, у метода есть один недостаток — а именно, ему нужно очень много места сбоку для радиуса, и чем больше число долек, на которое мы хотим разбить сферу, тем больше радиус большой дуги. Не везде будет возможность найти столько места и такой большой «циркуль», чтобы нарисовать дугу. Поэтому калькулятор, кроме расчета параметров «дольки», также рассчитывает координаты точек, лежащих на дуге — можно строить дуги дольки по точкам, не используя радиус. Для того, чтобы рассчитать координаты точек, надо пометить флажок «Сгенерировать точки развертки», и указать число точек — дуга будет разбита на заданное число точек с равным угловым шагом, как показано на рисунке:

Пять способов рисования трапеций. | CorelTUTORIALS

В этом уроке вы узнаете пять различных способов, как быстро нарисовать трапецию, используя такие инструменты, как «Основные фигуры», «Форма», «Прямоугольник» а также освоите различные команды для преобразований в CorelDRAW.

Оказывается иногда и простая фигура может поставить начинающего пользователя в тупик. И вправду, как вот так, сразу, нарисовать трапецию.

Рис. 1. Примеры трапеций.

Способ первый. «Простейший».

Активируем инструмент «Основные фигуры». Выбираем подгруппу «Правильные фигуры». В мини–библиотеке, которая появилась на панели свойств, выбираем нужную фигуру и рисуем ее на рабочем листе документа.

Рис. 2. После активирования инструмента «Основные фигуры», на панели свойств появится список правильных фигур.

Рис. 3. Перемещение глифа (красного маркера) позволяет редактировать форму объекта.

В левом верхнем углу нарисованной трапеции появляется красный маркер в форме ромба. Этот маркер называется глифом. Вид трапеции или любой другой фигуры из группы основных фигур изменяется, путем перетаскивания глифа инструментом «Форма». При наведении инструмента на глиф, курсор изменится и глиф можно будет переместить.

Способ второй. «Перспективный».

Активируем инструмент «Прямоугольник» и рисуем произвольный прямоугольник. Выделяем его и в меню «Эффекты» выбираем пункт «Добавить перспективу».
Инструментом «Форма» перемещаем верхние маркеры на одной из сторон прямоугольника. Можно перемещать и точку схождения перспективы, добиваясь нужного наклона сторон трапеции.

Рис. 4. С помощью меню «Эффекты» можно добавить объекту перспективу.

Рис.5. Перемещая маркеры перспективы, или изменяя положение точки схода легко добиться нужного эффекта.

После применения эффекта перспективы, в статусной строке программы появится информация о том, что к объекту был применен эффект перспективы. Можно сразу же преобразовать объект с примененным эффектом в простую кривую командой меню «Объект» > «Преобразовать в кривую». Форма объекта будет сохранена.

Способ третий. «Конструктор».

Инструментом «Прямоугольник» рисуем основной объект — квадрат или прямоугольник.
Удерживаем во время рисования инструментом «Прямоугольник клавишу Сtrl – рисуем квадрат.
Удерживаем во время рисования клавишу «Shift» – рисуем прямоугольник не от угла, а от центра.
Удерживаем во время рисования обе клавиши Сtrl+Shift – рисуем квадрат от центра.

Выставляем по сторонам прямоугольника (квадрата) направляющие. Включаем «привязку к направляющим». Это можно сделать соответствующей командой меню «Вид» > «Привязать к» > «Направляющим».

Рис.6. В меню «Вид» можно включить нужный режим привязки объекта.

Рис.7. Привязка прямоугольников к направляющим.

Рисуем еще два одинаковых прямоугольника, с высотой, соответствующей высоте базового основного прямоугольника. Размещаем эти объекты слева и справа от основного, базового прямоугольника вплотную к нему. Поскольку включен режим привязки к направляющим, то не составит большого труда правильно расположить объекты.
Преобразуем левый и правый прямоугольники в кривые, командой «Объект» > «Преобразовать в кривую» или используя комбинацию клавиш «Ctrl+ Q».
Инструментом «Форма» удаляем по одному углу во вспомогательных прямоугольниках.

Рис.8. Удаление одного из узлов прямоугольника.

Выделяем инструментом выбора все три фигуры и применяем команду меню «Объект» > «Формирование» > « Объединение» или нажимаем на кнопку этой же команды на панели свойств.

Рис.9. Вызов команды объединения объектов.

Рис.10. Так выглядит фигура после объединения.

Способ четвертый. «Рисование по сетке или направляющим».

Сначала включаем режим отображения сетки документа. Это можно сделать командой меню «Вид»> «Сетка»> «Сетка документа» либо включить на съемной панели быстрого вызова команд меню.

Рис.11. Включение отображения сетки документа.

На этой же панели находится и кнопка включения различных режимов привязки, включаем режим привязки «сетка документа»

Рис.12. Включение режима привязки объектов.

Теперь можно активировать инструмент «Прямая через две точки» и рисовать трапецию нужного размера. Узлы фигуры будут надежно привязаны к узлам сетки документа. Не забудьте проверить включен ли режим автоматического замыкания полученной кривой.

Рис.13. Работа с инструментом «Прямая через две точки».

Кстати если режим привязки к сетке включен, а сама сетка документа невидима, то во время рисования фигуры сохранится способность притяжения к сетке и фигура будет нарисована именно по сетке.

Точно таким же образом можно нарисовать трапецию или любую другую сложную фигуру, используя привязку к направляющим. Сначала выставляются направляющие по размеру будущей фигуры, затем включается режим привязки к направляющим и рисуется собственно фигура.

Рис.14. Рисование трапеции по направляющим.

Способ пятый. «Симметричные узелки».

Наверное, самый простой способ рисования трапеции – преобразовать в нее обычный прямоугольник. Сначала придется просто преобразовать прямоугольник в кривую (комбинация клавиш «Ctrl+Q») и, затем, поочередно инструментом «Форма» переместить два параллельных узла на нужное расстояние. Для точности удобно воспользоваться направляющими и включить соответствующий режим привязки.

Рис.15. Рисование трапеции из прямоугольника.

Таким способом легко рисовать самые разнообразные трапеции – остроугольные, тупоугольные, прямоугольные.

Рис.16. Примеры трапеций.

А вот если необходимо нарисовать равнобедренную трапецию, лучше применить способ симметричного перемещения узлов.
Рисуем прямоугольник, преобразуем его в кривую. Активируем инструмент «Форма», выделяем этим инструментом два параллельных узла. На панели свойств включаем режим «Отразить узлы по горизонтали» и начинаем передвигать выделенные ранее узлы. Оба узла будут перемещаться симметрично до нужного положения.

Рис.17. Симметричное перемещение узлов по горизонтали.

Аналогичным образом можно перемещать узлы, включая режим «отразить по вертикали».

Рис.18. Симметричное перемещение узлов по вертикали.

Работа в режиме отражения узлов по вертикали или горизонтали значительно упрощает работу при рисовании симметричных фигур.

На панели свойств инструмента «Форма» есть еще несколько очень интересных кнопок, позволяющих масштабировать и поворачивать отдельные узлы кривых.

Рис.19. Включение режима «Повернуть или наклонить узел» позволит переместить, наклонить, повернуть один или несколько узлов и создать новую фигуру.

Навыки рисования трапеций различными способами всегда пригодятся при рисовании других простых или сложных фигур.

Презентация по теме «Тела вращения»

Описание презентации по отдельным слайдам:

1 слайд

Описание слайда:

Тела вращения *

2 слайд

Описание слайда:

Цилиндр. Площади поверхностей и объем цилиндра. Цилиндром называется геометрическая фигура полученная при вращении прямоугольника вокруг из его сторон. Сторона вокруг которой вращается прямоугольник называется осью симметрии, осью вращения и высотой цилиндра. Другая сторона прямоугольника параллельная стороне – оси вращения, при вращении образует цилиндрическую поверхность и называется образующей цилиндра. Две другие параллельные стороны прямоугольника при вращении образуют круги – основания цилиндра и называются радиусами оснований. OO — ось вращения, ось симметрии, высота AA =BB – образующая цилиндра AO= A O –радиус основания * A A B B O O 1 1 1 1 1 1

3 слайд

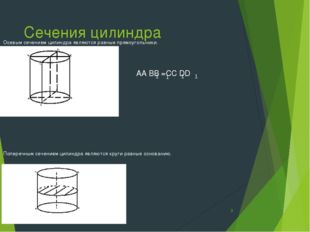
Описание слайда:

Сечения цилиндра Осевым сечением цилиндра являются равные прямоугольники. AA BB =CC DD Поперечным сечением цилиндра являются круги равные основанию. * 1 1 1 1

4 слайд

Описание слайда:

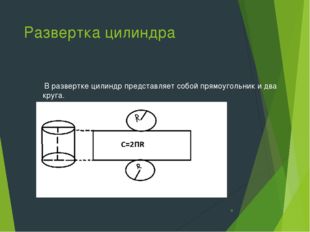
Развертка цилиндра В развертке цилиндр представляет собой прямоугольник и два круга. *

5 слайд

Описание слайда:

Площади поверхности и объем цилиндра * Sп.п=2ПR(h +R)- Площадь полной поверхности цилиндра Sб.п=2*П*R*h-Площадь боковой поверхности цилиндра, где R — радиус, h — высота, l — образующая Vц=So*h=П*R*h — Объем цилиндра

6 слайд

Описание слайда:

Конус. Площади поверхностей и объем конуса. SO — ось вращения, ось симметрии, высота AO=OB – радиус основания SA=SB — образующие * O S A B

7 слайд

Описание слайда:

Сечения конуса Осевым сечением конуса является множество равных равнобедренных треугольников. SAB= SCD=… * O C B A D S

8 слайд

Описание слайда:

Развертка конуса В развертке конус представляет собой круговой сектор и круг. *

9 слайд

Описание слайда:

Площади поверхностей и объем конуса Sб. п. = П*R*l- площадь боковой поверхности конуса Sп. п. =П*R*(l*R)- — площадь полной поверхности конуса 2 Vк =1/3*So*h= 1/3 П*R*h — объем конуса *

10 слайд

Описание слайда:

Усеченный конус. Площади поверхностей и объем конуса Усеченным конусом называется геометрическая фигура, полученная при вращении прямоугольной трапеции вокруг боковой стороны перпендикулярной основанию. Сторона вокруг которой вращается прямоугольная трапеция называется осью вращения, осью симметрии и высотой усеченного конуса. Другая боковая сторона трапеции не перпендикулярная основаниям, образует при вращении коническую поверхность и называется образующей усеченного конуса. Основания трапеции при вращении образуют круги – основания усеченного конуса и называются радиусами оснований. Усеченным конусом называется часть конуса, заключенная между основанием конуса и плоскостью параллельной основанию. OO – ось вращения, ось симметрии и высота AA =BB — образующая AO=BO – радиус нижнего основания A O =B O –радиус верхнего основания * 1 1 1 1

11 слайд

Описание слайда:

Сечения усеченного конуса Осевым сечением усеченного конуса является множество равных равнобедренных трапеций. *

12 слайд

Описание слайда:

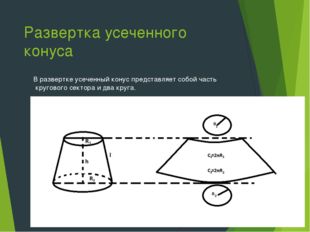
Развертка усеченного конуса В развертке усеченный конус представляет собой часть кругового сектора и два круга. *

13 слайд

Описание слайда:

Площади поверхности и объем конуса. * -Площадь боковой поверхности усеченного конуса, где l-образующая,R и R –радиусы оснований 1 2 Площадь полной поверхности усеченного конуса, где R и R — радиусы оснований 1 2 — Объем усеченного конуса

14 слайд

Описание слайда:

Сфера и шар. Касательная плоскость к сфере. Площади поверхности и объем шара Сферой (шаровой поверхностью) называется множество точек пространства равноудаленных от данной точки. Сферой называется геометрическая фигура полученная при вращении полуокружностей вокруг её диаметра. Радиусом сферы называется отрезок соединяющий центр сферы с любой её точкой. Хордой сферы называется отрезок соединяющий две её любые точки. Диаметром сферы называется хорда проходящая через центр сферы. O – центр сферы AO=OB=OC=OD – радиус AB=CD –диаметр AC — хорда *

15 слайд

Описание слайда:

Теоремы Теорема 1: Сечение сферы плоскостью, есть окружность. Касательной плоскостью к сфере называется плоскость имеющая со сферой только одну общую точку. Теорема 2: Плоскость перпендикулярная к радиусу в его конце лежащем на сфере, есть касательная плоскость. *

16 слайд

Описание слайда:

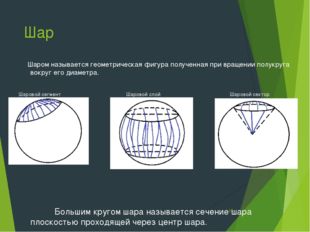
Шар Шаром называется геометрическая фигура полученная при вращении полукруга вокруг его диаметра. Шаровой сегмент Шаровой слой Шаровой сектор Большим кругом шара называется сечение шара плоскостью проходящей через центр шара. *

17 слайд

Описание слайда:

Площади поверхностей и объем шара -Площадь поверхности шара -Объем шара *

Курс повышения квалификации

Курс повышения квалификации

Курс профессиональной переподготовки

Учитель математики и информатики

Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:

Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое

Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс

Выберите учебник:
Все учебники

Выберите тему:
Все темы

также Вы можете выбрать тип материала:

Общая информация

Номер материала:

ДБ-025176

Похожие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Что такое развертка конуса и как ее построить? Формулы и пример решения задачи

Каждый школьник слышал о круглом конусе и представляет, как выглядит эта объемная фигура. В данной статье дается определение развертки конуса, приводятся формулы, описывающие ее характеристики, а также описывается способ ее построения с помощью циркуля, транспортира и линейки.

Круглый конус в геометрии

Приведем геометрическое определение этой фигуры. Круглым конусом называется поверхность, которая образована прямыми отрезками, соединяющими все точки некоторой окружности с одной-единственной точкой пространства. Эта единственная точка не должна принадлежать плоскости, в которой лежит окружность. Если вместо окружности взять круг, то указанный способ также приводит к получению конуса.

Круг называется основанием фигуры, его окружность — это директриса. Отрезки, соединяющие точку с директрисой, называются генератрисами или образующими, а точка, где они пересекаются — это вершина конуса.

Круглый конус может быть прямым и наклонным. Обе фигуры показаны ниже на рисунке.

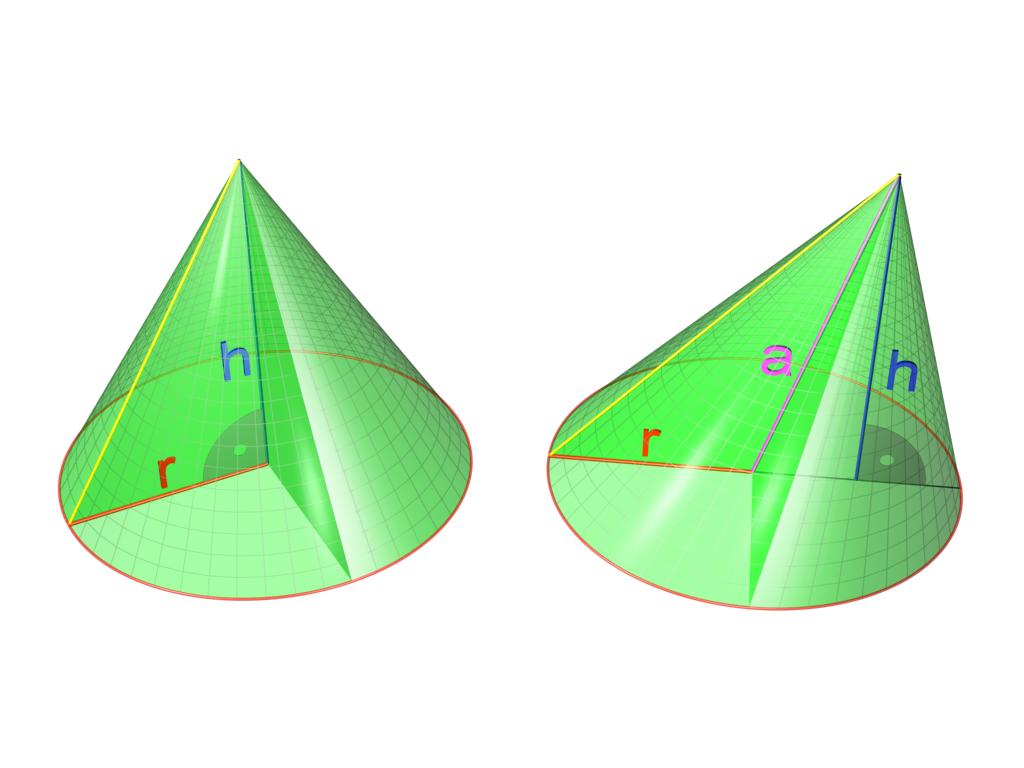
Разница между ними заключается в следующем: если перпендикуляр из вершины конуса падает точно в центр окружности, то конус будет прямым. Для него перпендикуляр, который называется высотой фигуры, является частью его оси. В случае конуса наклонного высота и ось образуют некоторый острый угол.

Ввиду простоты и симметричности фигуры далее будем рассматривать свойства только прямого конуса с круглым основанием.

Получение фигуры с помощью вращения

Перед тем как перейти к рассмотрению развертки поверхности конуса, полезно узнать, как с помощью вращения можно получить эту пространственную фигуру.

Предположим, что у нас имеется прямоугольный треугольник со сторонами a, b, c. Первые две из них являются катетами, c — это гипотенуза. Поставим треугольник на катет a и начнем его вращать вокруг катета b. Гипотенуза c при этом опишет коническую поверхность. Эта простая методика получения конуса изображена ниже на схеме.

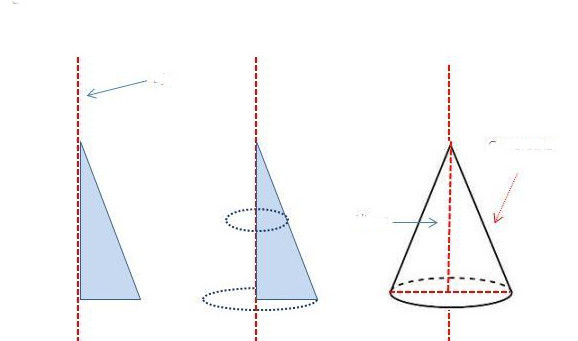
Очевидно, что катет a будет радиусом основания фигуры, катет b — его высотой, а гипотенуза c соответствует образующей круглого прямого конуса.

Вид развертки конуса

Как можно догадаться, конус образован двумя типами поверхностей. Одна из них — это плоский круг основания. Предположим, что он имеет радиус r. Вторая поверхность является боковой и называется конической. Пусть ее образующая будет равна g.

Если у нас имеется бумажный конус, то можно взять ножницы и отрезать от него основание. Затем, коническую поверхность следует разрезать вдоль любой образующей и развернуть ее на плоскости. Таким способом мы получили развертку боковой поверхности конуса. Две поверхности вместе с исходным конусом показаны на схеме ниже.

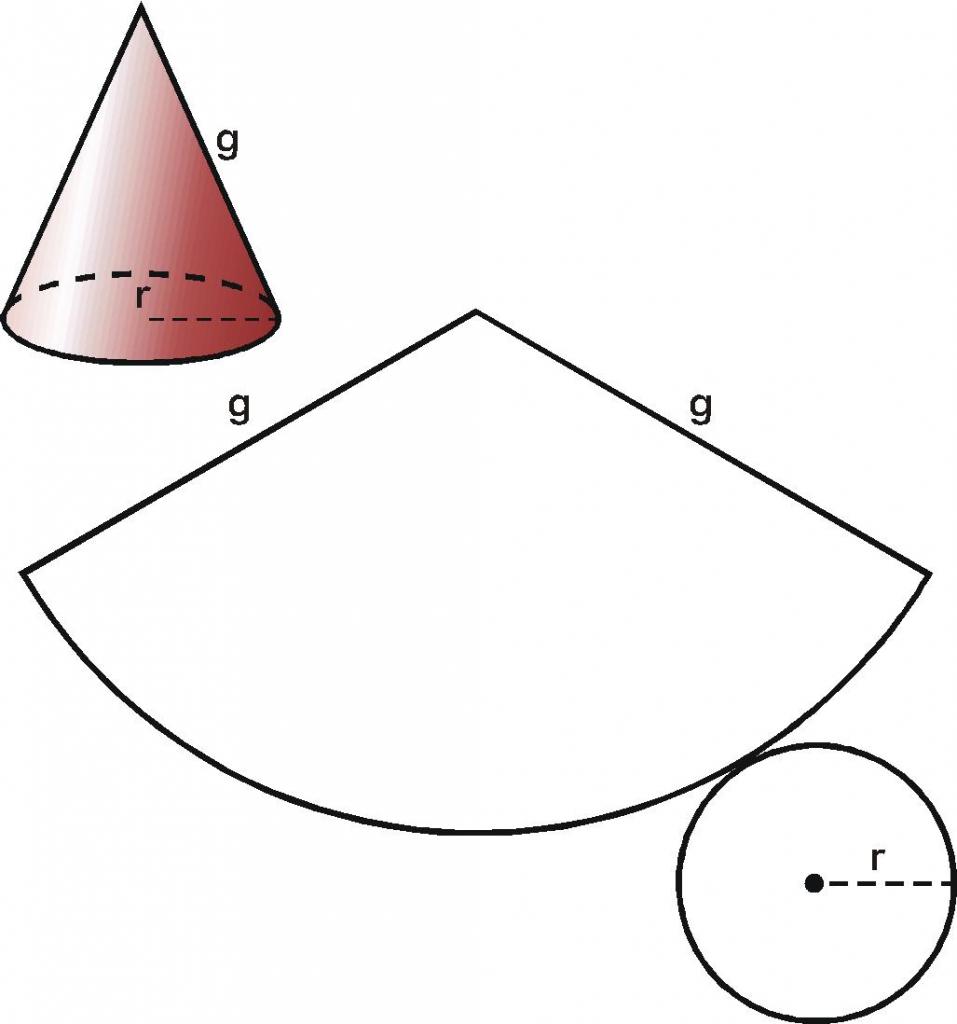
Внизу справа изображен круг основания. По центру показана развернутая коническая поверхность. Оказывается, что она соответствует некоторому круговому сектору круга, радиус которого равен длине образующей g.

Угол и площадь развертки

Теперь получим формулы, которые по известным параметрам g и r позволяют рассчитать площадь и угол развертки конуса.

Очевидно, что дуга кругового сектора, показанного выше на рисунке, имеет длину, равную длине окружности основания, то есть:

l = 2*pi*r.

Если бы весь круг радиусом g был построен, то его бы длина составила:

L = 2*pi*g.

Поскольку длина L соответствует 2*pi радианам, тогда угол, на который опирается дуга l, можно определить из соответствующей пропорции:

L ==> 2*pi;

l ==> φ.

Тогда неизвестный угол φ будет равен:

φ = 2*pi*l/L.

Подставляя выражения для длин l и L, приходим к формуле для угла развертки боковой поверхности конуса:

φ = 2*pi*r/g.

Угол φ здесь выражен в радианах.

Для определения площади S_b кругового сектора воспользуемся найденным значением φ. Составляем еще одну пропорцию, только уже для площадей. Имеем:

2*pi ==> pi*g²;

φ ==> S_b.

Откуда следует выразить S_b, а затем, подставить значение угла φ. Получаем:

S_b = φ*g²*pi/(2*pi) = 2*pi*r/g*g²/2 = pi*r*g.

Для площади конической поверхности мы получили достаточно компактную формулу. Величина S_b равна произведению трех множителей: числа пи, радиуса фигуры и ее образующей.

Тогда площадь всей поверхности фигуры будет равна сумме S_b и S_o (площадь круглого основания). Получаем формулу:

S = S_b + S_o = pi*r*(g + r).

Построение развертки конуса на бумаге

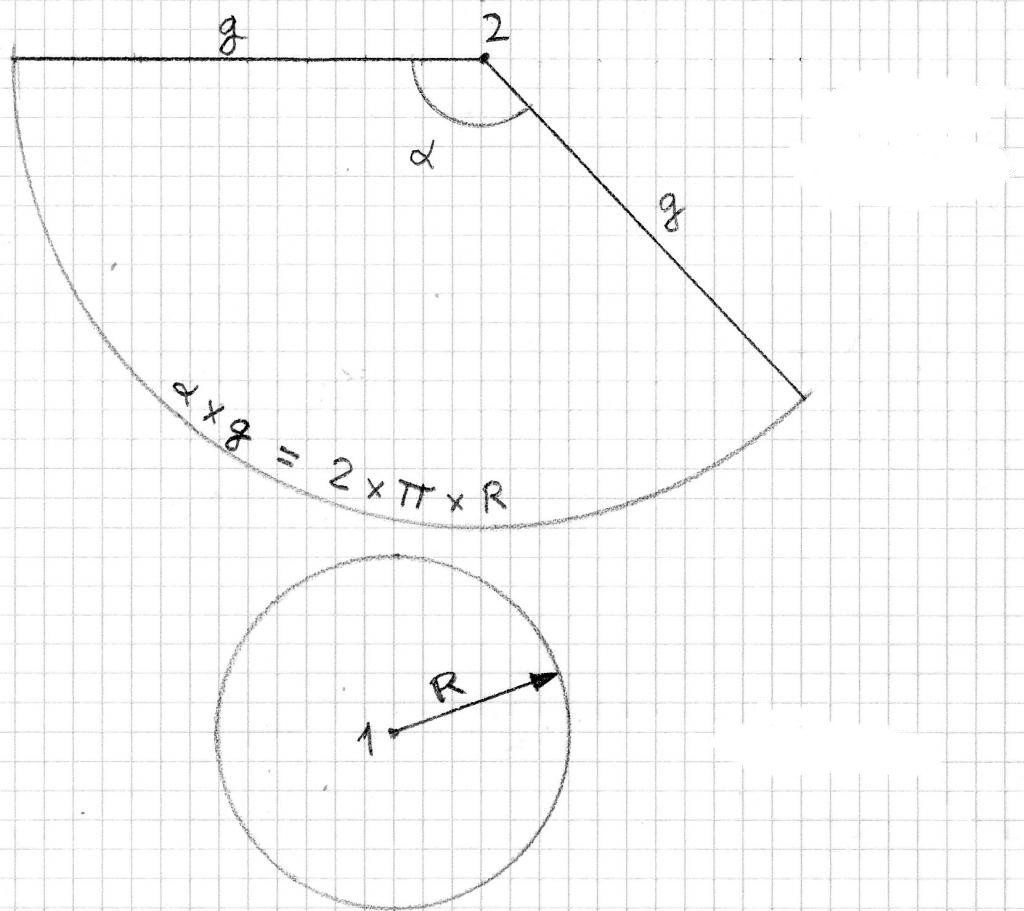
Для выполнения этой задачи понадобится лист бумаги, карандаш, транспортир, линейка и циркуль.

В первую очередь начертим прямоугольный треугольник со сторонами 3 см, 4 см и 5 см. Его вращение вокруг катета в 3 см даст искомый конус. У фигуры r = 3 см, h = 4 см, g = 5 см.

Построение развертки начнем с рисования циркулем окружности радиусом r. Ее длина будет равна 6*pi см. Теперь рядом с ней нарисуем еще одну окружность, но уже радиусом g. Ее длина будет соответствовать 10*pi см. Теперь нам нужно от большой окружности отрезать круговой сектор. Его угол φ равен:

φ = 2*pi*r/g = 2*pi*3/5 = 216^o.

Теперь откладываем транспортиром этот угол на окружности с радиусом g и проводим два радиуса, которые будут ограничивать круговой сектор.

Таким образом, мы построили развертку конуса с указанными параметрами радиуса, высоты и образующей.

Пример решения геометрической задачи

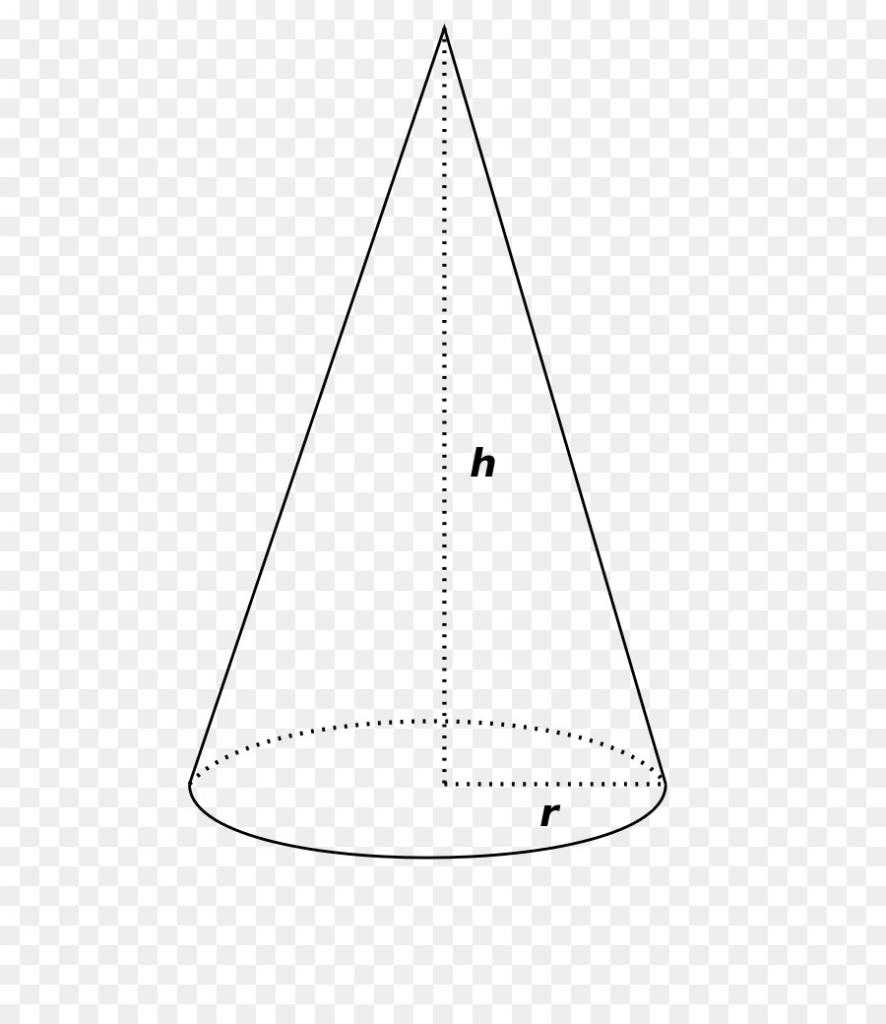
Дан круглый прямой конус. Известно, что угол его боковой развертки равен 120^o. Необходимо найти радиус и образующую этой фигуры, если известно, что высота h конуса равна 10 см.

Задача не является сложной, если вспомнить, что круглый конус — это фигура вращения прямоугольного треугольника. Из этого треугольника следует однозначная связь между высотой, радиусом и образующей. Запишем соответствующую формулу:

g² = h² + r².

Вторым выражением, которое следует использовать при решении, является формула для угла φ:

φ = 2*pi*r/g.

Таким образом, мы имеем два уравнения, связывающих две неизвестные величины (r и g).

Выражаем из второй формулы g и подставляем результат в первую, получаем:

g = 2*pi*r/φ;

h² + r² = 4*pi²*r²/φ² =>

r = h /√(4*pi²/φ² — 1).

Угол φ = 120^o в радианах равен 2*pi/3. Подставляем это значение, получаем конечные формулы для r и g:

r = h /√8;

g =3*h /√8.

Остается подставить значение высоты и получить ответ на вопрос задачи: r ≈ 3,54 см, g ≈ 10,61 см.

Трапеция

(Перейти к области трапеции или периметру трапеции)

Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, имеющая пару противоположных сторон, параллельных (отмечены стрелками ниже):

Трапеция		Равнобедренная трапеция

Трапеция:

	имеет пару параллельных сторон
	— это равнобедренная трапеция , когда она имеет равных углов с параллельной стороны
	называется « трапеция » в Великобритании (см. Ниже)

Люфт трапецией:

Параллельные стороны — это «основания»

Две другие стороны — «ножки»

Расстояние (под прямым углом) от одной базы до другой называется «высотой»

Площадь
трапеции

Площадь — это среднее значение для двух базовых длин, в раз превышающее высоту : Площадь = a + b 2 × h

Пример: два основания трапеции 6 м и 4 м, а высота 3 м.Какова его площадь?

Площадь = 6 м + 4 м 2 × 3 м = 5 м × 3 м = 15 м ²

Инструмент «Площадь многоугольника путем рисования» полезен, когда вы можете нарисовать трапецию.

Периметр трапеции

Периметр — это расстояние по краям.

Периметр — сумма длин всех сторон : Периметр = a + b + c + d

Пример: Трапеция имеет длину стороны 5 см, 12 см, 4 см и 15 см. Каков ее периметр?

Периметр = 5 см + 12 см + 4 см + 15 см = 36 см

Медиана трапеции

Медиана (также называемая средней линией или промежуточным сегментом) — это линейный сегмент на полпути между двумя основаниями. Средняя длина — это среднее значение двух базовых длин: м = а + б 2

Вы можете рассчитать площадь, зная медианное значение, это просто медиана, умноженная на высоту:

Площадь = mh

Трапеция

Трапеция (UK: trapezoid) — четырехугольник без параллельных сторон.

Определения США и Великобритании поменялись местами, например:

	Трапеция	Трапеция
США:	Пара параллельных сторон	НЕТ параллельных сторон
Великобритания:	НЕТ параллельных сторон	Пара параллельных сторон

,

Трапеция — определение математического слова

Трапеция — определение математического слова — Math Open Reference

Четырехугольник, у которого есть хотя бы одна пара параллельных сторон

(но см. Примечания к определениям ниже)

Попробуйте это Перетащите оранжевые точки на каждую вершину
изменить форму фигуры. Обратите внимание, что стороны AB и CD остаются параллельными.

Атрибуты

База	Одна из параллельных сторон. Каждая трапеция имеет два основания. Видеть Базовые определения.
Нога	Стороны AC и BD выше называются сторонами трапеции и обычно не параллельны, хотя они могут быть (см. примечание о параллелограмме ниже). У каждой трапеции две ножки.
Высота	Высота трапеции равна расстояние по перпендикуляру от одной базы до другой. (Возможно, потребуется расширить одну базу).
Медиана	Медиана трапеции — это линия, соединяющая середины двух ног.См. Медиана трапеции
Площадь	Обычный способ вычисления площади — это средняя длина основания, умноженная на высоту. Увидеть площадь трапеции
Периметр	Расстояние вокруг трапеции. Сумма длин его сторон. Увидеть периметр трапеции

Если обе ноги имеют одинаковую длину, это называется равнобедренной трапецией , и оба базовых угла одинаковы.

Если ноги параллельны, то теперь у него две пары параллельных сторон, и это параллелограмм.

Координатная геометрия

В координатной геометрии, если вы знаете координаты четырех вершин,
вы можете рассчитать различные его свойства, включая высоту и медианное значение.
Подробнее об этом см. Определение трапеции (координатная геометрия).

Примечания к определениям

Существует значительная путаница с определениями «трапеция» и «трапеция» из-за различий в британской и американской версиях.
Как видно из таблицы ниже, значения этих двух слов в американской и британской интерпретациях полностью противоположны.

	Британский	США
Трапеция	Четырехугольник без параллельных сторон	Четырехугольник с одной парой параллельных сторон
Трапеция	Четырехугольник с одной парой параллельных сторон	Четырехугольник без параллельных сторон

Другие полигоны

Общие

Типы многоугольника

Площадь различных типов полигонов

Периметр различных типов полигонов

Углы, связанные с многоугольниками

Именованные полигоны

(C) Открытый справочник по математике, 2011 г.
Все права защищены.

,

Свойства трапеции

Определения и формулы для периметра трапеции, площади трапеции, свойств сторон и углов трапеции, свойств сторон и углов равнобедренной трапеции
Просто прокрутите вниз или нажмите на то, что вы хотите, и я прокручу для вас!

Периметр трапеции:
	Чтобы найти периметр трапеции, просто сложите все длины сторон: Периметр = a + b + c + B

Площадь трапеции:
	Найти площадь трапеции… Более длинное основание (нижнее) — это большая B, а меньшее основание (верхнее) — это маленькая b …
Да, вот формула … Но давайте посмотрим, откуда она взялась!

Возьмите две копии трапеции (одну синюю трапецию и одну зеленую трапецию) … Переверните одну вверх ногами и склейте их вместе … Теперь у вас есть параллелограмм. Площадь параллелограмма = основание x высота = (B + b) x h Но это вдвое больше, чем нам нужно… Итак, умножаем на 1/2!

,

Как определить объем трехмерной трапеции?

Геометрия

Наука

• Анатомия и физиология

• астрономия

• астрофизика

• Биология

• Химия

• наука о планете Земля

• Наука об окружающей среде

• Органическая химия

• физика

математический

• Алгебра

• Исчисление

.