Презентация фигурки из кубиков и их частей 6 класс: «ФИГУРКИ ИЗ КУБИКОВ И ИХ ЧАСТЕЙ 6 класс. МЕТОД ТРЁХ ПРОЕКЦИЙ Определите, где изображён вид детали сверху, вид спереди и вид слева.». Скачать бесплатно и без регистрации.

Презентация к уроку «Куб» — математика, презентации

Тема: Задачи на проекционном чертеже

Цель: познакомить учащихся с методом трёх проекций как одним из способов изображения пространственных фигур на плоскости.

Задачи: повторить элементы куба; дать понятия кратчайшего расстояния; познакомить учащихся с изображением пространственных тел на плоскости; развивать пространственное воображение; учить работе в парах; учить самооценке и взаимооценке.

Ход урока

1. Организация начала урока

Здравствуйте! Сегодня на уроке мы расширим знания об уже известном нам многограннике. А о каком многограннике пойдёт речь, вы узнаете, ответив на вопрос: как называется правильный шестигранник, все грани которого квадраты? Каждый из вас умён и не глуп, чётко знает это (куб).

На доске записаны термины, с которыми мы встретимся сегодня на уроке. С какими из них вы не знакомы? Дайте им определение. Насколько вы правы,мы узнаем в конце урока.

На доске: ребро, вершина, грань, развертка, кратчайшее расстояние, проекция, кубизм

II Актуализация знаний учащихся. Повторение изученного материала.

Запишем тему урока. Куб.

1. Постройте в тетради куб. Для тех, кто забыл, как строится куб подсказка на слайде.
2. Фронтальный опрос.

1. Назовите элемент куба, который является четырехугольником? (Грань)
2. Сколько граней у куба? (6)
3. Назовите элемент куба, который является отрезком. (Ребро)
4. Сколько рёбер у куба? (12)
5. Как называют концы рёбер? (вершина)
6. Сколько вершин у куба? (8)
7. Сколько ребер сходится в одной вершине? (3)
8. Сколько соседних граней имеет каждая грань? (4)
9. Сколько ребер имеет одна грань? (4)

1. Решим задачу о Пауке и Мухе: в противоположных вершинах куба сидят Паук и Муха. Каким кратчайшим путем Паук может доползти до Мухи? Покажите этот путь на модели куба. Рассмотрим ваше решение на развёртке куба. Отметим точками паука и муху. Изобразите кратчайшее расстояние. Что увидели?
2. Задачи на развёртках

Развертки имеют большое применение на машиностроительных заводах, обувных фабриках, в швейных мастерских. Каждый из нас ежедневно использует вещи, изготовленные по их разверткам, т.е. выкройкам. Это платья, блузы, брюки, обувь, сумки, портфели и многое другое. По разверткам делают спортивные мячи воздушные змеи и шары, паруса яхт, упаковки для бытовой техники, подарочных наборов и т.д. От надежности и удобства упаковки зависит качество транспортировки изделия, а от красоты ее дизайна, т.е. формы, графики, цвета зависит выбор товара покупателем.

Задача. В нужном месте лицевой стороны развертки куба запишите в правильном расположении буквы Г и Р (даны виды разверток с буквами)

1. Физминутка.

А теперь все тихо встали,

Дружно руки вверх подняли,

В стороны, вперёд, назад,

Повернулись вправо, влево

•  сели, вновь за дело.

1. Изучение нового материала.

Изображение пространственного тела на плоскости — дело непростое. Ведь надо нарисовать его, чтобы ясно было, как оно выглядит со всех сторон. Для облегчения этой задачи изобрели метод трёх проекций. Этим методом пользуются чертёжники, инженеры, рабочие для изображения и изготовления различных деталей. В чём состоит метод трёх проекций? Мы смотрим на тело с трёх сторон: спереди, сверху и слева. Затем делаем три чертежа, изображающих увиденное.

III. Практическая работа (прямая задача)

Сложите фигуры из кубиков. Дорисуй их проекции. а-в) работа у доскиГ) самостоятельно. Взаимопроверка.

По данным проекциям фигуры сложи её из кубиков (обратная задача)

IV. Познавательный материал.

1. В начале 20 века зародилось такое направление в искусстве как кубизм. Оно характеризуется использованием геометрических форм и дробление реальных объектов на стереометрические примитивы.

2. V. Итог урока. Домашнее задание. 1) По рисункам выполни их проекции. 2) Рисунок в стиле кубизма.

Просмотр содержимого документа

«презентация к уроку «Куб» »

Методическая разработка по алгебре (5 класс) на тему: Программа кружка « Наглядная геометрия», 5-6 класс, в рамках реализации ФГОС

Занятие внеурочной деятельности. Презентация. «Задачи на разрезание и складывание фигур».

Открытое занятие по внеурочной деятельности

в 6 классе.

Тема: Задачи на разрезание и складывание фигур.

Форма занятия: решение практических задач

Цели:

Обучающая:

• активизировать мыслительную деятельность учащихся посредством участия каждого из них в процессе работы;

• показать, какие качества необходимы при изучении математики;

Развивающая:

• развитие познавательного интереса к геометрии;

• развитие логического мышления, быстроты реакции, внимания.

Воспитывающая:

Планируемый результат обучения, в том числе и формирование УУД:

-формировать вычислительные навыки;

-совершенствовать умение решать логические задачи, задачи на разрезание;

-способствовать развитию творческих способностей.

формирование у учащихся практических умений и навыков при разрезании и складывании геометрических фигур.

Формируемые УУД:

Познавательные:

-совершенствовать вычислительные навыки,

-совершенствовать умение решать текстовые и геометрические задачи;

Коммуникативные:

-формировать умение работать в группе, находить общее решение, умение аргументировать и отстаивать своё предложение;

-развивать способность сохранять доброжелательное отношение друг к другу, взаимоконтроль и взаимопомощь по ходу выполнения задания;

Регулятивные:

-проявлять познавательную инициативу в учебном сотрудничестве.

Личностные:

-формировать способности к самооценке на основе критериев успешности учебной деятельности.
Используемые технологии: групповая, ИКТ.

Занятие рассчитано на класс со средним уровнем знания математики; продолжительность занятия 30-35 минут.

Учитель математики и физики первой категории: Легомина Людмила Владимировна

1. Адаптационный этап(Эмоциональный настрой)

1) Организационный момент.

Вас приветствую, друзья!

Посмотрите на меня.

Спинку ровненько держите,

Руки вместе положите.

Начинается урок.

У нас сегодня присутствуют гости. Поприветствуем их.

Улыбнитесь друг другу.

— Я рада приветствовать Вас на занятии кружка, присаживайтесь.

Садятся за парты.

2.Актуализация знаний.

2) Постановка проблемы

«Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» — говорил Галилео Галилей(Слайд №1)

Начнем мы сегодня занятие со слов Г. Галилея, великого итальянского ученого, физика, который является первым экспериментатором, открыл очень много законов, в том числе и закон Инерции.

-Ребята, а кто мне скажет, что означают эти слова?

-Какие качества необходимы при изучении математики и геометрии?

Действительно, смекалка и находчивость, усидчивость и аккуратность при выполнении заданий помогут вам сегодня в достижении цели.

А какие задания вы будете выполнять, чем вы будете заниматься на уроке, вы узнаете, выполнив небольшую практическую работу №1: «Разрежь торт», «Собери квадрат». Работать будете парами.

(Слайд 2)(разрезание торта)

Итак, кто догадался, чем мы будем заниматься на уроке?

Откройте тетради, запишите тему занятия.

(Слайд №3)Задачи на разрезание и складывание фигур.

— дети читают на экране слова

Г. Галилея

— ребята дают свои ответы…

(правильно мыслить и рассуждать)…

— дети называют качества…. (сообразительность, усидчивость,внимательность, умение мыслить, рассуждать, быстро считать, память, наблюдательность, аккуратность и т.д.)

Работают парами, обсуждают решение, разрезают торт, собирают квадрат.

На доске проверяем. (один учащийся выходит и показывает собранный квадрат)

Ребята отвечают …..

—разрезать и собирать фигуры,

— открывают тетради, записывают тему урока «Задачи на разрезание и складывание фигур».

3.Основной этап.

А сейчас проведем небольшую разминку.

Решим задачу на первое качество –внимание (записать на доске !!)

1. Внимание

Кирпич весит 2 кг и еще треть своего собственного веса.

Сколько весит кирпич? (Слайд №4). Ответ:(Слайд №5)

2. Умение быстро считать(Слайд №6) (про лилии)

3. Воображение

Отметьте на сторонах прямоугольника восемь точек так, чтобы на каждой стороне было по три точки.

Ответ: (Слайд №7- №8)

4. Наблюдательность(Слайд №9, №10)

Какую фигуру вы нарисовали бы следующей?

Ответ:шестиугольник.

Итак, ребята наша разминка закончилась, начинаем решать задачи на разрезание (Слайд №11).

Будем работать группами по три человека, задание выполняем аккуратно, соблюдая правила работы в группе. Выберите ответственного, кто будет представлять решение.

5. Аккуратность (Слайд №11). (Решение задач)

Умение работать в команде.

Задание на разрезание (раздает карточки)

(Слайд №12-№15).

Слайд №16 для учителей

Задачи на складывание фигур

(Слайд №17- №20)

Каждая группа собирает свой квадрат.

Затем свое решение прикрепляет магнитиками на доске

Дать задание и присутствующим — 5 группа)

(Слайд №21)

6. Умение получать удовольствие от того, что делаешь сам

Мы с вами собирали квадраты из пяти различных фигур.

В умелых руках обыкновенный квадрат становится удивительной фигурой: он может быть превращен в другую фигуру или в несколько других фигур, имеющих порой занимательную форму. Несколько тысяч лет тому назад, китайский учёный ТАНГ, предложил разделить квадрат остроумным способом на 7 частей.

(Слайд № 26-№27).

А сейчас я вам предлагаю выполнить проект: из волшебного квадрата, (Слайд №28) сложить фигуру и придумать название вашей фигуры, проекта.

(Слайд №29- №30)- (предполагаемые проекты)

— учащийся записывает первое качество на доске.

— ребята устно решают задачу на внимание.

-обсуждаем решение и приходим к соглашению.

— устно решают задачу.

— ребята в тетрадях изображают прямоугольник и рисуют восемь точек

— разбирают решение задачи и проверяют с решением на доске (презентация)

(Слайд №8)

—

— ребята в тетради рисуют предполагаемую фигуру

проверяют решение

(презентация) (Слайд№10)

— ребята работают в группе по три человека (три парты)

— думают над задачей, решение групп вывешивают на доску и сверяют с решением на слайде (№12,№13,№14,№15)

— ребята работают в группе по три человека (три парты)

— думают над задачей, решение групп вывешивают на доску и сверяют с решением на слайде

(Слайд №21)

— ребята работают в группе по четыре человека (две парты)

— головоломка ТАНГРАМ раздаётся каждой группе

— складывают фигуру из частей квадрата и придумывают название картинки

— обсуждают и проверяют

— определяют победителя (хлопаем в ладоши)

—

4. Итог урока

Подведём итог занятия

Кто скажет, что нового вы узнали на этом занятии?

Чему научились на уроке?

Какие качества математики вам пригодились для достижения цели?

Где могут пригодиться ваши знания?

Вы можете сами придумывать такие задания на разрезание и складывание фигур, решать на переменках, дома, в дороге, на природе.

— ребята говорят о качествах математики (прочитать запись на доске), о решении задач на разрезание

5. Рефлексия

Оцените сегодняшний урок. Втабличке, лежащей на столахотметьте «галочкой» в соответствующей графе.

в картинках и текстовые, для взрослых и детей

Задача Фибоначчи о размножении кроликов

Леонардо Пизанский (около 1170 г.р.), по прозвищу Фибоначчи, — один из первых именитых математиков средневековой Европы. Он успешно участвовал в математических турнирах, а, создав себе имя, придумывал для них занимательные задачи. Ниже одна из самых известных.

«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца.
Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов».

Сколько пар кроликов будет в огороженном месте через 12 месяцев с начала размножения?

Подсказка Вспомните последовательность Фибоначчи или запаситесь терпением — и считайте.

Задача Тартальи «Трудное наследство»

Никколо Тарталья (1499 г.р.), итальянский математик, обнаруживший общий алгоритм решения кубических уравнений. Описанный Никколо метод вошел в историю математики как Формула Кардано, по имени первого публикатора метода, до которого независимо друг от друга додумались Тарталья и Сципион дель Ферро.

Предлагаем решить ставшую известной задачу Тартальи о дележе лошадей.

Как выполнить завещание?

Головоломка Льюиса Кэрролла

Известный писатель Льюис Кэрролл, тот самый, который создал истории об Алисе и ее приключениях в Стране Чудес и Зазеркалье, еще и очень любил придумывать головоломки и преподавал логику.

Своим маленьким поклонникам Кэрролл часто предлагал такую головоломку:

Задача усложняется особыми условиями ее выполнения:

• карандаш от бумаги отрывать нельзя;
• дважды проводить карандашом в одном месте нельзя;
• пересекать линии нельзя.

Презентации PowerPoint для 6 классов — 1-й квартал

Доброго времени суток, товарищи учителя. Доступны более презентаций PowerPoint для 6 класса — 1 квартал . Спасибо всем нашим создателям файлов, участникам и редакторам файлов за то, что они поделились этими файлами. Скоро будут загружены другие файлы. Спасибо!

>>> PowerPoint экономит время и силы. После того, как презентация создана, ее легко обновить и изменить для других уроков. Он портативный, и им можно легко поделиться со студентами и коллегами.Он также поддерживает мультимедиа, такую ​​как видео, аудио, изображения и анимацию.

Преимущества презентаций PowerPoint

Презентации PowerPoint производят лучшие визуальные эффекты и более глубокое впечатление. Содержание научных лекций часто абстрактно, иногда их трудно объяснить с помощью классной доски. Однако, представляя слайды PowerPoint с изображениями, блок-схемами, схемами, анимацией и даже видеоклипами, лекция может стать яркой и привлекательной для студентов.

PowerPoint Presentations ускоряет передачу информации. В презентации PowerPoint учитель может передать больше информации, чем на традиционной лекции. Объем информации, передаваемой на традиционной лекции, часто ограничивается скоростью написания инструктором на доске. Но в презентации PowerPoint все схемы были напечатаны ранее на слайдах. Особенно, когда при обучении на курсах естествознания необходимо представить большой объем данных, использование PowerPoint может значительно повысить эффективность лекции.По сравнению с написанием классной доски в традиционной лекции файл PowerPoint можно легко копировать, поддерживать, передавать и распечатывать.

Для учащихся файл может быть доступен в Интернете до или после урока, и поэтому его можно предварительно просмотреть или просмотреть. Это может быть самая ценная функция PowerPoint. Презентация PowerPoint экономит время для учащихся, у которых различия в обучении требуют больше времени для заметок, поскольку они могут загружать файлы PowerPoint из Интернета и получать организованные заметки или раздаточные материалы и точно нарисованные графики.Таким образом, PowerPoint может повысить успеваемость учащихся в классе.

PowerPoint Presentations более точны и систематичны. Хорошо подготовленный PowerPoint может представить учащимся более точное содержание тем. Перед презентацией, отредактировав или просмотрев файл PowerPoint, учитель имеет достаточно времени, чтобы проверить написание термина, выражение концепции или теории, логичность вывода формулы, а также точность чисел и данных и т. Д. Для учащихся это необходим для правильного и точного понимания темы.После занятий, собрав отзывы студентов, учитель мог легко оптимизировать слайды PowerPoint, чтобы они соответствовали студентам, редактируя слайды. С другой стороны, слайды PowerPoint могут быть систематизированы. Четкий план может быть полезен учащимся для построения правильных знаний. <<<

.

6 класс Математика Модуль 5, Тема C, Обзор

6 класс Математика Модуль 5, Тема C, Обзор

В 5-м классе ученики распознали объем как атрибут сплошных фигур. Они измерили объем, упаковав прямоугольные призмы единичными кубами, и обнаружили, что определение объема было таким же, как и умножение длин краев призмы ( 5.MD.C.3 , 5.MD.C.4 ). Студенты распространяют эти знания на тему C, где они продолжают упаковывать прямоугольные призмы единичными кубами; однако на этот раз правая прямоугольная призма имеет дробные длины ( 6.G.A.2 ). В Уроке 11 учащиеся разбирают призму с одним кубом, чтобы концептуализировать нахождение объема правой прямоугольной призмы с дробными длинами ребер с использованием единичных кубов. Они соединяют эти выводы, чтобы применить формулу V = lwh и умножить дробные длины кромок ( 5.NF.B.4 ). На уроках 12 и 13 ученики расширяют и применяют формулу объема к V = Площадь основания умножить на высоту или просто V = bh , где b представляет площадь основания. В Уроке 12 учащиеся изучают основания правильных прямоугольных призм и сначала находят площадь основания, а затем умножают ее на высоту. Они определяют, что две формулы могут быть использованы для определения объема правой прямоугольной призмы. В Уроке 13 учащиеся применяют обе формулы к прикладным задачам.Тема C завершается практическим применением формулы объема, где учащиеся расширяют понятие, что объем является аддитивным ( 5.MD.C.5c ), и находят объем составных твердых фигур. Они применяют формулы объема и используют свой предыдущий опыт решения уравнений ( 6.EE.B.7 ), чтобы найти недостающие объемы и недостающие размеры.

.

Объем кубов и прямоугольных призм — класс 6

Разблокируйте более сложные уровни, набрав в среднем 80% или выше.

Зарабатывайте до 5 звезд за каждый уровень
Чем больше вопросов вы ответите правильно, тем больше звезд вы получите!

В каждой игре по 10 вопросов.
Зеленый прямоугольник означает правильный.
Желтое поле означает неправильное.

Другие способы использования математических игр

Поделитесь этим навыком со своими учениками

Поделиться в Google Classroom

Создайте задание класса Google, которое позволяет учащимся создавать и заполнять свои собственные рабочие листы

Поделиться напомнить

Поделитесь со своими учениками в Напоминании, чтобы они могли создавать свои собственные рабочие листы

Создать задание MathGames

Создайте задание MathGames, используя учетную запись родителя или учителя для ученика в MathGames.

Создать тест MathGames

Узнайте, на каком уровне находятся ваши ученики, с детальной оценкой уровня их навыков.

Скопируйте эту ссылку в свой план урока напрямую

http: // www.mathgames.com/skill/6.124-volume-of-cubes-and-rectangular-prisms

Эта ссылка ведет непосредственно к этому навыку, учетные записи студентов не требуются.

.

11-1 Космические фигуры и поперечные сечения Цели Распознавать многогранники и их части. Визуализировать поперечные сечения пространственных фигур.

Презентация на тему: «11-1 Космические фигуры и сечения. Цели Распознавать многогранники и их части. Визуализировать сечения пространственных фигур». — Стенограмма презентации:

1

2

11-1 Космические фигуры и поперечные сечения Цели Распознавать многогранники и их части Визуализировать сечения пространственных фигур

3

Многогранник — это пространственная фигура или трехмерные фигуры, поверхности которых представляют собой многоугольники.Каждый многоугольник — это грань многогранника. Ребро — это сегмент, образованный пересечением двух граней. Вершина — это точка пересечения трех или более ребер.

4

Вершины: Ребра: Грани:

5

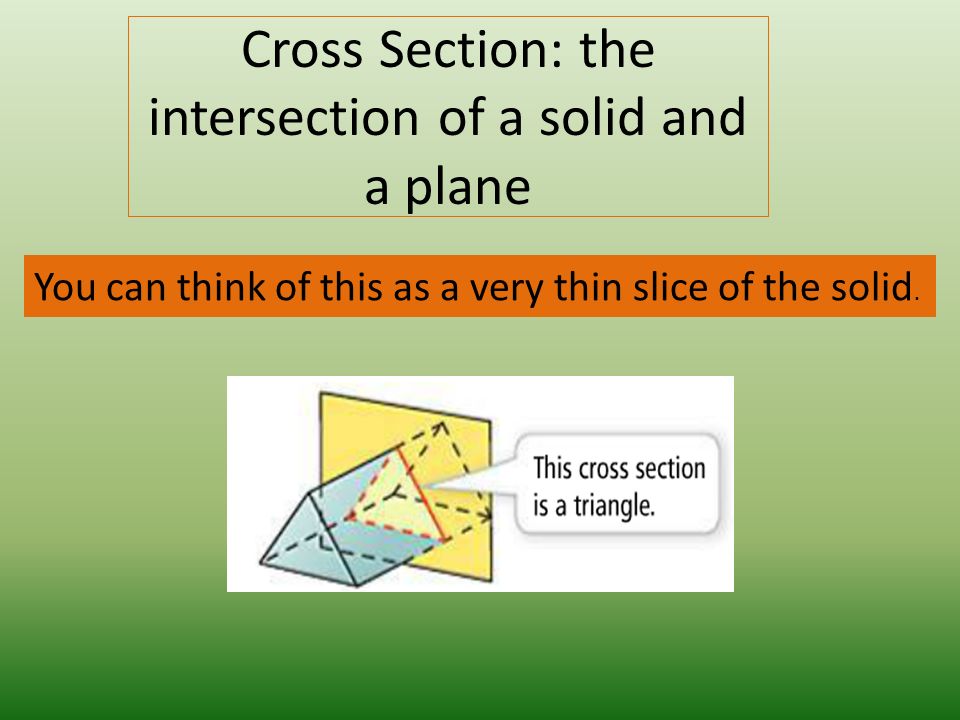
Поперечное сечение: пересечение твердого тела и плоскости. Вы можете думать об этом как об очень тонком срезе твердого тела.

6

Опишите поперечное сечение. Поперечное сечение представляет собой прямоугольник. п. 691: 1, 3, 6-8, 18-20

.