Как из бумаги сделать объемные фигуры: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника ✅ igrad.su
Геометрические фигуры из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Читайте также:
делаем поделку в технике оригами
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков), нужно начать с простых геометрических фигур. Такие изделия подойдут для школьников для хорошего визуального представления разных фигур.
Мастерим куб
Итак, для сегодняшнего мастер-класса нам пригодится бумага, схемы, клей, ножницы, линейки и немножечко терпения.
Куб — самая простая фигура для оригами, простой многогранник, в котором каждая грань является квадратом. Схему для создания развертки можно распечатать на принтере, либо начертить самим. Для этого выбрать размеры граней. Ширина листа бумаги должна быть не менее 3 сторон одного квадрата, а длина не более 5 сторон. Начертить в длину листа четыре квадрата, которые станут боковыми сторонами куба. Рисовать строго на одной линии, вплотную. Над и под одним квадратом нарисовать по одному квадрату. Дорисовать полоски для склеивания, благодаря которым грани будут соединяться между собой. Наш куб уже практически готов!
Далее тонким слоем клея равномерно размазать по местам соединения. Склеить эти поверхности и закрепить на некоторое время с помощью скрепки. Клей будет схватываться около 30-40 минут. Таким образом склеить все грани.
Поделка посложнее
Конус делается немного сложнее. Для начала нарисовать циркулем окружность. Вырезать сектор (часть кружка, ограниченная дугой окружности и двумя радиусами) из этой окружности. Острота конца конуса зависит от вырезанной части большого сектора.
Склеить боковую поверхность конуса. Далее измерить диаметр основания конуса. Циркулем нарисовать окружность на листе бумаги. Затем дорисовать треугольнички для склеивания основы с боковой поверхности. Вырезать. После приклеить основание к боковой поверхности. Поделка готова!
Сложный параллелепипед
Параллелепипед — сложная фигура многогранник, у которого 6 граней и каждая из них параллелограмм.
Чтобы сделать параллелепипед техникой оригами, нужно начертить основание — параллелограмм любого размера. С каждой его стороны нарисовать боковые стороны — тоже параллелограммы. Далее от любой из боковых сторон дорисовать второе основание. Добавить места для склеивания. Параллелепипед может быть прямоугольным, если все стороны имеют прямые углы. Затем вырезать развертку и склеить. Готово!
Пирамида-оригами
Пришло время сделать пирамиду из бумаги. Это многогранник, основание которого — многоугольник, а другие грани — треугольники с общей вершиной.
Для начала нужно выбрать размеры пирамиды и количество граней. Далее нарисовать многогранник — он будет основанием. Смотря на количество граней, это может быть также треугольник, квадрат, пятиугольник.
От одной из сторон нашего многогранника нарисовать треугольник, который будет боковой стороной. Затем нарисовать еще треугольник, чтобы одна его сторона была общей с первым треугольником. Нарисовать их столько, сколько сторон в пирамиде. Далее дорисовать полоски для склеивания в необходимых местах. Вырезать и склеить фигуру. Пирамида готова!
Бумажный цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, которые ее пересекают.
Нарисовать прямоугольник на бумаге, в которой ширина — высота цилиндра, а длина — диаметр. Любители геометрии знают, что отношение длины прямоугольника к диаметру определяется формулой: L=nD, где L — длина прямоугольника, а D — диаметр цилиндра. С помощью этого вычисления узнать длину прямоугольника, которого будем рисовать на бумаге. Дорисовать маленькие треугольнички для склеивания деталей.
Затем нарисовать на бумаге два круга, диаметром как цилиндр. Это будет верхнее и нижнее основания цилиндра. Далее вырезать все детали. Склеить боковую поверхность цилиндра из прямоугольника. Дать детали высохнуть и приклеить к нему нижнее основание. Снова подождать, пока высохнет, и приклеить верхнюю основу. Готово!
Видео по теме статьи
Самые лучшие посты
Объемные фигуры из бумаги своими руками
В наши дни, наверное, из бумаги уже делают все. Огромная востребованность, данного продукта обусловлена широкой известностью и обширной сферой применения. Сегодня мы поговорим про объемные фигуры из бумаги своими руками. Для некоторых людей такое хобби перерастает в прибыльную профессию, ведь про их экспонаты можно только сказать, что это настоящее произведение искусства.
Благодаря основным свойствам бумаги: мягкости, гибкости и хорошему склеиванию, было изобретено множество видов изготовления объемных фигурок.
В какой технике делаются объемные фигуры из бумаги
Наиболее известные техники выполнения фигур из бумаги перечислены ниже.
Квиллинг — техника спиралек


Квиллинг — техника, открытая в 15 веке н.э., по которой вырезаются длинные полоски бумаги шириной от 2 до 10 мм и затем с помощью ножниц или ножа скручиваются в спирали или замысловатые узоры. Приклеивается все это к основе или соединяются составные части между собой. Таким образом делаются игрушки, украшаются вазы и шкатулки, даже делаются целые картины.
Оригами — японский интеллект


Исторически оригами зародилось в качестве искусства складывания бумаги в религиозных целях в высших сословиях древнего Китая. В те времена только что изобретенная бумага была очень дорога и ее могли позволить себе только богатые люди, так что украшения, религиозные символы и другие фигуры из бумаги приобрели большую популярность. Техника складывания фигурок и оберегов из бумаги была доступна лишь избранным. Только в 19 веке оригами попало в Европу и приобрело популярность, в том числе среди детей. Оригами для детей используется в качестве упражнений на развитие мелкой моторики и воображения. В 60-х годах 20 века появилось модульное оригами.
Модульное оригами — больше форм и фантазии


В технике модульного оригами объемные фигуры из бумаги собираются из большого количества одинаковых частей (модулей). Каждый модуль складывается по правилам классического оригами из одного листа бумаги, а затем модули соединяются путём вкладывания их друг в друга. При этом сила трения не даёт конструкции распасться. В технике модульного оригами часто делают коробочки, плоские и объемные звезды, объекты шарообразной формы, которые в России получили не совсем точное название кусудама, так как первоначально кусудама предполагала сшивание модулей в шар.
Мокрое оригами — ближе к реальности


Есть еще один вид популярного оригами — это мокрое складывание. Для придания плавных линий бумага слегка смачивается с помощью губки или пульверизатора. Чаще всего используется для создания фигурок животных. Мокрая бумага более податлива и после высыхания лучше держит форму. Особенностью является то, что намочив конструкцию снова — можно придать ей другую форму, не порвав бумагу.
Киригами — объемы из плоскости


В технике киригами можно использовать ножницы и клей. Поделки в технике киригами чем-то напоминают детские книжки-панорамы. Также эту технику часто сравнивают с ‘pop-up’ — открытками. В отличие от традиционных pop-up-открыток, эти бумажные модели обычно надрезают и складывают из одного листа бумаги. Чаще всего разрабатывают трехмерные воспроизведения архитектуры, геометрические узоры и различные повседневные объекты и др.
Кусудама — округлые формы


Техника кусудама имеет тот же принцип, что и модульное оригами. Главным отличием является то, что фигурки имеют шарообразную форму, а детали для соединения могут быть не только вложены одну в другую, но также склеены или сшиты.
Cubecraft — квадратный колобок с многими лицами


Эта современная техника выполнения поделок из бумаги. В этой технике все фигурки складываются по одной схеме. Смысл в том, что можно делать фигурки различных известных персонажей из кино, комиксов, мультфильмов, а также реальных личностей: политических деятелей, музыкантов, актеров и пр. Такие фигурки ставятся на стол в качестве напоминания или просто порадовать взгляд.
Папье-маше — вспоминаем детство


Название техники папье-маше переводится с французского, как «жеваная бумага». Но вы удивитесь, когда узнаете, что родиной этой техники является Китай. Техника заключается в многослойном наклеивании вымоченных в клейстере кусочков бумаги. Затем фигуры из бумаги грунтуются и раскрашиваются. Из папье-маше можно сделать все, что угодно (вазочки, игрушки, кружки), но чаще всего делают маски.
Декупаж — украсить старые вещи


Декупаж в переводе означает «вырезание». Чаще всего техника декупаж используется для старой мебели — вырезаются какие-нибудь драконы или птицы, растения или животные. Это придает новый блеск старым вещам. Используется также при создании эксклюзивных предметов интерьера, при оформлении одежды и изготовлении модных аксессуаров.
Торцевание — квиллинг по-новому


В технике торцевания получается изготовить красивые открытки или даже картины. В квиллинге используются длинные полоски, которые накручиваются на тонкую палочку. Здесь же нарезаются небольшие квадраты. Затем, к центру квадрата прикладывается палочка, и на нее накручивается этот квадратик. Получившаяся деталь наклеивается на основу. Получается иногда необычно и весьма объемно.
Пейп-арт — имитация металла


Эта техника придумана в 2006 году и в своей основе содержит имитацию металла и дерева из бумажных салфеток. Техника имитирует резьбу по дереву или чеканку из металла. Окраска и патинирование придает натуральность текстурам. Смоченные в воде полоски из салфеток скручиваются в нитки, затем из них выкладывается узор и закрепляют клеем. После высыхания остается только покрасить и придать естественность.
Айрис фолдинг — «радужное складывание»


Чтобы сделать поделку в этой технике, нужно нарезать несколько полосок бумаги разного цвета и уложить их по спирали или другим причудливым способом. Выглядит все это как многогранная фигура. Наложение полупрозрачных бумаг друг на друга дает интересные эффекты при декорировании.
Пергамано — кропотливый труд


Узоры и украшения в этой технике выполняются на кальке или пергаментной бумаге с помощью перфорирования и тиснения. Чаще всего техника пергамано используется в изготовлении открыток и приглашений.
Катагами — нужен острый нож


Еще немного Японского бумажного искусства. Катагами — искусство вырезания целых картин из рисовой бумаги с помощью специального острого ножа и трафарета или по нарисованной линии. Чаще всего используется для картин.


Коллаж — старые журналы — в бой!


Коллаж — это изображение, составленное из различных бумажных кусочков (обоев, газет, журналов, фотографий и пр.), отличающихся по цвету и фактуре. Раньше вырезали картинки из журналов, газет, книг и украшали ими вещи (вспомните бабушкин чемодан или трюмо). Сейчас эта старинная техника вновь стала модной и широко распространена в различных странах при декорировании сумочек, шляпок, подносов, ёлочных украшений, солнечных часов, шкатулок, посуды, упаковок и т. д.
Бумажное моделирование — бумага превращается…


Особого интереса, заслуживает бумажное моделирование. Вы можете создать практически любую объемную фигуру из бумаги своими руками. Начиная от военной техники, памятников архитектуры и заканчивая различными видами животных, как известных всем, так и вымышленных. Конечно, в идеале нужно уметь делать все (чертежи, детали и прочее) своими руками, но для начала можно воспользоваться интернетом. Через поиск Вы сможете отыскать массу чертежей и макетов, которые можно распечатать на принтере, вырезать и склеить. Есть даже специальные сайты, которые хранят чертежи бумажных моделек: самолетов, автомобилей, героев фильмов и мультфильмов.


Все перечисленные техники поделок из бумаги имеют свои нюансы, преимущества и недостатки. Но самое главное, при выборе каким видом бумажного искусства заняться, я советую руководствоваться исключительно собственным сердцем. Для того, чтобы сделать завораживающую фигурку, надо по-настоящему любить это дело.
Это кропотливая работа, которая требует внимательности и терпения, и только при сильном желании можно все сделать, так как надо. Наградой для Вас, могут стать восхищенные взоры друзей и похвалы в Ваш адрес.
Бумажные изделия смотрятся очень красиво, если все ровненько вырезать и собрать. Главное, что для создания таких фигур не требуется специальных навыков. Достаточно внимательно все соединить. Немного попрактиковавшись, у Вас станет все получаться значительно быстрее и ровнее.
Пример, насколько необычными могут быть фигуры из бумаги, можно увидеть из нижеприведенного видео. Советую всем посмотреть, ведь это действительно необычно и шедеврально.
Геометрические фигуры из бумаги покоряют четкостью, даже строгостью своих линий, при этом выглядят очень оригинально, а сделать их весьма просто. Имея лист бумаги, клей-карандаш и несколько свободных минут, можно создать своими руками удивительный декор для дома.
![]()
Можно превратить их в елочные игрушки или подвесы к люстре:
![]()
![]()
Коробочки для подарков:
![]()
Или «печенье» с пожеланиями, предсказаниями, поздравлениями:
![]()
Можно стильно украсить ими стены:
![]()
Или создать необычный арт-объект:
![]()
«Цветочную» композицию:
![]()
К вечеринке можно сделать макси-украшения для интерьера:
![]()
И мини — в качестве шуточных подарков гостям:
![]()
Распечатки вырезаются по сплошным линиям и складываются по пунктирным, затем промазываются клеем по выступающим клапанам и собираются в красивые объекты, использовать которые, как мы уже увидели, можно совершенно по-разному.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
А еще я хочу поделиться с вами бумажной моделью настоящего глобуса. Такую вещь будет интересно делать с детьми, она больше напоминает бумажный конструктор и для ее сборки не требуется клей.
Пошаговая сборка:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Распечатки с выдержанным масштабом. Вам понадобится по одному экземпляру листов 1-6 и восемь экземпляров листа 7. Распечатки лучше делать на бумаге с максимальной плотностью, доступной вашему принтеру, или же наклеить тонкую бумагу на картон или кардсток:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вдохновляйтесь и украшайте свой дом необычными объектами. Приятного творчеста!
Спасибо за внимание.
![]()

Лучший способ показать малышу окружающий мир — дать почувствовать его на ощупь, ведь маленькую кроху хлебом не корми — дай дотронуться до заинтересовавших ее предметов, тем более, если это разноцветные геометрические тела оригами, сделанные своими руками.
60
298 т.
Яркие
объемные поделки из бумаги привлекут
внимание ребенка и уж точно не дадут
скучать. А Вы незаметно и с задором
проведете горячо любимое чадо в мир
занимательной
геометрии.

Не
знаю, как Вам, дорогие читатели, а мне
эти красочные оригами напомнили
драгоценные
камни
.
Так почему бы о каждом из них не рассказать
малышу что-нибудь интересное, сравнивая
очередное геометрическое тело с рубином,
сапфиром, турмалином и так далее?
А
пока на цветных листах распечатайте
схемы
поделок
и, сделав необходимые изгибы, и склейте
в нужных местах. Уверен, у Вас все
получится!
Тетраэдр
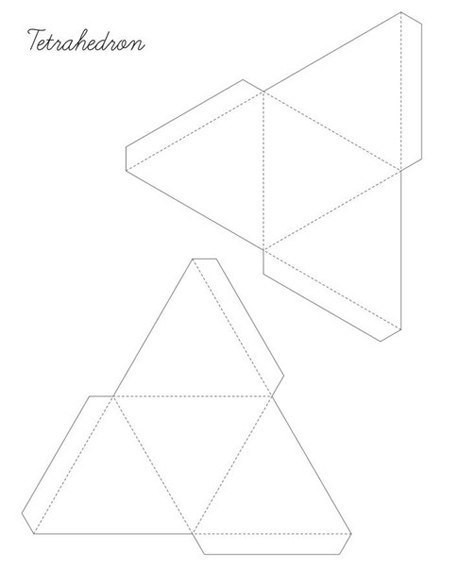
Октаэдр
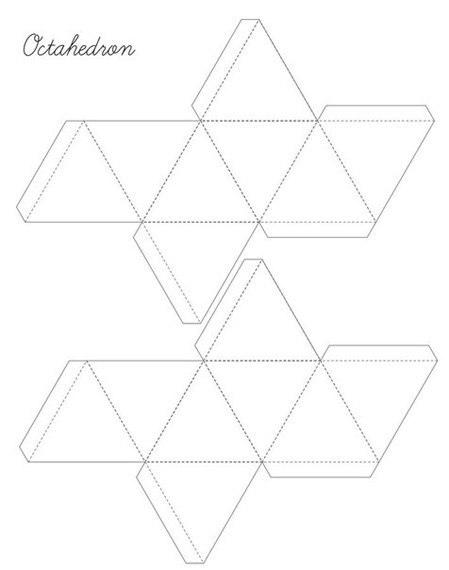
Икосаэдр
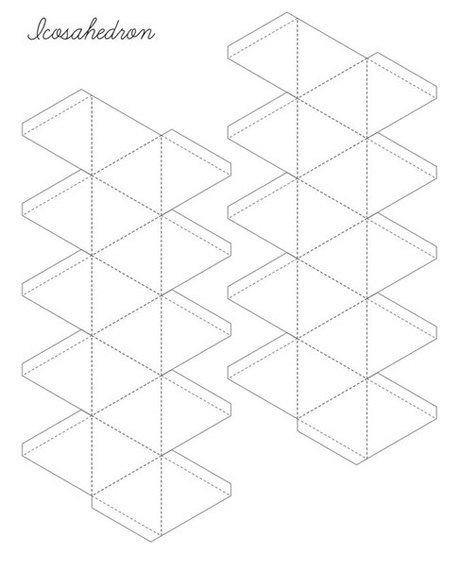
Додекаэдр
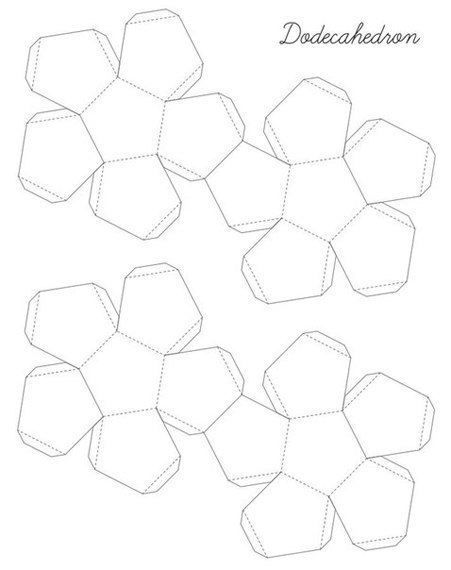
Куб

У Вас должны получиться
вот такие заготовки:

А это уже готовые
камешки-многогранники. Дерзайте!

Веселых игр, занимательных
историй и всестороннего развития Вашему
малышу!
Заметили орфографическую ошибку? Выделите её мышкой и нажмите Ctrl+Enter
Каждый начинающий моделист, будь то взрослый или ребёнок, должен изучить и запомнить основы работы с бумагой. От этих элементарных знаний зависит качество создаваемых полигональных фигур и скульптур. Всем следующим приёмам нужно учить детей с малого возраста, чтобы в повседневном упражнении они уже делали это не задумываясь, а в результате модели будут получаться с легкостью. Я попробую раскрыть особенности и тонкости обучения, проектирования и создания разверток для трёхмерных фигур, а также сборки и склеивания низкополигональных моделей.

low poly викинг
Существуют три разновидности, но наша задача найти отличия. High poly или высокополигональное моделирование, подразумевает создание объекта с большим числом полигонов( эффект сглаживания),или если сказать по другому—точной его копии. low poly, в переводе низкополигональное моделирование, используется для создания фигуры с небольшим числом полигонов, что придает некий лофт(грубость) модели. Обычно, для экономии ресурсов, когда не требуется высокая детализация, а так же для создания иллюстраций, которые набирают большую популярность в последнее время.
Полигональное моделирование из бумаги
Позволяет визуализировать объект с помощью специальной сетки. Оно появилось в то время, когда для определения местонахождения точки необходимо было вручную вводить её координаты по осям X, Y, Z. Если три точки координат задать как вершины и соединить их ребрами, то получится треугольник, который в 3d моделировании называют полигоном. Как правило, он имеет свою текстуру и цвет, а если объединять несколько,то получится модель. Вместе, они составляют сетку или объект.

modeling decor
Для того, чтобы края модели не имели граненого вида, необходимо, чтобы они были малого размера, а поверхность состояла из маленьких плоскостей. Если предполагается точное моделирование, либо в дальнейшем увеличение его изображения, то необходимо строить модель с большим количеством граней, хотя, если на модель смотреть издали без приближения, достаточно будет небольшого количества. Это и есть полигональное моделирование. Сетка состоит из под объектов и может состоять из огромного количества одинаковых ячеек:
вершина – точка соединения рёбер, может быть множество рёбра – границы граней грани – ячейки сетки, участки плоскости. Чаще всего треугольной или четырехугольной форму.
Что бы создать 3D модель необходимо работать (с частями) подобъектами. Объединяем и делим, меняем их форму и размер, вращаем, а также применять другие операции, которые позволяются в специализированном программном обеспечении.
Набор программ для создания и 3D-развертки
Естественно, чтобы получить желаемую фигуру пригодятся специальные программы. Я расскажу о самых актуальных и незамысловатых. Они могут помочь превратить некоторые идеи в красивые творения и прототипы, которые можно использовать в самых разных дизайнерских ноу хау. Эти редакторы доступны для изучения, освоить их сумеют даже новички за короткий промежуток времени. Использование ПО позволило на огромную ступень повысить уровень кинематографа компьютерных игр, дизайна интерьера, архитектурных и скульптурных решений. Выбор оптимального программного обеспечения часто бывает трудным, так как непросто найти подобрать всё в одном, что бы весь необходимый функционал был в одном месте.
Совокупность граней, из которых будет состоять оболочка изделия, являются сеткой. Изготовление несложное, поскольку они имеют четко определяемые внешнюю и внутреннюю область, и поэтому дополнительных параметров и вычислений не понадобится. Но этот способ требует терпения и усидчивости, потому что необходима сосредоточенность, активная мозговая деятельность и тысячи кликов мышкой. Будьте внимательны, даже маленькие погрешности способны испортить процесс.
Pepakura Designer
Умеет работать со множеством форматов 3D моделей, например 3DS, DXF, MQO, LWO. Список можно просмотреть на официальной странице программы, думаю это сделать не сложно.
Обратите внимание: программа не имеет возможности создавать сами трехмерные макеты, как выше указанные в списке. Также нет никакого редактора, но зато разработчики предлагают нам переводить их в 2D форматы, после вы можете распечатать схему на принтере и потом создать настоящее чудо.
Как правило такой набор или развертку бородатого воина вы не скачаете в бесплатном доступе. Есть множество профессиональных распечаток, но их можно только приобрести за символическую плату к примеру на площадке Etsy.

Папекура Дизайнер создаёт и редактирует 3D заготовки. Чертеж-выкройку развернутую, которую затем можно вывести на печать в нужном масштабе, вырезать и склеить. Конечно, такой подход подразумевает изрядную работу, но выбирать не приходится — более дешёвого и доступного метода “материализации виртуальных объектов” еще не придумано. Pepakura Designer поддерживает различные форматы 3D моделей созданных в программах 3Dstudio, Lightwave, AutoCad и др. Программа создает развертку 3-х мерного изображения для последующей печати на принтере. Она выдаст рисунок с готовыми местами для склеивания и вырезания.
Pepakura Viewer
Менее мощный инструмент может только просматривать работы, не имея возможности изменять их. Помимо этой прямой функции, вы можете увеличивать, уменьшать, крутить, вертеть, выставлять углы и делать прочие безобидные махинации. Это всё, что потребуется для успешной склейки.
Делаем модели из бумаги, пепакура для развёртки
На примере кота мы видим, как выглядят схемы и развёртки полигональных фигур. Это также может быть собака, мышка, или другое животное. Для того что бы всё получилось нужен хороший качественный набор в pdf. Как правило бесплатные имеют дефекты, так как создавались новичками, профи уже требуют цену за свой труд.

Натуральный кот и шикарный олень из бумаги. Скульптура в мини-размере для украшения интерьера.

Дизайнерский loft черно-золотой бык в декоре стены. Если вы создаёте крупные фигуры розового слона или большую голову лося вам нужен плотный картон для моделирования.



model head
Черно-белый набор смешных человечков из картона и сложная модель Хаски.


Полигональная фигура их методы и способы построения
Создаются тремя основными методами, которые используют в объединённом варианте и по отдельности. Использование примитивов—за основание берут готовые геометрические фигуры вроде куба или цилиндра. Конструируем нужную модель путем вытягивания подобъектов и деления существующих граней. Также вытягиванием новых граней из полигона-исходника , когда каждый следующий появляется из предыдущего.
Предусмотрено три основных способа построения визуализации.
- Для придания нужной формы меняется положение рёбер, их размеры.
- Проводятся манипуляции с вершинами, их перемещение, удаление и т.д.
- Грани-полигоны используются для более сложных действий. Это придание формам выпуклости или наоборот заостренности. Возможно сглаживание или вдавливание поверхности—работаем с плоскостями.
Необходимый набор для сборки, схемы и развертки полигональной фигуры
Позаботьтесь о хорошем, удобном столе и стуле, нужно, что освещение падало из-за левого плеча, используйте настольную лампу. Чтобы не выпачкать стол клеем застелите его плёнкой или положите лист стекла с зашлифованными краями, чтобы не порезаться. Чтобы научиться складывать базовые изделия, вам понадобятся простые приспособления вроде ножниц, канцелярского ножа, клея ПВА и кисточки для его нанесения.

Отдайте предпочтение строительному клею ПВА — из всех разновидностей у него наиболее густая консистенция, он не портит бумагу, делая её мокрой и вязкой, как обычный. Используются разные виды — от папиросной до обычного картона. Новичкам советуют начинать с акварельной, в 200 грамм на м2 для крупных элементов и чертёжной разновидности 140-160 грамм – при разработке мелких частей.
Бумага для паперкрафта и клей для бумажных моделей
Основным материалом для создания является, естественно, обычная бумага, но так как она не сильно надёжная и хрупкая, советуем обратить внимание на полукартон, либо же обыкновенный картон. Детали из него более крепкие и придают готовому творению износостойкость.

Удивительный кит с подсветкой—эксклюзивный ночник в спальне вашего ребёнка
У каждого мастера имеются свои секреты, вот и мы хотим поделиться с вами открытием.
Заготовки гораздо удобнее приклеивать узким двухсторонним скотчем. Он скрепляет моментально и угрозы “расклеиться” ваше творчество не потерпит.
Но также неплохой связующий предмет для элементов – клеевой раствор. Выбирайте вариант, который удобнее.
Модель из бумаги
Рабочий процесс создания проходит в несколько простых этапов. Перед началом процесса мастер определяется, какую фигурку он хочет сконструировать. На самом деле, можно смастерить практически любое изделие, но бумажное моделирование чаще предполагает такие варианты:
- многогранники с выпуклыми и вогнутыми углами, геометрические фигуры
- копии зданий в масштабе
- макеты автомобилей премиум класса
- танки, тяжелые орудия, бронемашины
- поезда, корабли и подлодки, самолеты

Бумага для моделирования—основной рабочий материал. Следует уделить особое внимание её качеству! Для начального творчества лучше всего использовать обыкновенные листы формата А4, они имеют хорошее качество и является самой белоснежной по отношению к другим маркам. Плотность – 80 г/м. Советую приобретать специальную, для черчения.
Создание макета
Многие укрепляют эпоксидкой или красят краской. Я не рекомендую, потому что лучше взять качественную бумагу и собрать аккуратно, чем некачественно нанести краску из-за чего сгладятся грани, что придаёт грубости. К тому же модели не требуют особой прочности, так как приспособлены для украшения стен. Они собираются из предварительно вырезанных и согнутых деталей. Развертки необходимо распечатывать на бумаге 170—200 г/м². Это сделает её устойчивой.

группа заготовок на рабочем столе
При вырезании каждой детали обязательно нумеровать каждую. Для сгибов используйте линейку. Чтобы придать детали округлость, оберните её вокруг карандаша. От силы скручивания зависит сама форма. Тот же способ используйте для кривых поверхностей.
Сборка: особенности процесса
Необходимые материалы:
- иголка для нанесения клея в труднодоступных местах
- papercraft развёртки
- кисточка
- острые ножницы или канцелярский нож
- металлическая линейка
- любая ровная поверхность
- клей (не используйте ПВА, после высыхания он деформирует изделие), но на собственном опыте убедились, что эффективнее использовать двухсторонний скотч, шириной 2 мм, в этом случае обязательно наличие пинцета
- дотс для продавливания сгибов
Для жёсткости деталь по сгибам и пустоты внутри заполняем монтажной пеной, но без фанатизма, чтобы она при расширении не деформировала внешний вид.
Видео-урок “Низкополигональные модели”

Арт-голова оленя станет чудесной маской на маскарад, либо вечеринку.

Сказочный декор для фотостудии.




Полигональная модель и основные рекомендации
Предпочтение отдаем геометрическим фигурам из четырехугольников. Проще в деформации, что позволит сэкономить время,не проводя ненужных манипуляций. Треугольники применяем как можно меньше. Также не стоит использовать сложные геометрические фигуры, с большим количеством ребер и углов, это может привести к деформации текстуры.
Советуем визуализировать только необходимые элементы, построение дополнительных конструкций усложняет, если это мелкие детали, их можно делать, используя текстуры. Эта техника рассчитана на создание объектов с точными формами и чёткими контурами. Маленькие грани строят целостное, они имеют цвет и форму. Указанный способ котируется в промышленном дизайне.


Полигональные изделия из металла или пластика
Множество интересных идей можно воплотить из такого “сурового” материала, как металл или пластмассы. Такие изделия – арт-объекты, они станут великолепным украшением фотозоны, ресторана, дачного участка, коттеджного посёлка, либо парка. Внешний вид фигур ограничен только бюджетом и фантазией заказчика.
Уличный пёс-сторож.


Полигональная пантера с эфектом сглаживания.

Лошадь из стеклопластика.

Ben Foster Sculpture
Полигональные фигуры в интерьере и креативные дизайнерские идеи
Практически всеми возможными фигурами можно украшать детскую спальню, офис, спальню, кухню. От вашей фантазии зависит масштаб конструкции, стоит начать с небольших фигур что бы потренитроватся и понять какие недостатки вылезут и после этого приступать к моделям с человеческий рост и выше.

loft papercraft для дома

полигональная фигура в интерьере


лисенок и цветы

голова фламинго
Настенная скульптура – бык.

Заяц – отличное дополнение к пасхальной корзинке.



Низкополигональные миры
Наверное, все уже слышали о подобного рода иллюстрациях. В процессе создания объёмного 3D-изделия, она формируется при помощи полигонов. Чем их численность выше, тем реалистичнее будет вид. Раньше всегда ценилась высокая степень проработки изображений и мастера стремились к высокому числу полигонов, заготовки с низким числом были лишь набросками, считались незаконченной работой.
Mat Szulik—удивительный художник и необычайной красоты миры


французская улица, кофейня и дама в шляпе
Christripes

Vitaliy Prusakov

Kirill Kodochigov

Jona Dinges

Для сборки сурового викинга с топором потребуется неделя усидчивости, не меньше.


Paul DOUARD




Gareth David

Jeremiah Shaw
Пример того как можно сочетая два цвета (серый и зелёный) и три простые фигуры дерево, трава и камень создать низкополигональный шедевр, причем масштаб зависит только от вашего воображения и возможностей.
Видео мастер класс создание развертки полигональных фигур
Геометрические фигуры | Планета Оригами
Простая оригами ёлка-новогодняя игрушкаВидео уроки
0
Наряду со сложными моделями оригами, на сборку которых порой может уйти целый день, хотим предложить вам сборку достаточно простой, но очень симпатичной ёлки.
Куб в наушниках по схеме Джереми Шейфера (Jeremy Shafer)Видео уроки
0
Джереми Шейфер (Jeremy Shafer) — известный мастер оригами, который славится своими необычными моделями, состоящими из многочисленных деталей, но
Простой держатель для карт — сюрикенВидео уроки
0
Бумажные оригами модели могут представлять собой не только симпатичных животных и птиц, но и совершенно обыденные вещи, которые имеют практическое значение.
Вращающийся тетраэдр по схеме Tomoko FuseВидео уроки
0
Сегодня мы предлагаем вашему вниманию очень интересную модель в технике подвижного оригами. Это замечательная бумажная игрушка-тетраэдр от мастера оригами Tomoko Fuse.
Простая шутиха из бумаги: оригами для детейВидео уроки
0
Как часто вы устраиваете вечеринки? А как часто вам приходится придумывать различные декорации и антураж, чтобы создать соответствующую обстановку?
Тесселяция «Кельтский круг» по схеме Robin ScholzВидео уроки
0
Фото by Paula Otero Сегодня на нашем сайте очень интересная и трудоемкая в сборке модель от мастера оригами по имени Robin Scholz. Представляем вашему
Burr Puzzle по схеме Barlaham Benítez Vargas (Froy)Видео уроки
0
Фото Mir Numan Сборка различных геометрических фигур занимает особую нишу в технике оригами. Сегодня мы предлагаем вам сложить так называемый Burr Puzzle
Шестиконечная звезда по схеме Stephan WeberВидео уроки
0
Складывать различные оригами звезды можно несколькими способами. Первый из них — из модулей, но не из обычных треугольных для объемных моделей, а
Оригами солнце от MélisandeГеометрические фигуры
0
Фото by Mélisande* Сборка различных оригами животных, птиц и других моделей живых существ, несомненно, интересна. Однако в мире оригами существуют и другие
Подарочная коробочка с гортензией от Dasa Severova и Shuzo FujimotoВидео уроки
0
Фото by happyfolding.com Одной из самых интересных и сложных разновидностей оригами складывания смело можно назвать тесселяции. Эти многоуровневые цветы и «
Коробочка-лотос и рамка для фотографий от Джереми ШейфераВидео уроки
0
Джереми Шейфер, насколько вы уже успели заметить, не из тех мастеров оригами, которые довольствуются простыми плоскими поделками. Все его модели —
Гибкая пирамида-трансформер от Джереми Шейфера (Jeremy Shafer)Видео уроки
0
Соскучились по весельчаку Джереми Шейферу? Тогда мы идем к вам! Сегодня в эфире новая поделка этого замечательного мастера, которую он назвал Multiple
Пипетки
Пипетки
используются для очень точного измерения фиксированных объемов жидкости. Наиболее распространенными размерами являются 25 см 3 и 10 см 3 . Хотя пипетки бывают других размеров, вы вряд ли встретите более крупную в лаборатории уровня A, хотя иногда вы можете использовать меньшую, например, 5 см 3 . Маленькие градуированные пипетки также доступны — скорее как капельница с маркировкой на.
Правильное использование пипетки подробно описано в видеосвязи внизу страницы.
бюретки
Бюретки
используются для очень точного измерения переменного объема жидкости — в том числе, конечно, при титровании. Наиболее распространенный размер в лаборатории уровня А — 50 см. 3 .
Если вам нужно отмерить какой-то больший объем жидкости, нет никаких причин, почему вы не могли бы сделать это, наполнив бюретку. Например, был вопрос CIE, в котором вас спрашивали, как бы вы добавили ровно 100 см 3 одного решения к другому.В отчете эксперта предлагается использовать бюретку, добавив две отдельные партии по 50 см 3 . Но если вы собираетесь это сделать, будьте аккуратны — скажите, что вы собираетесь использовать бюретку размером 3 00010 9504 (50 см) дважды .
Опять же, использование бюретки подробно описано в видео ниже.
Измерительные цилиндры
Измерительные цилиндры недостаточно точны , если вам нужно добавить точный объем, и вы не получите оценку, если предложите использовать тот, где бюретка или пипетка будет более подходящей.
В процессе титрования простой пример использования измерительного цилиндра — это то, где вам нужно добавить избыток разбавленной серной кислоты во время титрования манганата калия (VII). Например, вам может быть предложено добавить 10 см 3 разбавленной серной кислоты в жидкость в колбе перед тем, как вы попадете в раствор марганата калия (VII) из бюретки.
Измерительный цилиндр подходит для этого, потому что все, что имеет значение, это то, что кислота в избытке. Пока это правда, точное количество добавленной кислоты не имеет значения.
Полезные видео, показывающие объемные методы
На YouTube много похожих видео, и после того, как вы посмотрите те, что ниже, вам, вероятно, будут предложены и другие. Вы найдете небольшие различия между некоторыми из них. Не позволяйте этому беспокоиться — те, кто ниже, показывают хорошую технику.
Создание точных решений
Приготовление стандартного раствора карбоната натрия
(Размахивание бюреткой, как показано во вводных заголовках, — это , а не , — хорошая техника, но все остальное!)
Другие видео показывают небольшие различия в способах взвешивания карбоната натрия.В этом видео он взвешивается на стакане с часами, а затем все вымывается в стакан. Другой возможностью является взвешивание в бутылке для взвешивания.
Вы также можете просто наклонить карбонат натрия в стакан, не пытаясь перенести все это. Вы можете взвесить контейнер (стеклянный час или бутылку для взвешивания) с тем, что в нем осталось, а затем определить, сколько было добавлено.
Видео, которое я использовал, кажется мне наиболее простым для понимания.
Использование пипетки
Как использовать пипетку
Это отличное видео описание способа использования пипетки для точной работы.Здесь упоминается термин «аликвота», который используется в этом смысле для обозначения измеренного образца, взятого из жидкости.
Использование бюретки и простое титрование
Как использовать бюретку и сделать простое титрование
Отличное видео описание, показывающее, как сделать это очень точно при простом кислотно-щелочном титровании с использованием фенолфталеина в качестве индикатора, при котором щелочь («титрант») превращается в кислоту («аналит»). Не беспокойтесь слишком сильно об этих, возможно, незнакомых терминах.Я не помню, чтобы когда-либо сталкивался с ними на уровне А.
,
круг. Техника объемного прибора
Аппликации из цветной бумаги — традиционный взгляд творчества для детей. Этот вид рукоделия помогает им научиться пользоваться ножницами, развивает мелкую моторику, помогает детям привыкнуть к письму, приучает ребенка быть более осторожным. Каждый ребенок может выполнять нечетную работу, если вы поставите перед ним задачу, которую он может выполнить. Самым простым рисунком для подачи заявки из цветной бумаги является круг. Такое занятие научит детей различать формы и цвета, развивать их воображение и логику.Примерно с 3-х лет в течение 4 лет ребенок уже способен самостоятельно комбинировать необходимые детали и собирать их в определенный состав. Он сможет дать готовую работу родителям и бабушке с дедушкой, получив заслуженную похвалу.
Техника объемного аппликации
Популярный шаблон аппликации из цветной бумаги с круглой формой — божья коровка. Чтобы создать рисунок в объемном методе, достаточно вырезать два красных кружка одинакового размера, один черный полукруг для головы и несколько маленьких кружков для точек на спине насекомого.Глаза божьей коровки можно сделать из специальных наклеек или приклеить заготовку из белой и черной бумаги. Далее один из красных кружков помещается над головной частью, а второй изгибается посередине и приклеивается к первому. Осталось только дополнить фигуру точками на спине, лапах, глазах и усиках.
Животные из цветной бумаги
Методика применения позволяет создавать и разных животных. Итак, из кругов разных диаметров можно сделать осла.Для его изготовления нужен один большой круг и три меньших — для туловища, шеи и ушей. Еще нужно сделать пять маленьких кружков другого цвета для головы и ног и один, совсем маленький, для морды. Оттенки цветной бумаги подбираются на ваш вкус. Например, тело может быть синим, а ноги — красными. Осел сделать немного сложнее, чем божья коровка, потому что иногда ребенку нужно будет рассказать, как добавить детали, если он не справляется.
Ствол осла состоит из круга, не сложенного пополам, но с небольшим углублением, так что остается только живот животного.Ноги состоят из четырех кругов, согнутых пополам. Шея, уши, морда — все это круги, сложенные посередине. Голова — это круг, стороны которого согнуты к центру. После окончания работы к маркеру необходимо будет прикрепить гриву и хвост.
Аппликация из кусочков бумаги
Еще один способ создания аппликации из цветной бумаги с кружочками — заполнить готовый контур теми же заготовками. Таким способом Вы можете сделать змею, ящерицу, рыбу и других животных, которые покрыты чешуей.Но сначала нужно создать трафарет или узор, внутреннюю часть которого нужно будет наклеить кусочками цветной бумаги в виде круга. Независимо от того, какой цвет материала использовать, если вы комбинируете цвета, готовая работа будет гораздо интереснее, и ребенок узнает больше и выберет гармоничные и контрастные оттенки между ними. Этот важный навык поможет ребенку в будущем развивать другие виды творчества. Не обязательно использовать только круглые шаблоны для приложений. Учитесь у детей разным формам и старайтесь сочетать их на картинке.
Модульная аппликация из кружков
В качестве летнего ремесла, которое родители будут делать вместе с ребенком, Вы можете сделать аппликацию из цветной бумаги с кружочками в виде тарелки с ягодами, например, с клубникой. Для этого сначала нужно нарезать два больших круга для тарелки, а затем начать делать ягоды в модульной технике. Перед началом работы желательно подготовить шаблоны для вырезания заготовок и нескольких листов бумаги красного и зеленого цвета. Для одной клубники понадобятся три маленьких зеленых кружочка, из которых будут сделаны листья, и один большой, для самой ягоды.Если вы хотите сделать и уйти за куст, вы можете взять еще три больших зеленых круга, равных по диаметру красным. Затем основание клубники сгибается с обеих сторон, образуя форму, похожую на стакан.
Маленькие зеленые кружочки сложены пополам и склеены близко друг к другу в верхней части ягоды. Черенки для листвы можно нарисовать фломастером, а на их концах разместить три больших круга зеленого цвета, сложенных пополам. Только одна сторона кругов приклеена к основанию. Таким образом, в технике нанесения цвета можно приготовить различные фрукты и овощи и наполнить их тарелкой.
Занятия с цветной бумагой способны пробуждать творческие способности не только у детей, но и у родителей. Техника аппликации используется в различных видах рукоделия, помогает развить точность и умение довести дело до конца.
р >>
,
Другим примером многоканальных данных являются слои в сверточной нейронной сети. Уровень сверточной сети обычно состоит из нескольких каналов (обычно сотен каналов). Каждый канал описывает различные аспекты предыдущего уровня. Как мы осуществляем переход между слоями с разной глубиной? Как преобразовать слой с глубиной n в следующий слой с глубиной м ?
Прежде чем описывать процесс, мы хотели бы уточнить некоторые термины: слои, каналы, карты функций, фильтры и ядра.С иерархической точки зрения понятия слоев и фильтров находятся на одном уровне, а каналы и ядра находятся на одном уровне ниже. Каналы и карты функций — это одно и то же. Слой может иметь несколько каналов (или карт объектов): входной слой имеет 3 канала, если входные данные являются изображениями RGB. «Канал» обычно используется для описания структуры «слоя». Точно так же «ядро» используется для описания структуры «фильтра».
Разница между «слоем» («фильтром») и «каналом» («ядром»).
Разница между фильтром и ядром немного хитрая. Иногда они используются взаимозаменяемо, что может создать путаницу. По сути, эти два термина имеют тонкую разницу. «Ядро» относится к двумерному массиву весов. Термин «фильтр» предназначен для трехмерных структур из нескольких ядер, собранных вместе. Для 2D-фильтра фильтр такой же, как и для ядра. Но для 3D-фильтра и большинства сверток в глубоком обучении — это набор ядер. Каждое ядро уникально, подчеркивая различные аспекты входного канала .
С этими концепциями многоканальная свертка происходит следующим образом. Каждое ядро применяется к входному каналу предыдущего слоя для генерации одного выходного канала. Это процесс ядра. Мы повторяем такой процесс для всех ядер, чтобы сгенерировать несколько каналов. Каждый из этих каналов затем суммируется, чтобы сформировать один выходной канал. Следующая иллюстрация должна сделать процесс более понятным.
Здесь входной слой представляет собой матрицу 5 x 5 x 3 с 3 каналами.Фильтр представляет собой матрицу 3 x 3 x 3. Во-первых, каждое из ядер в фильтре применяется к трем каналам входного слоя отдельно. Выполняются три свертки, в результате чего получаются 3 канала размером 3 x 3.
Первый шаг двумерной свертки для многоканальных каналов: каждое из ядер в фильтре применяется к трем каналам входного слоя отдельно. Изображение взято из этой ссылки.
Затем эти три канала суммируются вместе (поэлементное сложение), чтобы сформировать один отдельный канал (3 x 3 x 1).Этот канал является результатом свертки входного слоя (матрица 5 x 5 x 3) с использованием фильтра (матрица 3 x 3 x 3).
Второй этап двумерной свертки для многоканальных каналов: затем эти три канала суммируются вместе (поэлементное сложение) для формирования одного единственного канала. Изображение взято из этой ссылки.
Эквивалентно, мы можем думать об этом процессе как о перемещении матрицы 3D-фильтра через входной слой. Обратите внимание, что входной слой и фильтр имеют одинаковую глубину (номер канала = номер ядра). 3D-фильтр перемещается только в двух направлениях, по высоте и ширине изображения (поэтому такая операция называется 2D-сверткой, хотя 3D-фильтр используется для обработки объемных данных 3D). В каждой скользящей позиции мы выполняем поэлементное умножение и сложение, что приводит к единственному числу. В примере, показанном ниже, скольжение выполняется в 5 положениях по горизонтали и 5 положениях по вертикали. В целом, мы получаем один выходной канал.
Еще один способ думать о двумерной свертке: думать о процессе, как о перемещении матрицы 3D-фильтра через входной слой.Обратите внимание, что входной слой и фильтр имеют одинаковую глубину (номер канала = номер ядра). 3D-фильтр перемещается только в двух направлениях, по высоте и ширине изображения (поэтому такая операция называется 2D-сверткой, хотя 3D-фильтр используется для обработки объемных данных 3D). На выходе получается однослойная матрица.
Теперь мы можем видеть, как можно делать переходы между слоями с разной глубиной. Допустим, входной слой имеет Din каналов, и мы хотим, чтобы выходной слой имел Dout каналов.Нам нужно просто применить фильтры Dout к входному слою. Каждый фильтр имеет ядра Din . Каждый фильтр обеспечивает один выходной канал. После применения фильтров Dout у нас есть каналов Dout , которые затем могут быть сгруппированы для формирования выходного слоя.
Стандартная 2D свертка. Отображение одного слоя с глубиной Din на другой слой с глубиной Dout с помощью фильтров Dout .
На последнем рисунке предыдущего раздела мы видим, что мы фактически выполняли свертку для трехмерного тома.Но, как правило, мы по-прежнему называем эту операцию двумерной сверткой в Deep Learning. Это двумерная свертка на трехмерных объемных данных. Глубина фильтра равна глубине входного слоя. 3D-фильтр перемещается только в 2-х направлениях (высота и ширина изображения). Результатом такой операции является 2D-изображение (только с 1 каналом).
Естественно, есть 3D свертки. Они являются обобщением двумерной свертки. Здесь в трехмерной свертке глубина фильтра меньше глубины входного слоя (размер ядра <размер канала).В результате 3D-фильтр может двигаться во всех 3-х направлениях (высота, ширина, канал изображения) . В каждой позиции поэлементное умножение и сложение дают одно число. Поскольку фильтр скользит по трехмерному пространству, выходные числа также располагаются в трехмерном пространстве. В результате получается 3D-данные.
В свертке 3D, 3D-фильтр может перемещаться во всех трех направлениях (высота, ширина, канал изображения) . В каждой позиции поэлементное умножение и сложение дают одно число.Поскольку фильтр скользит по трехмерному пространству, выходные числа также располагаются в трехмерном пространстве. В результате получается 3D-данные.
Подобно двумерным сверткам, которые кодируют пространственные отношения объектов в двухмерной области, трехмерные свертки могут описывать пространственные отношения объектов в трехмерном пространстве. Такие трехмерные отношения важны для некоторых приложений, таких как трехмерные сегментации / реконструкции биомедицинских изображений, например, КТ и МРТ, где такие объекты, как кровеносные сосуды, блуждают в трехмерном пространстве.
Поскольку мы говорили о глубинной операции в предыдущем разделе трехмерной свертки, давайте рассмотрим еще одну интересную операцию, 1 х 1 свертки.
Вы можете удивиться, почему это полезно. Мы просто умножаем число на каждое число во входном слое? Да и нет. Операция тривиальна для слоев только с одним каналом. Там мы умножаем каждый элемент на число.
Вещи становятся интересными, если входной слой имеет несколько каналов. На следующем рисунке показано, как свертка 1 x 1 работает для входного слоя с размером H x W x D.После свертки 1 x 1 с размером фильтра 1 x 1 x D выходной канал имеет размерность H x W x 1. Если мы применим N таких сверток 1 x 1, а затем объединяем результаты вместе, мы можем получить выходной слой с размером H x W x N.
Свертка 1 x 1, где размер фильтра равен 1 x 1 x D.
Изначально в документе «Сеть в сети» были предложены свертки 1 x 1. Затем они широко использовались в документе Google Inception. Несколько преимуществ сверток 1 x 1:
- Уменьшение размерности для эффективных вычислений
- Эффективное низкоразмерное встраивание или объединение признаков
- Повторное применение нелинейности после свертки
Первые два преимущества можно наблюдать на изображении выше.После 1 х 1 свертки мы значительно уменьшаем размер по глубине. Скажем, если исходный вход имеет 200 каналов, свертка 1 x 1 объединит эти каналы (функции) в один канал. Третье преимущество заключается в том, что после свертки 1 x 1 может быть добавлена нелинейная активация, такая как ReLU. Нелинейность позволяет сети изучать более сложные функции.
Эти преимущества были описаны в первоначальной статье Google как:
«Одна большая проблема с вышеупомянутыми модулями, по крайней мере, в этой наивной форме, состоит в том, что даже скромное число сверток 5×5 может быть чрезмерно дорогим на вершине сверточного слоя с большим количеством фильтров.
Это приводит ко второй идее предлагаемой архитектуры: разумно применять сокращения размеров и проекции везде, где вычислительные требования слишком сильно возрастут, в противном случае. Это основано на успехе вложений: даже низкоразмерные вложения могут содержать много информации об относительно большом патче изображения … То есть, 1 x 1 свертки используются для вычисления сокращений до дорогих сверток 3 x 3 и 5 x 5. Помимо использования в качестве сокращений, они также включают использование выпрямленной линейной активации, что делает их двойным назначением.
Одна интересная перспектива в отношении свертки 1 x 1 исходит от Янна ЛеКуна: «В сверточных сетях не существует такого понятия, как« полностью соединенные слои ». Есть только уровни свертки с ядрами свертки 1×1 и полной таблицей соединений ».
Теперь мы знаем, как бороться с глубиной в свертке. Давайте поговорим о том, как обрабатывать свертку в двух других направлениях (высота и ширина), а также о важной арифметике свертки.
Вот несколько терминов:
- Размер ядра: ядро обсуждалось в предыдущем разделе.Размер ядра определяет поле зрения свертки.
- Stride: определяет размер шага ядра при скольжении по изображению. Шаг 1 означает, что ядро скользит по изображению попиксельно. Шаг 2 означает, что ядро скользит по изображению, перемещаясь на 2 пикселя за шаг (т.е. пропуская 1 пиксель). Мы можем использовать шаг (> = 2) для уменьшения изображения.
- Заполнение: отступ определяет способ обработки границы изображения. Свернутая свертка («то же» заполнение в Tensorflow) будет сохранять пространственные размеры вывода равными входному изображению, добавляя 0 вокруг входных границ, если это необходимо.С другой стороны, незакрашенная свертка («действительное» заполнение в Tensorflow) выполняет свертку только для пикселей входного изображения, не добавляя 0 вокруг входных границ. Выходной размер меньше входного размера.
Эта следующая иллюстрация описывает двумерную свертку с использованием размера ядра 3, шага 1 и отступа 1.
Существует отличная статья о подробной арифметике («Руководство по арифметике свертки для глубокого обучения»). Можно обратиться к нему для подробных описаний и примеров для различных комбинаций размера ядра, шага и отступов.Здесь я просто суммирую результаты для самого общего случая.
Для входного изображения с размером i, размером ядра k, отступом p и шагом s выходное изображение из свертки имеет размер o:
Для многих приложений и во многих сетевых архитектурах мы часто хотим сделать преобразования, идущие в направлении, противоположном нормальной свертке, т.е. мы хотели бы выполнить повышающую дискретизацию. Несколько примеров включают в себя генерацию изображений с высоким разрешением и отображение карты низкоразмерных объектов в пространство больших размеров, например, в авто-кодере или семантической сегментации.(В последнем примере семантическая сегментация сначала извлекает карты характеристик в кодере, а затем восстанавливает исходный размер изображения в декодере, чтобы он мог классифицировать каждый пиксель в исходном изображении.)
Традиционно можно добиться повышения дискретизации путем применения Схемы интерполяции или создание правил вручную. Современные архитектуры, такие как нейронные сети, с другой стороны, позволяют самой сети автоматически обучаться правильному преобразованию без вмешательства человека. Чтобы достичь этого, мы можем использовать транспонированную свертку.
Транспонированная свертка также известна как деконволюция или дробно свернутая свертка в литературе. Тем не менее, стоит отметить, что название «деконволюция» является менее подходящим, поскольку транспонированная свертка не является реальной деконволюцией, как определено при обработке сигнала / изображения. Технически говоря, деконволюция в обработке сигналов полностью изменяет операцию свертки. Это не тот случай, здесь. Из-за этого некоторые авторы категорически против называть транспонированную свертку деконволюцией.Люди называют это деконволюцией в основном из-за простоты. Позже мы увидим, почему называть такую операцию транспонированной сверткой естественным и более уместным.
Всегда можно реализовать транспонированную свертку с прямой сверткой. Для примера на изображении ниже мы применяем транспонированную свертку с ядром 3 x 3 над входом 2 x 2, дополненным границей нулей 2 x 2, используя единичные шаги. Выход с повышенной дискретизацией имеет размер 4 x 4.
Повышение частоты дискретизации с входа 2 x 2 до выхода 4 x 4.Изображение взято из этой ссылки.
Интересно, что можно сопоставить одно и то же входное изображение 2 x 2 с другим размером изображения, применяя причудливые отступы и шаг. Ниже транспонированная свертка применяется к тому же входу 2 x 2 (с 1 нулем, вставленным между входами), дополненным 2 x
.
Как сделать пирамиду из картона

Хотите узнать, как делать поделки из картона? Этот материал предоставляет бесконечные возможности … Вам просто нужно следовать этим пошаговым инструкциям в этой статье, и вы узнаете, как сделать из пирамиды из картона . Это ремесло легко и быстро сделать. Это занятие, которое дети будут любить, и они также будут развлекаться, создавая их. Вы можете сделать несколько пирамид , изменив цвет картона .Попробуйте и посмотрите, как это просто!
шагов, чтобы следовать:
1
Первый шаг к созданию пирамиды — нарисовать на картоне сетку из девяти квадратов размером 8 см х 8 см (3,5 х 3,5 дюйма). Смотрите изображение.

2
Отметьте середину каждой стороны квадрата, как на картинке.

3
Нарисуйте форму пирамиды на картоне . Помните, что вы должны вести себя по квадратам.Убедитесь, что вы также отметили швы, которые должны быть на расстоянии около 0,5 см от исходной линии. Внимательно посмотрите на картинку ниже.

4
Разрезать картонную пирамиду .

5
Сложите все прекращенные линии, чтобы создать швы. Посмотрите на картинку ниже, чтобы увидеть, как должна выглядеть ваша пирамида.

6
Нанесите клей на боковые клапаны картонной пирамиды .

7
Склейте части пирамиды вместе с каждым клапаном и нажмите так, чтобы они прилипали со всех сторон. Вы закончили свою картонную пирамиду .

Если вы хотите прочитать похожие статьи на Как сделать пирамиду из картона , мы рекомендуем вам посетить нашу категорию Искусство и ремесло.
Советы
- Вы можете делать разные пирамиды, меняя цвет картона. Вы также можете делать пирамиды разных размеров, вам просто нужно сделать сетку больше или меньше.Вы также можете нарисовать на каждой стороне пирамиды или наклеить красочные картонные круги.
,
Any Queries? Ask us a question at +0000000000
