Треугольник объемный из бумаги схема: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника ✅ igrad.su

by alexxlab Posted in Разное on 31.05.201909.08.2020

Содержание

Объемные фигуры из картона выкройки. Геометрические фигуры из бумаги своими руками с описанием и фото схем

Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.

Как сделать объемные геометрические фигуры

Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.

Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.

Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.

Из бумаги

Из картона

Развертки куба

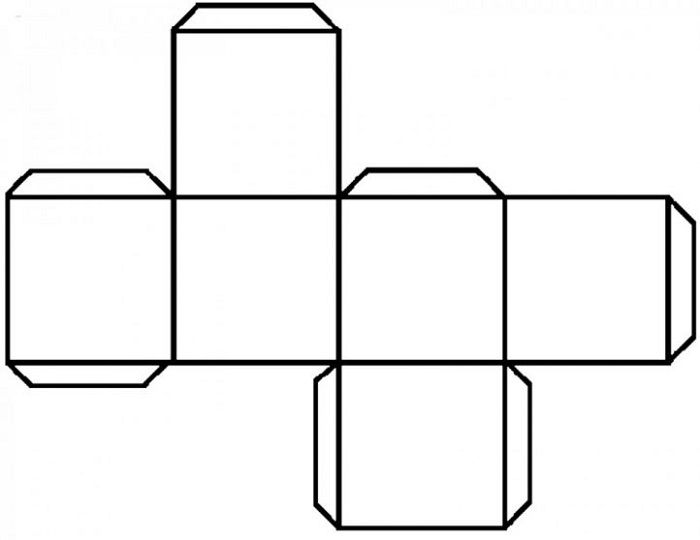
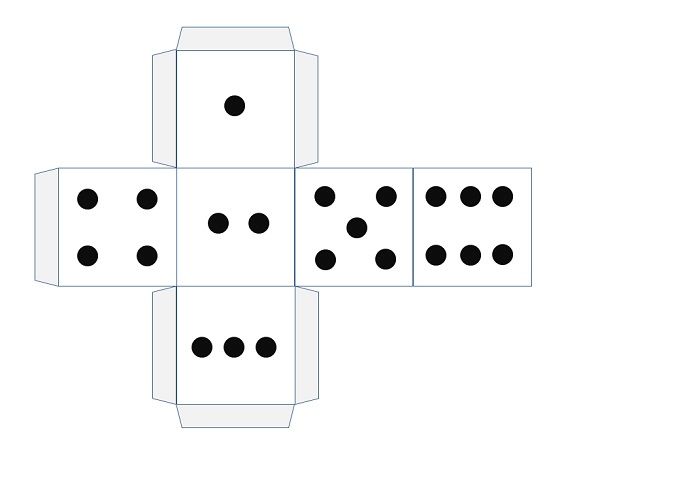
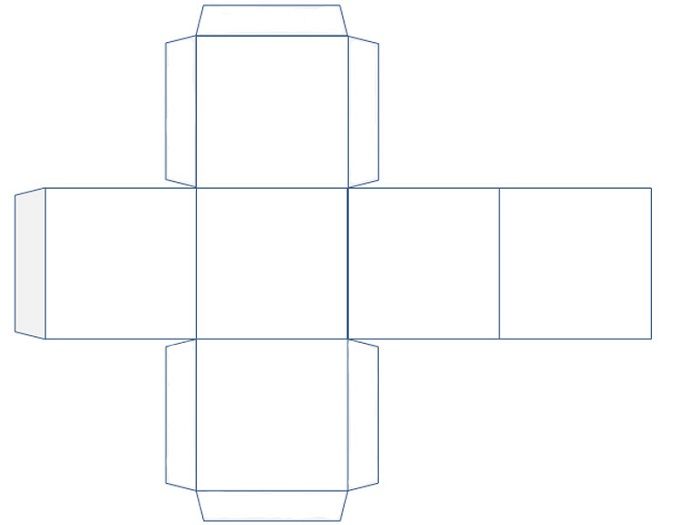
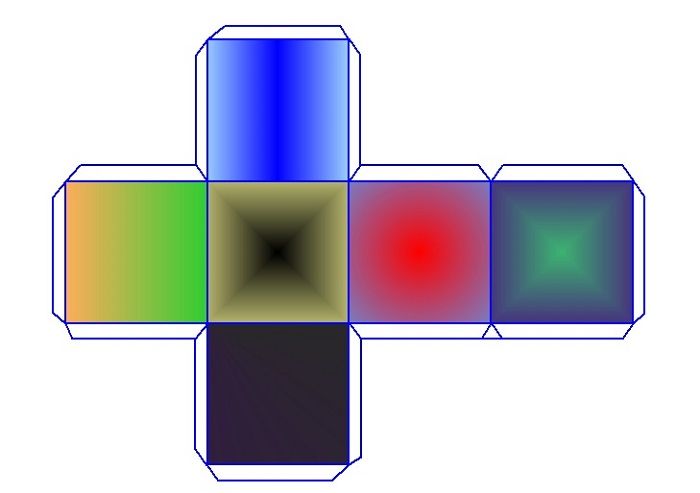
Треугольника

Прямоугольника

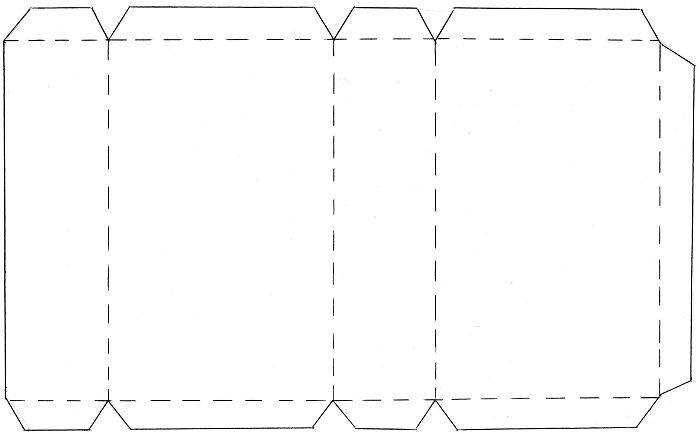
Цилиндра

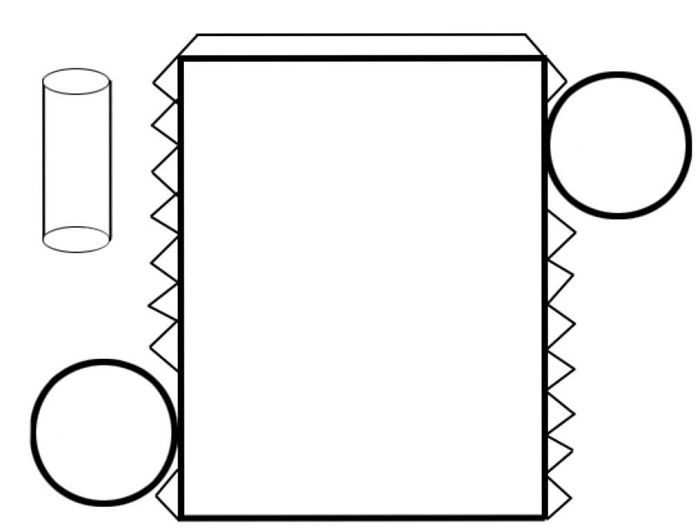
Ромба

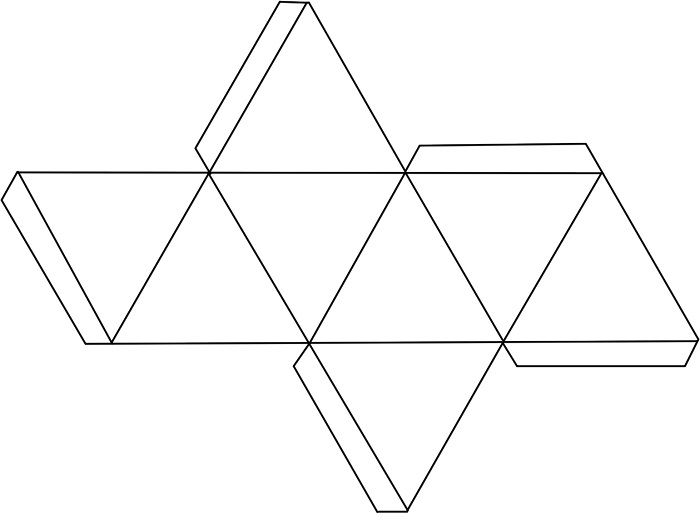
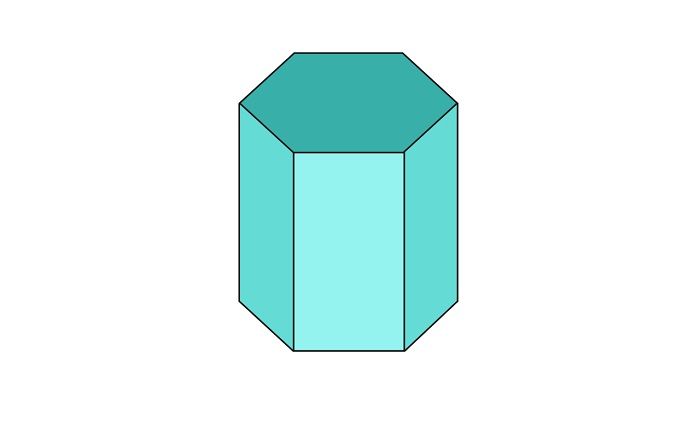
Призмы

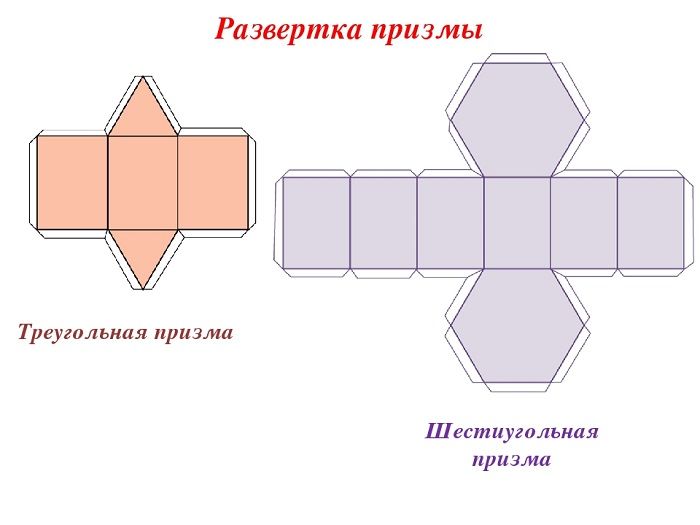
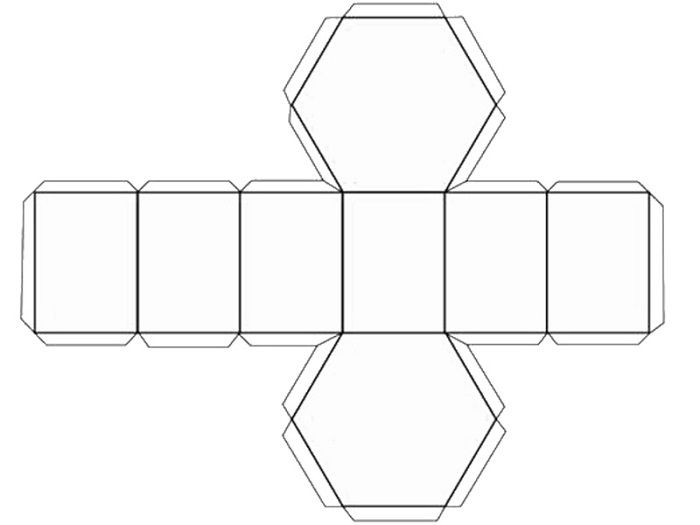
Схемы для вырезания

Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.

Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными

Треугольник | Базовая форма оригами

Когда мы начинаем любое новое для себя дело, то хотим знать правила работы и какие-либо условные знаки или символы. У каждой науки существует своя азбука.

В оригами также существует определенный набор азбучных знаний и терминов.

Если мы знаем эту азбуку, то мы не только легко сложим любую фигурку, но и зарисуем любую схему. Потом мы сможем воплотить ее в жизнь.

Автор этой своеобразной азбуки – японец Акира Йошизава. Он занимался этим в середине 20-го века.

С тех пор этой азбукой оригами пользуются оригамисты во всем мире. Начинается эта азбука с базовых форм оригами.

В этом видео уроке я показываю как сделать самую простую из них – “треугольник”. Эта форма, как и все другие, является основой бесчисленного множества фигурок оригами, а также является основой других базовых форм.

Например, на основе этого “треугольника” складывается стаканчик – практичная вещь для дома и создания поделок.

Когда же одна базовая форма является основой другой, то такое явление называют наложением базовых форм в оригами. Подробнее о наложении или превращениях в оригами в этом уроке.

Итак, для складывания “треугольника” возьмите квадратный лист бумаги и сложите его ровно пополам по диагонали. Получится треугольник или квадрат, сложенный пополам по диагонали.

На фото треугольник сложен из квадратного листа бумаги размером 10 * 10 см.

Посмотрите видео, как складывается эта базовая форма оригами:

Напишите в комментариях под уроком какие у вас успехи в складывании одной из первых базовых форм в оригами, либо свои пожелания, вопросы!

Поделитесь результатом на странице Вконтакте!

Понравился урок? Поделитесь им!

Удачи!

своими руками из бумаги :: SYL.ru

Придумано несколько невозможных фигур — лестница, треугольник и х-зубец. Эти фигуры на самом деле в объемном изображении вполне реальны. Но когда художник проектирует объем на бумагу, объекты кажутся невозможными. Треугольник, который еще носит название «трибар», стал замечательным примером того, как невозможное становится возможным, когда прикладываешь усилия.

Все эти фигуры — прекрасные иллюзии. Достижения человеческого гения используют художники, которые рисуют в стиле имп-арт.

Треугольник Пенроуза. Что это такое?

Нет ничего невозможного. Так можно сказать про треугольник Пенроуза. Это геометрически невозможная фигура, элементы которой не могут быть соединены. Все-таки невозможный треугольник стал возможным. Шведский живописец Оскар Реутерсвард в 1934 г. представил миру невозможный треугольник из кубиков. О. Реутерсвард считается первооткрывателем этой зрительной иллюзии. В честь этого события на почтовой марке Швеции напечатали позже этот рисунок.

А в 1958 г. математиком Роджером Пенроузом была напечатана публикация в английском журнале о невозможных фигурах. Именно он создал научную модель иллюзии. Роджер Пенроуз был невероятным ученым. Он проводил исследования в области теории относительности, а также увлекательной квантовой теории. Его наградили премией Вольфа совместно с С. Хокингом.

Известно, что художник Мауриц Эшер, находясь под впечатлением этой статьи, нарисовал свою изумительную работу — литографию «Водопад». Но возможно ли сделать треугольник Пенроуза? Как сделать, если это возможно?

Трибар и реальность

Хоть и фигура считается невозможной, сделать треугольник Пенроуза своими руками — легче простого. Его можно сделать из бумаги. Любители оригами просто не могли обойти стороной трибар и нашли все же способ создать и подержать в руках вещь, которая казалась ранее запредельной фантазией ученого.

Однако нас обманывают собственные глаза, когда мы смотрим на проекцию трехмерного объекта из трех перпендикулярных линий. Наблюдателю кажется, что он видит треугольник, хотя на самом деле это не так.

Геометрия поделки

Треугольник трибар, как сказано, на самом деле треугольником не является. Треугольник Пенроуза — иллюзия. Лишь под определенным углом объект выглядит как равносторонний треугольник. Однако объект в натуральном виде — это 3 грани куба. На такой изометрической проекции совпадают на плоскости 2 угла: ближний от зрителя и дальний.

Оптический обман, конечно, быстро раскрывается, лишь только взять этот объект в руки. А еще раскрывает иллюзию тень, так как тень трибара ясно показывает, что углы не совпадают в реальности.

Трибар из бумаги. Схемы

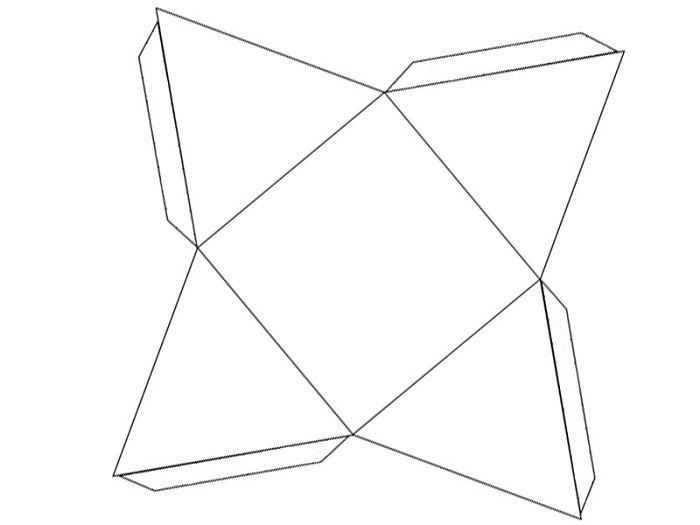
Как сделать треугольник Пенроуза своими руками из бумаги? Есть ли схемы этой модели? На сегодня изобретены 2 разверстки для того, чтоб сложить такой невозможный треугольник. Основы геометрии подсказывают, как именно складывать объект.

Чтобы сложить треугольник Пенроуза своими руками, понадобится выделить всего 10–20 минут. Нужно подготовить клей, ножницы для нескольких разрезов и бумагу, на которой печатается схема.

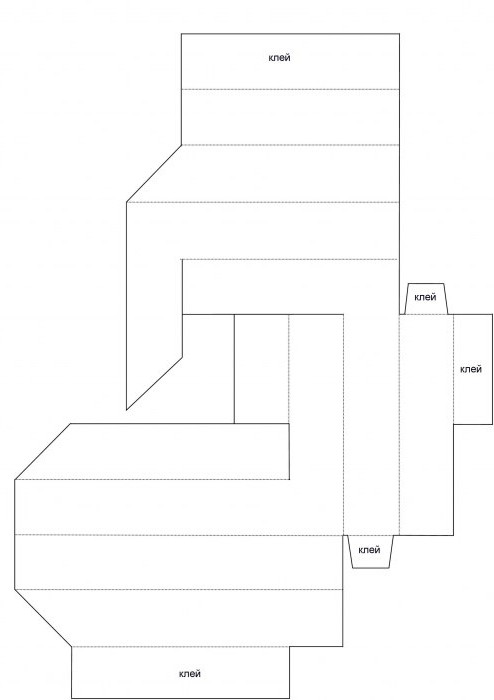Из такой заготовки получается самый популярный невозможный треугольник. Поделка-оригами не слишком сложна в изготовлении. Поэтому получится обязательно с первого раза, причем даже у школьника, только начавшего изучать геометрию.

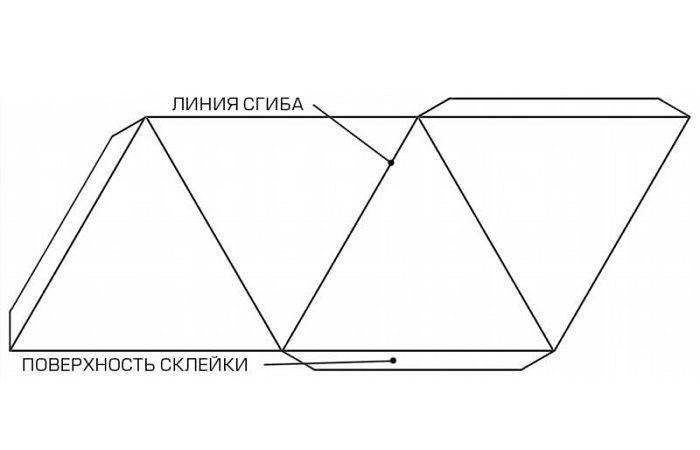
Как видим, получается очень симпатичная поделка. Вторая заготовка выглядит иначе и складывается по-другому, но сам треугольник Пенроуза в итоге выглядит так же.

Этапы создания треугольника Пенроуза из бумаги.

Выберите одну из 2 удобных для вас заготовок, скопируйте файл и распечатайте. Приведем здесь пример и второй модели разверстки, которая выполняется немного проще.

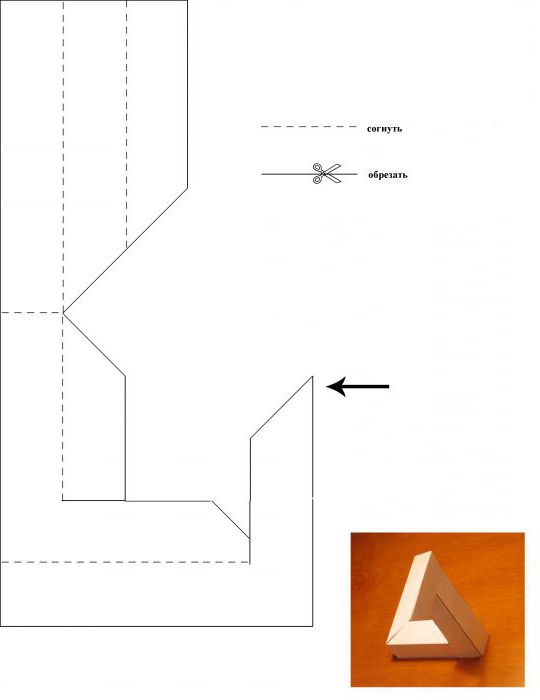Сама заготовка для оригами «Трибар» уже содержит все необходимые подсказки. По сути, инструкция к схеме не требуется. Достаточно только скачать на плотный бумажный носитель, иначе работать будет неудобно и фигура не получится. Если нельзя сразу распечатать на картоне, то требуется приложить эскиз к новому материалу и по контуру вырезать чертеж. Для удобства можно скрепить скрепками.

Что делать затем? Как сложить треугольник Пенроуза своими руками поэтапно? Нужно следовать такому плану действий:

Наводим обратной стороной ножниц те линии, где нужно согнуть, согласно инструкции. Сгибаем все линии
Там, где нужно, делаем разрезы.
Склеиваем с помощью ПВА те лоскутки, что предназначены для скрепления детали в единое целое.

Готовую модель можно перекрасить в любой цвет, или заранее взять для работы цветной картон. Но даже если объект будет из белой бумаги, все равно, все, кто входит в вашу гостиную впервые, будут непременно обескуражены такой поделкой.

Рисунок треугольника

Как нарисовать треугольник Пенроуза? Не все любят заниматься оригами, но многие обожают рисовать.

Для начала изображается обычный квадрат любого размера. Затем внутри рисуется треугольник, основой которого является нижняя сторона квадрата. В каждый угол вписывается небольшой прямоугольник, все стороны которого стираются; остаются лишь те стороны, что примыкают к треугольнику. Это необходимо, чтобы линии были ровными. Получается треугольник с усеченными углами.

Следующий этап — изображение второго измерения. От левой части верхнего нижнего угла проводится строго прямая линия. Такая же линия проводится, начиная с нижнего левого угла, и немного не доводится до первой линии 2 измерения. Еще одна линия рисуется с правого угла параллельно нижней стороне основной фигуры.

Заключительный этап — внутри второго измерения рисуется третье с помощью еще трех небольших линий. Маленькие линии начинаются от линий второго измерения и завершают образ трехмерного объема.

Другие фигуры Пенроуза

По такой же аналогии можно нарисовать и иные фигуры — квадрат либо шестиугольник. Иллюзия будет соблюдаться. Но все же эти фигуры уже не так потрясают воображение. Такие многоугольники кажутся просто сильно перекрученными. Современная графика позволяет сделать и более интересные версии знаменитого треугольника.

Кроме треугольника, всемирно известна еще и лестница Пенроуза. Идея состоит в обмане зрения, когда кажется, что человек поднимается непрерывно вверх при движении по часовой стрелке, а если движется против часовой стрелки, то вниз.

Непрерывная лестница известна больше по ассоциации с картиной М. Эшера «Восхождение и спуск». Интересно, что, когда человек проходит все 4 пролета этой иллюзорной лестницы, он неизменно оказывается там, откуда начинал.

Известны и другие объекты, вводящие разум человека в заблуждение, такие как невозможный брусок. Или сделанный по тем же законам иллюзии ящик с пересекающимися гранями. Но все эти объекты уже придуманы на основе статьи замечательного ученого — Роджера Пенроуза.

Невозможный треугольник в Перте

Фигуре, названной в честь математика, оказана честь. Ей установлен памятник. В 1999 году в одном из городов Австралии (Перт) установлен большой треугольник Пенроуза из алюминия, который составляет 13 метров в высоту. Рядом с алюминиевым гигантом с удовольствием фотографируются туристы. Но если выбрать для фотографии другой угол зрения, то обман становится очевидным.

Как сделать пирамиду из бумаги. Схема с размерами, пошаговая инструкция с фото

Если вас интересует, как сделать идеальную по формам и граням пирамиду из бумаги существует определенная схема с размерами, чтобы в итоге получилась правильная фигура. Бумажная пирамида может быть оригинальным подарком, сделанным своими руками или просто интересной поделкой.

Как сделать пирамиду из бумаги. Пошаговая инструкция

Благодаря древнему мастерству оригами есть возможность воссоздавать практически любую фигуру из бумаги, в том числе и пирамиду. Существует несколько способов, как создать идеальную фигуру с четкими гранями. Для новичков в этом деле есть легкий пошаговый совет, как сделать фигуру из картона. Данная инструкция будет понятна как взрослым, так и детям.

Пошаговое руководство, как склеить пирамиду из картона:

На бумажном листе нужно нарисовать один ровный квадрат и три треугольника. Каждая сторона квадрата должна быть примерно 15 см. Ширину треугольника стоит сделать такой же, а высоту 27 см.
Ножницами вырезать заготовки не по контуру, а с отступом 3-4 мм, в дальнейшем это будет необходимо при склеивании фигуры.
Смазать клеем все части, дать ему немного подсохнуть и сложить все детали в единую конструкцию.
Дать полностью высохнуть поделке и можно приступить к декору.

Как украсить пирамиду — может быть любая воля фантазии. Например, на нее можно наклеить фигурки, обмотать фольгой или раскрасить специальными акриловыми красками.

Материалы и приспособления

Как сделать пирамиду из бумаги схема с размерами – не единственные главные составляющие в изготовлении фигуры.

Для удобства выполнения оригами следует заранее подготовить необходимые материалы и приспособления, чтобы в момент работы все они были под рукой:

Для изготовления граней могут понадобиться различные материалы. Задействовать можно не только картон, но и пластик, металл, фанеру, стекло или сделать каркас из проволоки. Если фигура создана с каким-либо эзотерическим посылом, то бумажную пирамиду советуется изнутри обклеить фольгой. Это нужно для того чтобы в фигуре накапливалась и не рассеивалась положительная энергия. Если внутрь пирамиды поместить несколько небольших магнитов, то изделие будет обладать магнитной энергией.
Для поделки стоит обзавестись качественным клеем, который можно купить в канцелярском магазине.
Пригодятся острые ножницы, чтобы вырезать ровные заготовки для будущей фигуры.
Также нужны будут линейка, карандаш и ластик на всякий случай.

Для выполнения фигуры не требуется много материалов, все приспособления для пирамиды найдутся почти в каждом доме.

Определяем параметры

Чтобы изделие получилось аккуратным и красивым стоит задать четкие параметры при изготовлении заготовок для будущей пирамиды. Для каждой части может понадобиться отдельный лист бумаги. Можно скачать уже готовые схемы, но их также просто нарисовать самостоятельно.

Главное знать, что ширина треугольника должна быть равна каждой длине грани квадрата.

Высоту геометрической фигуры можно выбрать любую, но рекомендуемая длина, чтобы она была больше на 10-15 см ширины заготовки. Именно при таком соотношении фигура будет смотреться гармонично.

Строим чертеж

Чтобы было проще узнать, как сделать идеальную пирамиду из бумаги или каких-либо других материалов существует схема с размерами. Чертеж – основа для дальнейшего склеивания компонентов для будущей цельной фигуры. Существует несколько видов пирамид, для каждой из них свой чертеж.

Но есть один простой способ, который подходит для детей и новичков в этом деле:

В основании пирамиды должен быть правильный многоугольник, с проходящий высотой через его центр. Заранее стоит определить размеры пирамиды, для каждого они могут быть индивидуальны.
Нужно нарисовать четыре квадрата, три из них будут нужны для треугольников.
На одной из боковых сторон нужно определить середину линии. От двух углов основания следует провести две линии в отмеченную точку, чтобы получилась вершина пирамиды.
Заготовки равнобедренных треугольников нужно будет соединить с квадратом с помощью специальных отступов. Стоит не забыть, что вырезать заготовки нужно прибавив к их краям полсантиметра для того чтобы было удобно склеить фигуру.

Завершение моделирования

Вырезанную фигуру, нужно склеить по линиям сгибов. Перед тем как соединить части в полную модель на сгибы нужно нанести клей и немного оставить его застыть, чтобы он лучше схватился. После того как изделие будет готово следует его оставить на полчаса, чтобы потом при оформлении оно случайно не расклеилось. В завершающий этап моделирования входит дизайнерское оформление работы.

Можно разукрасить пирамиду акриловыми или мерцающими красками, нарисовать на ней фигуры.

Изделие можно обклеить фольгой или бумагой для подарков. Также для тех, кто верит в мистическую силу пирамиды стоит на нее приклеить натуральные камни, которые будут подходить под знак зодиака того, кому будет подарена данная фигура. В детском варианте пирамиду можно превратить в животное, приклеив к ней ушки, хвостик и нарисовать черты мордочки.

Способ 2

Такая схема пирамиды подразумевает использование готовой заготовки, которую можно скачать и распечатать на принтере. Этот вариант самый простой, так как не придется чертить фигуры самостоятельно. Главное подготовить все необходимые инструменты и оригинально украсить изделие на этапе декорирования.

Способ 3

Существует достаточно много советов, как сделать пирамиду из бумаги, определенная схема с размерами является неотъемлемой частью в выполнении оригами:

Квадратный лист сложить, чтобы углы лежали противоположно друг к другу, лишнюю бумагу отрезать ножницами. Таким способом можно сделать ровный квадрат.
Заготовку свернуть по одной диагонали, раскрыть и свернуть по другой и снова развернуть. Так намечаются нужные линии.
Взять половинки квадрата, свернуть из него треугольник в два слоя. К центру свернуть два угла от основания. Аналогично повторить со второй стороны фигуры.
Согнуть уголки к центру с одной стороны и с другой.
Разогнуть ромб с каждой стороны, уголки его направить внутрь.
Пирамиду нужно выгнуть так чтобы получилась звезда с четырьмя гранями. Фигуру взять двумя руками за разные концы и придать ей форму.

Постепенно придавая объекту форму, начнет получаться пирамида. Очень важно знать, что на последнем этапе нужно действовать аккуратно, стараясь не порвать случайно поделку.

Способ 4

Необходимые инструменты для поделки:

бумажный лист,
треугольник,
ножницы,
карандаш,
клей,
ластик.

Выполнение:

Вырезать квадрат. Согнуть заготовку пополам в разные стороны, чтобы образовались складки.
Диагональ треугольника приложить к каждой из сторон квадрата и по сгибам сделать отметки.
При помощи линий соединить треугольник с вершинами. Для точности рекомендуется использовать линейку.
Отметить карандашом линии склейки сторон.
Фигуру вырезать и нанести клей на линии склеивания.

Как сделать пирамиду из картона?

Сделать фигуру из картона своими руками можно быстро и просто. Использовать можно любую расцветку бумаги, но лучше всего подойдет цвет золота, бежевый, светло-коричневый.

Для того чтобы изделие выглядело более реалистично, то по бумажной заготовке можно произвести линии иголкой горизонтальные и вертикальные.

Благодаря этому будет создаваться эффект реальной мини-пирамиды из Гизы.

По вышеперечисленным пошаговым способам можно создать фигуру с гранями. Картонная пирамида делается по такому же принципу как из простой бумаги.

Но есть большой плюс, что ее можно украсить, например сахарным песком:

Изделие можно покрыть полностью прозрачным клеем и нанести на него сахарный песок. Таким способом можно создать интересный сияющий эффект.
Также пирамиду можно посыпать песком, предварительно обмазав ее клеем. Фигура приобретет эффект реалистичности.

«Золотое сечение» в пропорциях пирамиды

Эталон идеальной пирамиды – определенные правильные пропорции. Ключом к созданию правильной фигуры лежит коэффициент и цифры 7,23. Число, которое имеет значение в науке математике и геометрии, также эти цифры важны в архитектуре и даже медицине.

Отрезок длиной 7,23 нужно умножить на коэффициент 1,618. Полученное число 116, 981 следует округлить до 117 см. Эта длина является основанием пирамиды.

Также для получения больших моделей данное число можно умножать в несколько раз. Таким образом, длина нашей пирамиды получается 117 мм, а высота 72 мм.

По теореме Пифагора можно определить длину граней треугольника. Получится число 92,769, его нужно округлить до 93. Эти данные подстроены под идеальную пропорцию «Золотого сечения».

Как сделать развертку четырехугольной пирамиды?

Для изготовления четырехугольной фигуры потребуется:

плотная бумага или картон,
простой карандаш,
линейка,
ножницы,
клей.

Этапы:

Для начала нужно сделать выкройку, в которой основание будет 8 см, а высота 6,5 см.
На листе бумаги нужно нарисовать ровный квадрат, отметить на каждой его грани середину.
Провести из средних точек линии перпендикулярно квадрату, длиной 6,5 см — их всего должно получиться 4.
Из каждой вершины провести по две линии к углам квадрата, так чтобы получились треугольники.
Вырезать заготовку и сложить треугольники так чтобы они сошлись в единую вершину. Склеить фигуру.

Четырехугольную фигуру несложно изготовить самостоятельно. Также на основе этой пошаговой инструкции можно создавать пирамиды больше по размерам.

Как выполнить развертку правильной пирамиды?

Чтобы понимать как сделать пирамиду из бумаги, необходимо знать схему с размерами.

Если интересно как сделать пирамиду с разверткой из бумаги, существует не одна схема с размерами, которая поможет правильно выполнить фигуру. В момент проектирования развертки за основу берется правильный треугольник. Боковая поверхность представлена как плоский чертеж, состоящий из граней и многоугольника.

Для начала определяется натуральная величина основания и истинная величина всех ребер (можно произвести при помощи циркуля). После того как три стороны были найдены строится основание и боковая грань. Берется произвольная точка и из нее проводится дуга равная длине боковых ребер заготовки. На дуге отмечаются четыре отрезка, равные основанию пирамиды.

Все линии соединяются, в том числе с произвольной точкой. К одному из получившихся треугольников пририсовывают квадрат, который равен основанию фигуры.

Сложные фигуры: объемные макеты

Фигуры такого типа делаются для получения навыков в работе с объемными изделиями из бумаги и в целях обучения детей начальным азам геометрии. Из таких моделей можно смастерить оригинальную подарочную упаковку. Иногда бывает сложно разработать правильную развертку, рекомендуется обладать хотя бы небольшими знаниями черчения.

Но существуют готовые трафареты, которые можно будет распечатать с принтера. Макеты используются не только в развлекательных целях, но и в обучающих. Ребенку можно наглядно показывать, как выглядит та или иная фигура. Сложные модели могут быть: куб, октаэдр, додекаэдр, икосаэдр и другие.

Перед тем как начать выполнять черчение фигуры стоит представить ее в 3D формате, сколько она имеет граней и измерений.

На листе бумаги нужно нарисовать грани, так чтобы они между собой правильно соединялись. У каждой фигуры есть свой определенный тип грани. Ребра тоже должны быть одинаковой длины, чтобы при скреплении не появились несостыковки. Если макет имеет одинаковые стороны, то в момент черчения можно нарисовать шаблон и по нему рисовать остальные заготовки.

3D макеты важны при обучении детей: они дают ученикам возможность подержать фигуры в руках, рассмотреть их и лучше понять строение. Также при изучении некоторых теорем (Эйлера) рекомендуется наглядное пособие.

Моделирование различных многогранников

Чтобы научиться выполнять более сложные модели, стоит начать с азов, например, с 3D треугольников. Постепенно улучшая навык в создании простых макетов можно приступить к сложным моделям. Сложные фигуры требуют навыков и отточенной сноровки при выполнении, например в момент развертки или придавания формы фигуре, нужно действовать так чтобы она случайно не порвалась.

При выполнении чертежа следует внимательно наносить разметки и уметь рисовать фигуры.

Если есть вопрос, как сделать качественную пирамиду из бумаги, существует подробная схема с индивидуальными размерами. Стоит лишь приложить немного усилий, и тогда составит труда выполнить красивую и качественную работу, которая будет радовать глаз.

Благодаря вышеперечисленным способам можно легко создать различные макеты пирамид. Не сложно научиться выполнять эти техники, главное соблюдать все этапы постепенно и внимательно.

Видео о том, как сделать пирамиду из бумаги

Как сделать пирамиду из бумаги, узнайте в видео-ролике:

Схема выполнения объемной пирамиды:

трехмерных фигур | SkillsYouNeed

На этой странице рассматриваются свойства трехмерных или «твердых» форм.

Двумерная фигура имеет длину и ширину. У трехмерной твердой формы тоже есть глубина. Трехмерные формы по своей природе имеют внутреннюю и внешнюю стороны, разделенные поверхностью. Все физические предметы, к которым можно прикоснуться, трехмерны.

Эта страница охватывает как твердые тела с прямыми сторонами, называемые многогранниками, которые основаны на многоугольниках, так и твердые тела с кривыми, такие как глобусы, цилиндры и конусы.

Многогранники

Многогранники (или многогранники) — это твердые тела с прямыми сторонами. Многогранники основаны на многоугольниках, двухмерных плоских формах с прямыми линиями.

См. Нашу страницу Свойства полигонов для получения дополнительной информации о работе с полигонами.

Многогранники определяются как имеющие:

Прямые кромки .
Плоские стороны называются гранями .
Углы, называемые вершинами .

Многогранники также часто определяются количеством ребер, граней и вершин, которые они имеют, а также тем, имеют ли их грани одинаковую форму и размер.Как и многоугольники, многогранники могут быть правильными (основанными на правильных многоугольниках) или неправильными (основанными на неправильных многоугольниках). Многогранники также могут быть вогнутыми или выпуклыми.

Один из самых простых и известных многогранников — это куб. Куб — это правильный многогранник, имеющий шесть квадратных граней, 12 ребер и восемь вершин.

Правильные многогранники (Платоновы тела)

Пять правильных тел. — это особый класс многогранников, все грани которых идентичны, причем каждая грань представляет собой правильный многоугольник.Платоновы тела:

Тетраэдр с четырьмя равносторонними треугольными гранями.
Куб с шестью квадратными гранями.
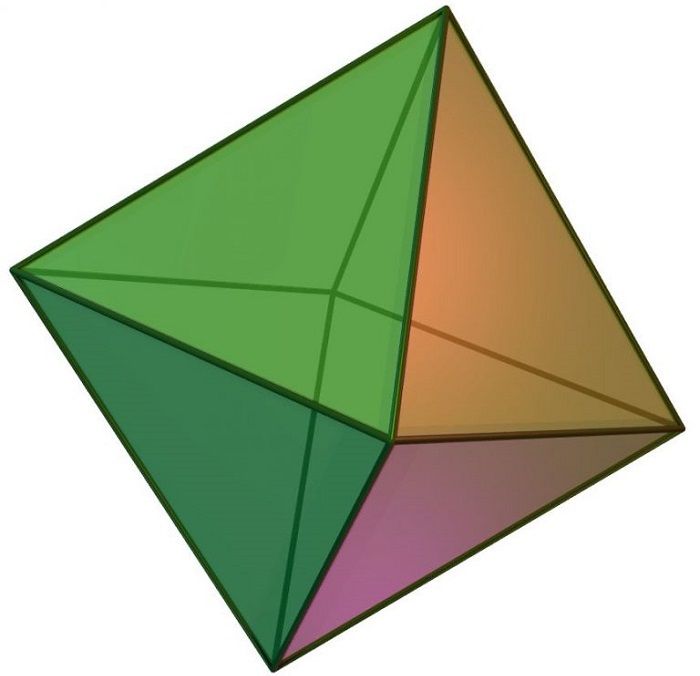
Октаэдр с восемью равносторонними треугольными гранями.
Додекаэдр с двенадцатью гранями пятиугольника.
Икосаэдр с двадцатью равносторонними треугольными гранями.

См. Диаграмму выше для иллюстрации каждого из этих правильных многогранников.

Что такое призма?

Призма — это любой многогранник, у которого есть два совпадающих конца и плоские стороны .Если вы разрежете призму в любом месте по ее длине, параллельно концу, ее поперечное сечение будет одинаковым — вы получите две призмы. Стороны призмы составляют параллелограммов — четырехгранных форм с двумя парами сторон равной длины.

Антипризмы похожи на обычные призмы, их концы совпадают. Однако стороны антипризм состоят из треугольников, а не параллелограммов. Антипризмы могут стать очень сложными.

Что такое пирамида?

Пирамида — это многогранник с основанием многоугольника , который соединяется с вершиной (верхняя точка) прямыми сторонами.

Хотя мы склонны думать о пирамидах с квадратным основанием, подобных тем, что строили древние египтяне, на самом деле они могут иметь любое основание многоугольника, правильное или неправильное. Кроме того, пирамида может иметь вершину в прямом центре своего основания, Правая пирамида , или может иметь вершину вне центра, когда это наклонная пирамида .

Более сложные многогранники

Есть еще много видов многогранников: симметричные и несимметричные, вогнутые и выпуклые.

Архимедовы тела, например , состоят как минимум из двух разных правильных многоугольников.

Усеченный куб (как показано) представляет собой архимедово твердое тело с 14 гранями. 6 граней — правильные восьмиугольники, а остальные 8 — правильные (равносторонние) треугольники. У фигуры 36 ребер и 24 вершины (угла).

Трехмерные фигуры с кривыми

Твердые фигуры с закругленными или закругленными краями не являются многогранниками. Многогранники могут иметь только прямые стороны.

Многие из окружающих вас объектов будут иметь по крайней мере несколько кривых. В геометрии наиболее распространенными изогнутыми телами являются цилиндры, конусы, сферы и торы (множественное число для тора).

Общие трехмерные формы с кривыми:
Цилиндр	Конус

Цилиндр имеет одинаковое поперечное сечение от одного конца до другого. Цилиндры имеют два одинаковых конца в форме круга или овала.Несмотря на то, что цилиндры похожи, цилиндры не являются призмами, поскольку призма имеет (по определению) параллелограмм с плоскими сторонами.	Конус имеет круглое или овальное основание и вершину (или вершину). Сторона конуса плавно сужается к вершине. Конус похож на пирамиду, но отличается тем, что конус имеет одну изогнутую сторону и круглое основание.
Сфера	Тор

Сфера в форме шара или земного шара представляет собой полностью круглый объект.Каждая точка на поверхности сферы находится на равном расстоянии от центра сферы.	В форме кольца, шины или пончика, регулярный кольцевой тор образуется путем вращения меньшего круга вокруг большего круга. Существуют также более сложные формы торов.

Площадь

На нашей странице «Расчет площади» объясняется, как рассчитать площадь двумерных фигур, и вам необходимо понимать эти основы для расчета площади поверхности трехмерных фигур.

Для трехмерных форм мы говорим о площади поверхности , чтобы избежать путаницы.

Вы можете использовать свои знания о площади двумерных форм для вычисления площади поверхности трехмерной формы, поскольку каждая грань или сторона фактически является двумерной формой.

Поэтому вы прорабатываете площадь каждой грани, а затем складываете их вместе.

Как и в случае плоских форм, площадь поверхности твердого тела выражается в квадратных единицах: см ², дюймы ², м ² и т. Д.Вы можете найти более подробную информацию об единицах измерения на нашей странице Системы измерения .

Примеры расчета площади поверхности

Куб

Площадь поверхности куба — это площадь одной грани (длина х ширина), умноженная на 6, потому что все шесть граней одинаковы.

Поскольку грань куба представляет собой квадрат, вам нужно выполнить только одно измерение — длина и ширина квадрата, по определению, одинаковы.

Следовательно, одна грань этого куба 10 × 10 см = 100 см ².Умножив на 6 количество граней куба, мы находим, что площадь поверхности этого куба равна 600 см ².

Другие правильные многогранники

Точно так же площадь поверхности других правильных многогранников (платоновых тел) может быть вычислена, если найти площадь одной стороны, а затем умножить ответ на общее количество сторон — см. Схему основных многогранников выше.

Если площадь одного пятиугольника, образующего додекаэдр, равна 22 см ², умножьте это на общее количество сторон (12), чтобы получить ответ 264 см ².

Пирамида

Для расчета площади поверхности стандартной пирамиды с четырьмя равными треугольными сторонами и квадратным основанием:

Сначала определите площадь основания (квадрата) длина × ширина.

Затем проработайте площадь одной стороны (треугольник). Измерьте ширину по основанию, а затем высоту треугольника (также известную как наклонная длина) от центральной точки основания до вершины.

Затем вы можете либо разделить полученный ответ на 2, чтобы получить площадь поверхности одного треугольника, а затем умножить на 4, чтобы получить площадь поверхности всех четырех сторон, либо просто умножьте площадь поверхности одного треугольника на 2.

Наконец, сложите площадь основания и стороны вместе, чтобы найти общую площадь поверхности пирамиды.

Чтобы вычислить площадь поверхности других типов пирамид, сложите площадь основания (известную как площадь основания) и площадь сторон (боковая площадь), вам может потребоваться измерить стороны по отдельности.

Диаграммы сети

Геометрическая сеть — это двухмерный «узор» для трехмерного объекта. Сетки могут быть полезны при определении площади поверхности трехмерного объекта.На диаграмме ниже вы можете увидеть, как строятся базовые пирамиды. Если пирамида «развернута», у вас остается сеть.

Призма

Для расчета площади поверхности призмы :

Призмы имеют два конца одинаковые и плоские стороны параллелограмма.

Вычислите площадь одного конца и умножьте на 2.

Для обычной призмы (у которой все стороны одинаковые) вычислите площадь одной из сторон и умножьте на общее количество сторон.

Для призм неправильной формы (с разными сторонами) рассчитайте площадь каждой стороны.

Сложите два ваших ответа (концы × стороны), чтобы найти общую площадь поверхности призмы.

Цилиндр

Пример:
Радиус = 5 см
Высота = 10 см

Чтобы рассчитать площадь поверхности цилиндра , полезно подумать о составных частях формы. Представьте банку сладкой кукурузы — у нее есть верх и низ, оба из которых представляют собой круги.Если отрезать сторону по длине и расплющить, получится прямоугольник. Поэтому вам нужно найти площадь двух кругов и прямоугольника.

Сначала проработайте область одного из кругов.

Площадь круга равна π (пи) × радиус ².

Предполагая радиус 5 см, площадь одного из кругов составляет 3,14 × 5 ² = 78,5 см ².

Умножьте ответ на 2, так как есть два круга 157см ²

Площадь стороны цилиндра равна периметру окружности, умноженному на высоту цилиндра.

Периметр равен π x 2 × радиус. В нашем примере 3,14 × 2 × 5 = 31,4

Измерьте высоту цилиндра — в этом примере высота составляет 10 см. Площадь поверхности стороны 31,4 × 10 = 314см ².

Общую площадь можно найти, сложив вместе площади кругов и стороны:

157 + 314 = 471 см ²

Пример:
Радиус = 5 см
Длина наклона = 10 см

Конус

При расчете площади поверхности конуса вам необходимо использовать длину «склона», а также радиус основания.

Однако вычислить относительно просто:

Площадь круга у основания конуса равна π (пи) × радиус ².

В этом примере сумма равна 3,14 × 5 ² = 3,14 × 25 = 78,5 см ²

Площадь боковой части, наклонного участка, можно найти по следующей формуле:

π (пи) × радиус × длина уклона.

В нашем примере сумма равна 3,14 × 5 × 10 = 157 см ².

Наконец, добавьте площадь основания к боковой области, чтобы получить общую площадь поверхности конуса.

78,5 + 157 = 235,5 см ²

Теннисный мяч:
Диаметр = 2,6 дюйма

Сфера

Площадь поверхности сферы — это относительно простое разложение формулы для площади круга.

4 × π × радиус ².

Для сферы часто легче измерить диаметр — расстояние по сфере. Затем вы можете найти радиус, равный половине диаметра.

Диаметр стандартного теннисного мяча 2.6 дюймов. Следовательно, радиус составляет 1,3 дюйма. Для формулы нам нужен квадрат радиуса. 1,3 × 1,3 = 1,69.

Следовательно, площадь теннисного мяча составляет:

4 × 3,14 × 1,69 = 21,2264 дюйма ².

Пример:
R (большой радиус) = 20 см
r (малый радиус) = 4 см

Тор

Чтобы вычислить площадь поверхности тора , необходимо найти два значения радиуса.

Большой или большой радиус (R) измеряется от середины отверстия до середины кольца.

Малый или малый радиус (r) измеряется от середины кольца до внешнего края.

На схеме показаны два вида примера тора и способы измерения его радиусов (или радиусов).

Расчет площади поверхности состоит из двух частей (по одной для каждого радиуса). Расчет одинаков для каждой детали.

Формула: площадь поверхности = (2πR) (2πr)

Для определения площади поверхности примера тора.

(2 × π × R) = (2 × 3.14 × 20) = 125,6

(2 × π × r) = (2 × 3,14 × 4) = 25,12

Умножьте два ответа вместе, чтобы найти общую площадь поверхности примера тора.

125,6 × 25,12 = 3155,072 см ².

Заполнение твердого тела: объем

Для трехмерных фигур вам также может потребоваться знать, какой объем они имеют.

Другими словами, если вы наполните их водой или воздухом, сколько наполнения вам потребуется?

Это описано на нашей странице Расчет объема .

Генератор двумерных качественных сеток и триангулятор Делоне

Triangle: Двухмерный качественный генератор сеток и
Триангулятор Делоне

riangle

Генератор двумерных качественных сеток и триангулятор Делоне.

Джонатан Ричард Шевчук
Отделение компьютерных наук
Калифорнийский университет в Беркли
Беркли, Калифорния 94720-1776

Победитель
2003
Премия Джеймса Харди Уилкинсона в области численного программного обеспечения.
Создано в Университете Карнеги-Меллона в рамках
проект Quake
(инструменты для моделирования крупномасштабных землетрясений).
Поддерживается NSERC
Стипендия 1967 года в области науки и техники и
Грант NSF CMS-9318163.

Треугольник генерирует точные триангуляции Делоне, ограниченные Делоне
триангуляции, соответствующие триангуляции Делоне, диаграммы Вороного и
качественные треугольные сетки. Последний может быть создан с помощью немалых
или большие углы, и поэтому подходят для анализа методом конечных элементов.

Triangle (версия 1.6, с Show Me версии 1.6) доступен как
файл .zip
(159K) или как
а .shar
файл (829K)
(извлечение с помощью sh)
из
Netlib в
Вороного
каталог.
Обратите внимание, что хотя Triangle находится в свободном доступе,
он защищен авторским правом автора и не может быть продан или включен в
коммерческие продукты без лицензии.

Новые функции в версии 1.6 (выпущенной 28 июля 2005 г.).
Улучшена обработка доменов с малыми углами
(благодаря алгоритму Гэри Миллера, Стивена Павла и Ноэля Уокингтона).В частности, Triangle теперь предлагает гарантию отсутствия больших углов.
даже для доменов с очень маленькими входными углами
(что делает невозможной гарантию немалого угла).
У сеток иногда меньше треугольников, чем в предыдущих версиях,
благодаря двум изменениям.
Во-первых, Triangle теперь использует алгоритм уточнения Делоне Пола Чу,
который более консервативен в отношении разделения сегментов, чем предыдущий
версии Triangle, когда угол составляет менее 30 градусов.
(Алгоритм Рупперта по-прежнему доступен через переключатель -D,
предлагая все-сетку Делоне.)
Во-вторых, изменение приоритета очереди плохих треугольников.
(предложено Альпером Юнгором) дает меньше треугольников
когда угол большой.
Исправлено много ошибок,
включая три ошибки, которые вызывали ошибки сегментации.
(Если вы используете Triangle версии 1.5, я настоятельно рекомендую вам немедленно заменить его.
Однако более ранние версии стабильны.)

Особый интерес.
Доступны две статьи о Треугольнике.
Эти и другие документы доступны на сайте
Страница кредита на исследование. треугольника
надежные геометрические предикаты доступны отдельно от
Страница надежных предикатов.Эти геометрические предикаты находятся в открытом доступе (хотя Triangle — нет).

Инструкция по использованию Triangle

Краткое заявление

Если вы используете треугольник, и особенно если вы используете его для выполнения
настоящая работа, я бы очень хотел услышать от вас. Короткое письмо или электронное письмо
(к)
описание того, как вы используете Triangle, будет много значить для
меня. Чем больше людей, которых я знаю, используют эту программу, тем легче мне будет
оправдать затраты времени на улучшения, которые, я надеюсь, принесут вам пользу.

Также дайте мне знать, если вы хотите, чтобы я внес вас в список для получения электронной почты
всякий раз, когда появляется новая версия Triangle или другой инструмент в
Цепь Архимеда, имеется.
Это , а не публичный
список; вы не получите электронную почту ни от кого, кроме меня, и не будете получать ее часто.
Не нужно бояться переполненного почтового ящика.

Если вы используете в публикации сетку, созданную с помощью Triangle, включите
также признание.
И, пожалуйста, пишите Треугольник с большой буквы!
Если вы хотите включить цитату из статьи,
Я предлагаю выбрать один из двух наверху
Страница кредита на исследование.

Чтобы узнать о других указателях создания сетки, взгляните на Роберта Шнайдера.

Страница создания сетки конечных элементов,

Страница генераторов сетки Роджера Янга

Каталог ресурсов по конечным элементам и каталог Стива Оуэна

Уголок исследования сетки.
Также Nina Amenta’s

Справочник программного обеспечения для вычислительной геометрии.

Джонатан Шевчук

Недвижимость треугольника | Типы и формулы с примерами

- Классы
  Класс 1–3
  Класс 4–5
  Класс 6–10
  Класс 11–12
- КОНКУРЕНТНЫЙ ЭКЗАМЕН
  BNAT
  BNAT Книги NCERT
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 11
  Класс NCERT
  Aggarwal
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10 90 005
  Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  RD Sharma
  RD Sharma Class 6 Solutions
  Решения RD Sharma Class 7
  Решения RD Sharma Class 8
  Решения RD Sharma Class 9
  Решения RD Sharma Class 10
  Решения RD Sharma Class 11
  Решения RD Sharma Class 12
  PHYSICS
  Механика
  Оптика
  Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Pythagoras
  000 9000 9000 Числа
  Взаимосвязи и функции
  Последовательность и серия
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Разделение фракций
  FORMULAS
  Maths Formulas
  Algebra Formulas
  Trigonometry Formulas
  Geometry Formulas
  CALCULATORS
  Maths Calculators
  Physics Calculators
  Physics Calculators
  Physics Calculators
  для класса 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  CBSE Sa mple Papers for Class 12
  CBSE Предыдущий год Вопросник
  CBSE Предыдущий год Вопросник Class 10
  CBSE Предыдущий год Вопросник Class 12
  HC Verma Solutions
  HC Verma Solutions Class 11 Physics
  HC Verma Solutions Class 12 Physics
  Lakhmir Singh Solutions
  Lakhmir Singh Class 9 Solutions
  Lakhmir Singh Class 10 Solutions
  Lakhmir Singh Class 8 Solutions
  CBSE Notes
  CBSE Примечания 9
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  Примечания к редакции CBSE
  Примечания к редакции
  9001 9.
  Площадь равностороннего треугольника — формула, определение, вывод, примеры
  Классы
  Класс 1-3
  Класс 4-5
  Класс 6-10
  Класс 11-12
  КОНКУРЕНТНЫЙ ЭКЗАМЕН
  BNAT 000 NC
  BNAT 000 Книги
  Книги NCERT для класса 5
  Книги NCERT для класса 6
  Книги NCERT для класса 7
  Книги NCERT для класса 8
  Книги NCERT для класса 9
  Книги NCERT для класса 10
  Книги NCERT для класса 11
  Книги NCERT для класса 12
  NCERT Exemplar
  NCERT Exemplar Class 8
  NCERT Exemplar Class 9
  NCERT Exemplar Class 10
  NCERT Exemplar Class 11
  NCERT Exemplar Class 11
  NCERT 9000 9000
  NCERT
  Решения RS Aggarwal, класс 12
  Решения RS Aggarwal, класс 11
  Решения RS Aggarwal, класс 10
  90 003 Решения RS Aggarwal класса 9
  Решения RS Aggarwal класса 8
  Решения RS Aggarwal класса 7
  Решения RS Aggarwal класса 6
  Решения RD Sharma
  RD Sharma Class 6 Решения
  Решения RD Sharma
  Решения RD Sharma класса 8
  Решения RD Sharma класса 9
  Решения RD Sharma класса 10
  Решения RD Sharma класса 11
  Решения RD Sharma класса 12
  PHYSICS
  Механика
  Оптика
  Термодинамика Электромагнетизм
  ХИМИЯ
  Органическая химия
  Неорганическая химия
  Периодическая таблица
  MATHS
  Теорема Пифагора
  000
  00030003000300030004
  Простые числа
  Взаимосвязи и функции
  Последовательности и серии
  Таблицы умножения
  Детерминанты и матрицы
  Прибыль и убыток
  Полиномиальные уравнения
  Деление фракций
  000
  000
  000
  000
  000 BIOG3000
  FORMULAS
  Математические формулы
  Алгебраные формулы
  Тригонометрические формулы
  Геометрические формулы
  КАЛЬКУЛЯТОРЫ
  Математические калькуляторы
  000 PBS4000
  000
  000 Физические калькуляторы
  000
  000
  000 PBS4000
  000
  000 Калькуляторы для химии
  Класс 6
  Образцы бумаги CBSE для класса 7
  Образцы бумаги CBSE для класса 8
  Образцы бумаги CBSE для класса 9
  Образцы бумаги CBSE для класса 10
  Образцы бумаги CBSE для класса 11
  Образцы бумаги CBSE чел. для класса 12
  CBSE, вопросник за предыдущий год
  CBSE, вопросник за предыдущий год, класс 10
  CBSE, вопросник за предыдущий год, класс 12
  HC Verma Solutions
  HC Verma Solutions, класс 11, физика
  Решения HC Verma, класс 12, физика
  Решения Лахмира Сингха
  Решения Лакмира Сингха, класс 9
  Решения Лакмира Сингха, класс 10
  Решения Лакмира Сингха, класс 8
  Примечания CBSE
  , класс
  CBSE Notes
  Примечания CBSE класса 7
  Примечания CBSE класса 8
  Примечания CBSE класса 9
  Примечания CBSE класса 10
  Примечания CBSE класса 11
  Примечания CBSE класса 12
  Примечания к редакции CBSE
  Примечания к редакции
  CBSE Class
  Примечания к редакции класса 10 CBSE
  Примечания к редакции класса 11 CBSE 9000 4
  Примечания к редакции класса 12 CBSE
  Дополнительные вопросы CBSE
  Дополнительные вопросы по математике класса 8 CBSE
  Дополнительные вопросы по науке 8 класса CBSE
  Дополнительные вопросы по математике класса 9 CBSE
  Дополнительные вопросы по науке класса 9 CBSE
  Дополнительные вопросы по математике для класса 10
  .