Развертки геометрических фигур для склеивания: Развёртки геометрических фигур
Развёртки геометрических фигур
Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.





Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

Довольно интересная фигура – ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

Развёртки геометрических объёмных тел
На плотной бумаге начертите подобную развёртку, вырежьте, аккуратно склейте.

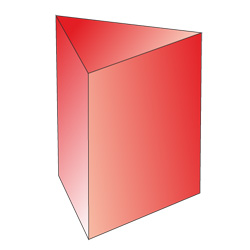
Треугольная призма
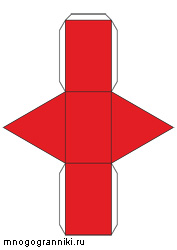
Четырёхугольная призма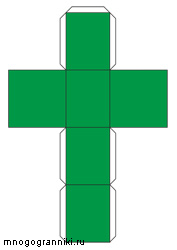

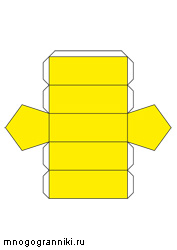
Пятиугольная призма
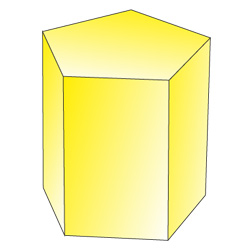
Шестиугольная призма 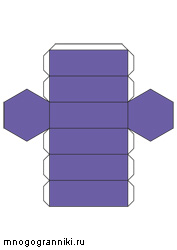
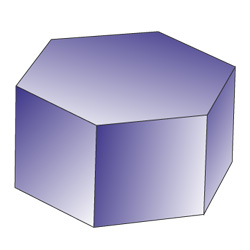
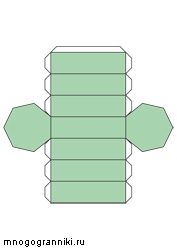
Семиугольная призма
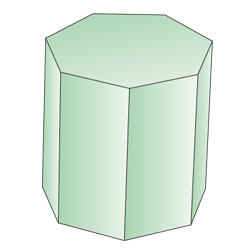
Восьмиугольная призма
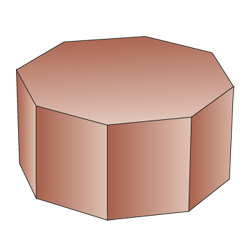
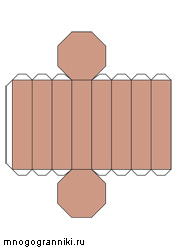
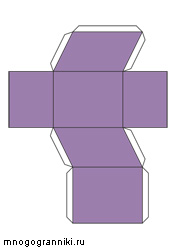
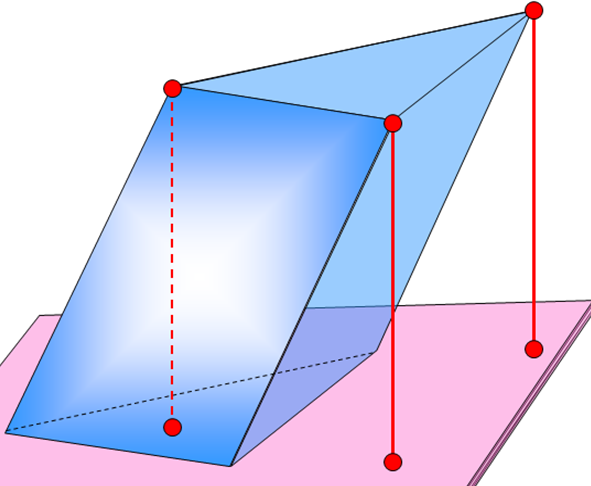
Наклонный параллелепипед
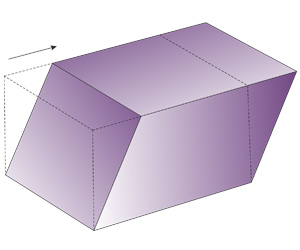
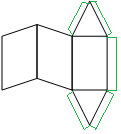
Наклонная треугольная призма
Цилиндр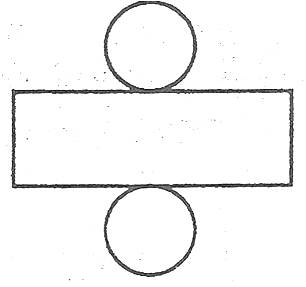

Конус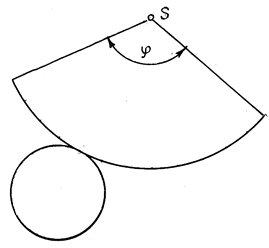

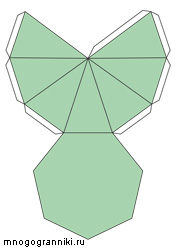
Пирамида
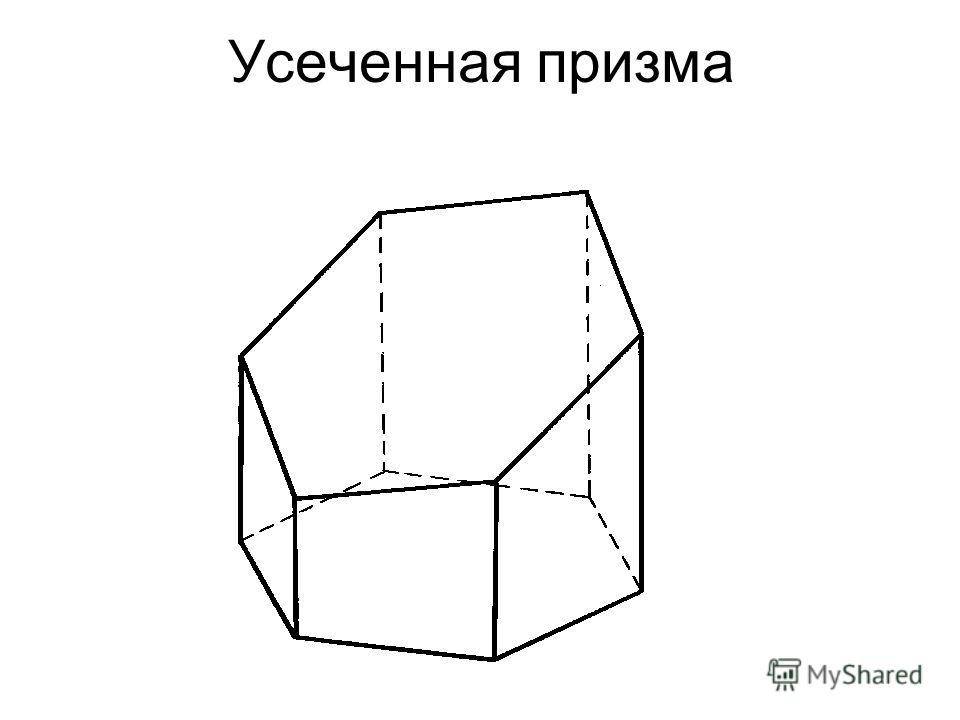
Усечённый цилиндр 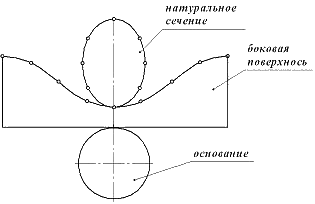

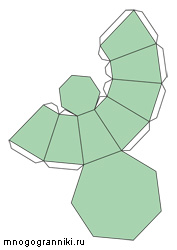
Усечённая пирамида
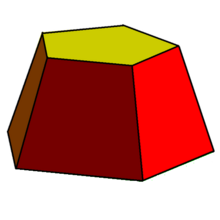
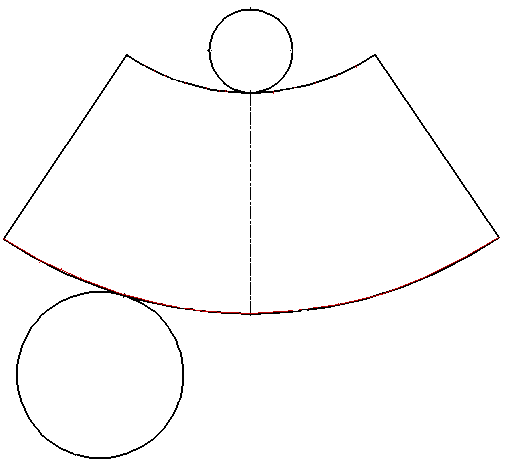
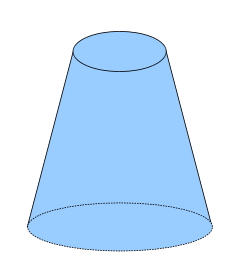
Усечённый конус
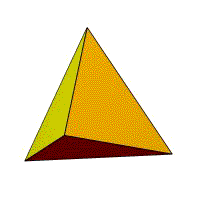
Тетраэдр
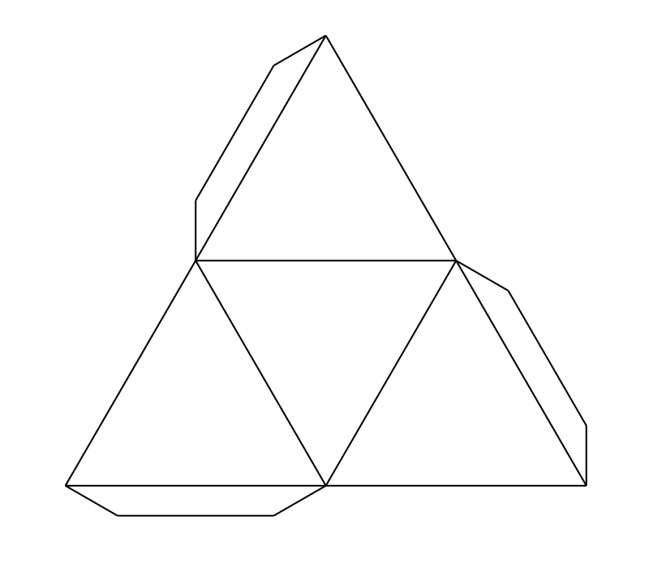
Октаэдр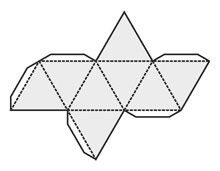

Икосаэдр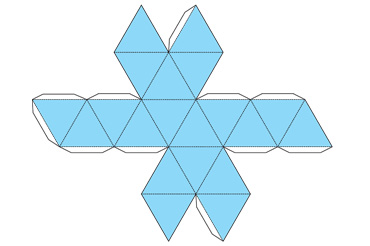

Додекаэдр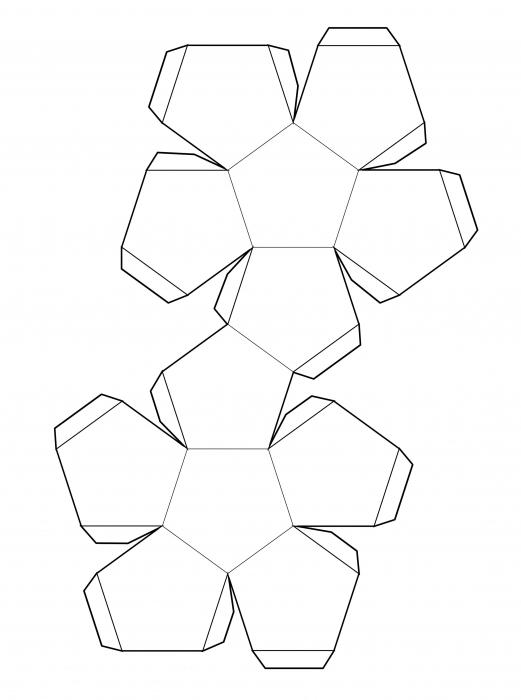
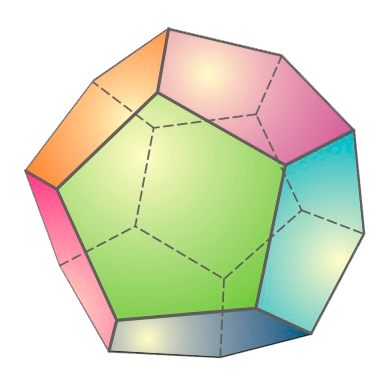
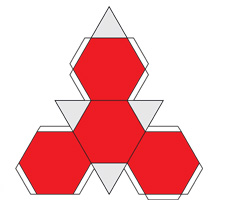
Усечённый тетраэдр

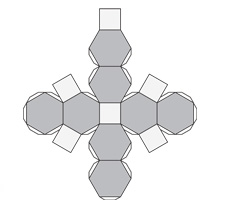
Усечённый октаэдр
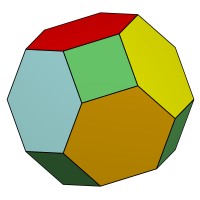
Усечённый куб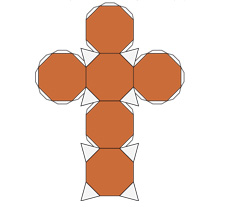

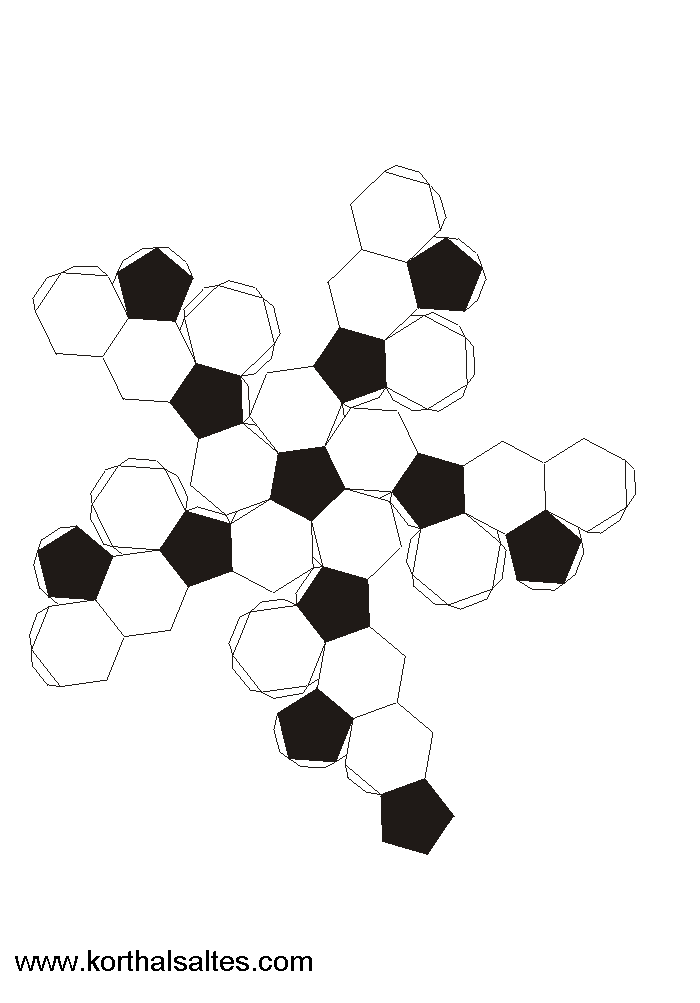
Усечённый икосаэдр

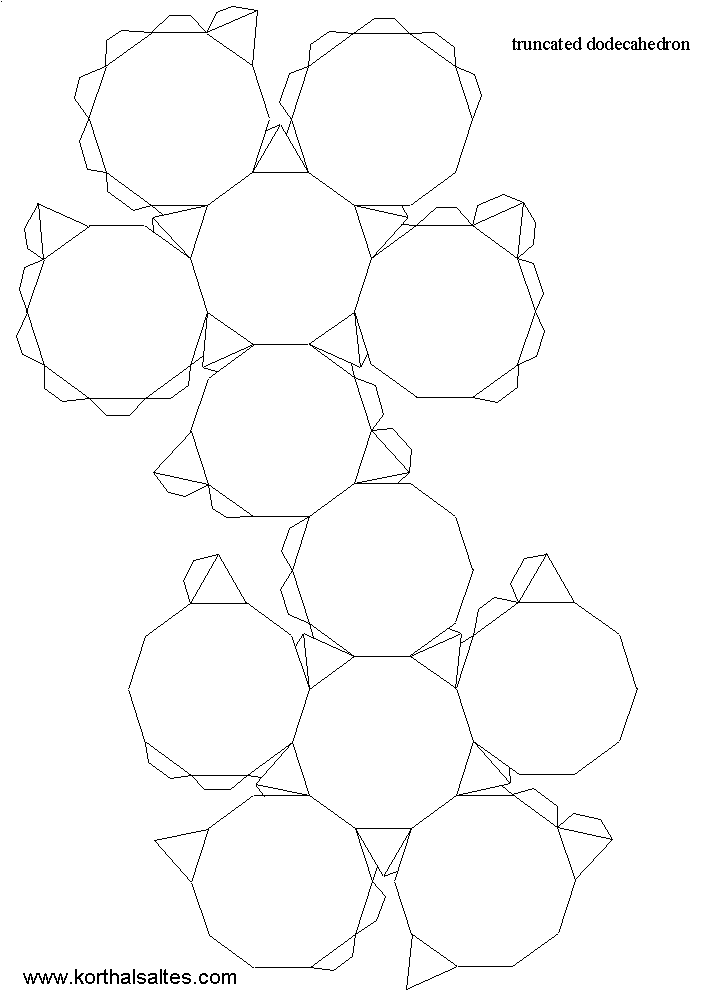
Усечённый додекаэдр
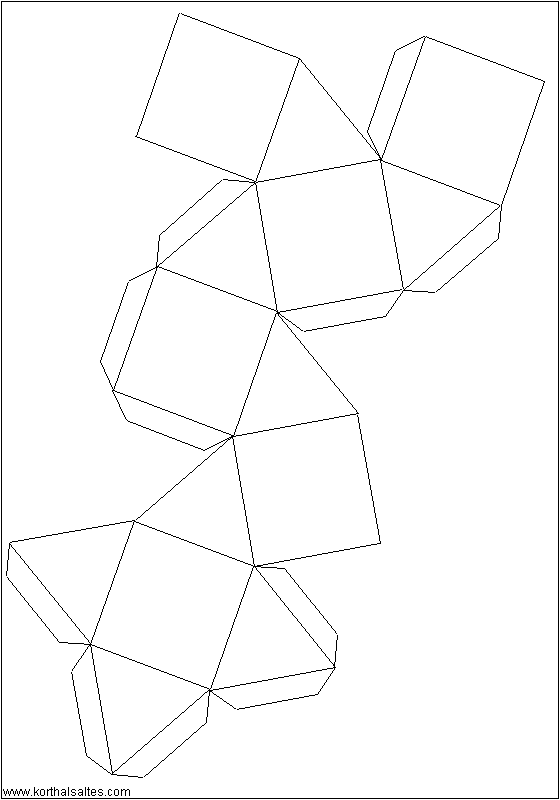
Кубооктаэдр
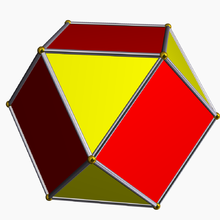
Икосододекаэдр
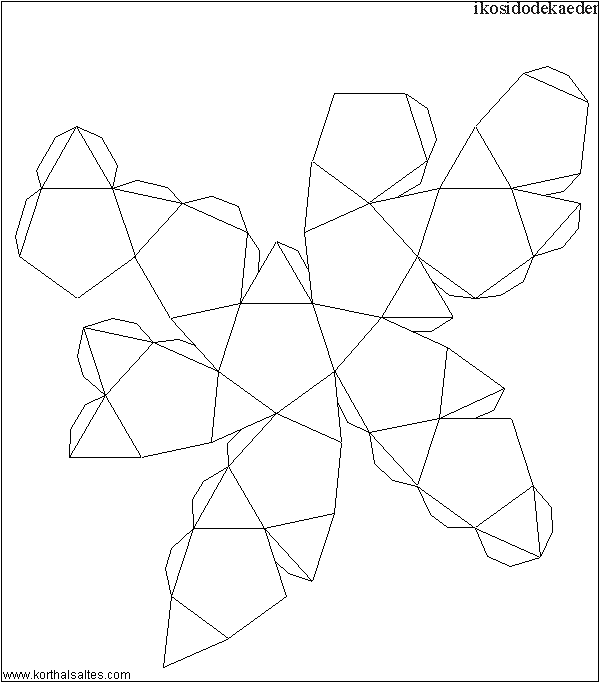

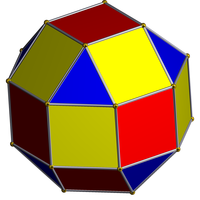
Ромбокубооктаэдр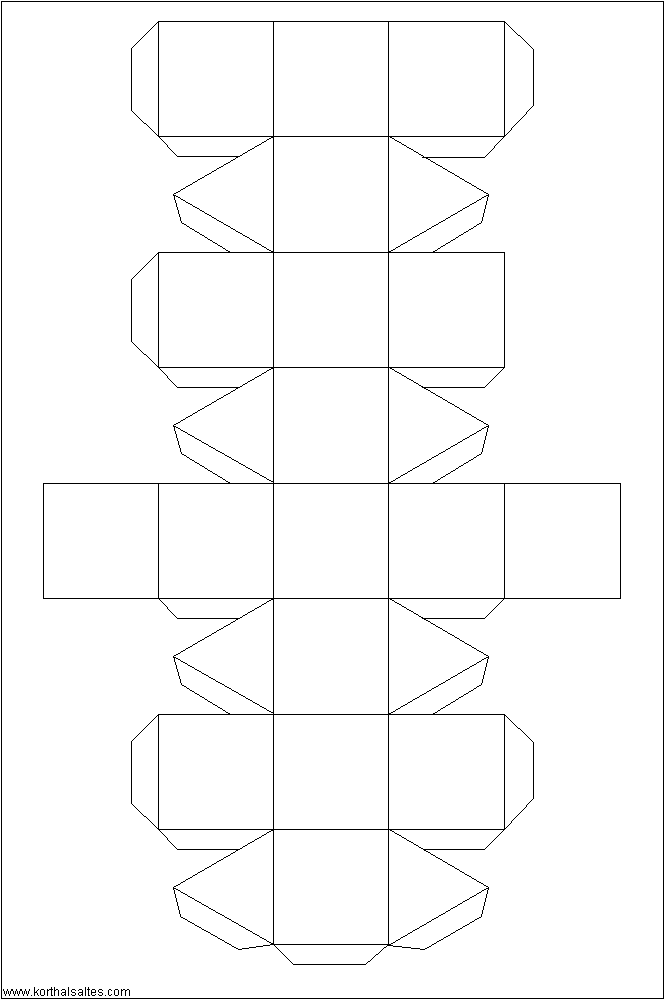
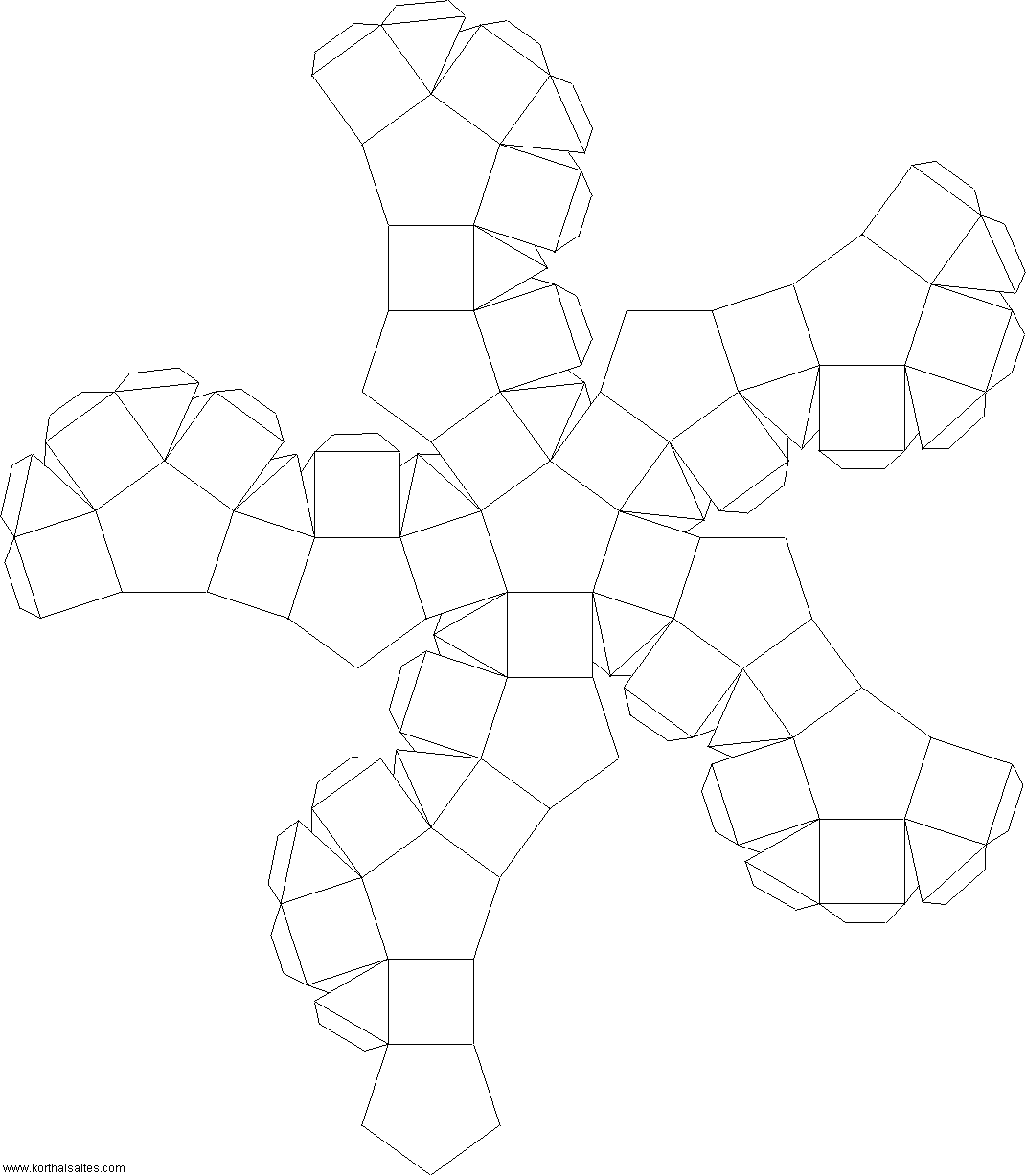
Ромбоикосододекаэдр

Ромбоусечённый 
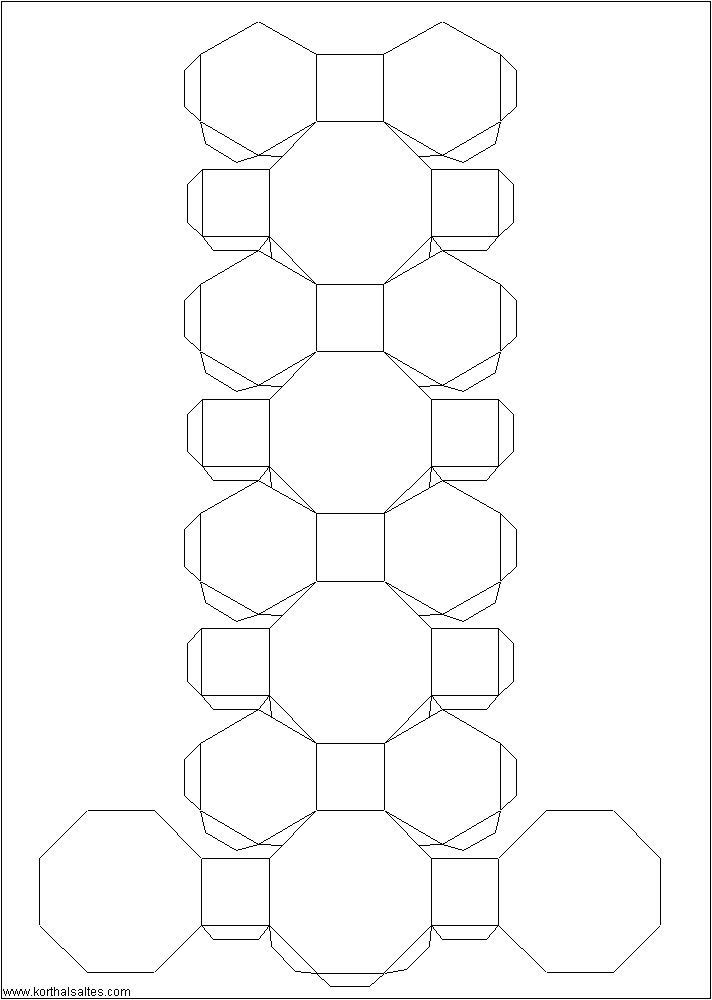
кубооктаэдр
Ромбоусечённый 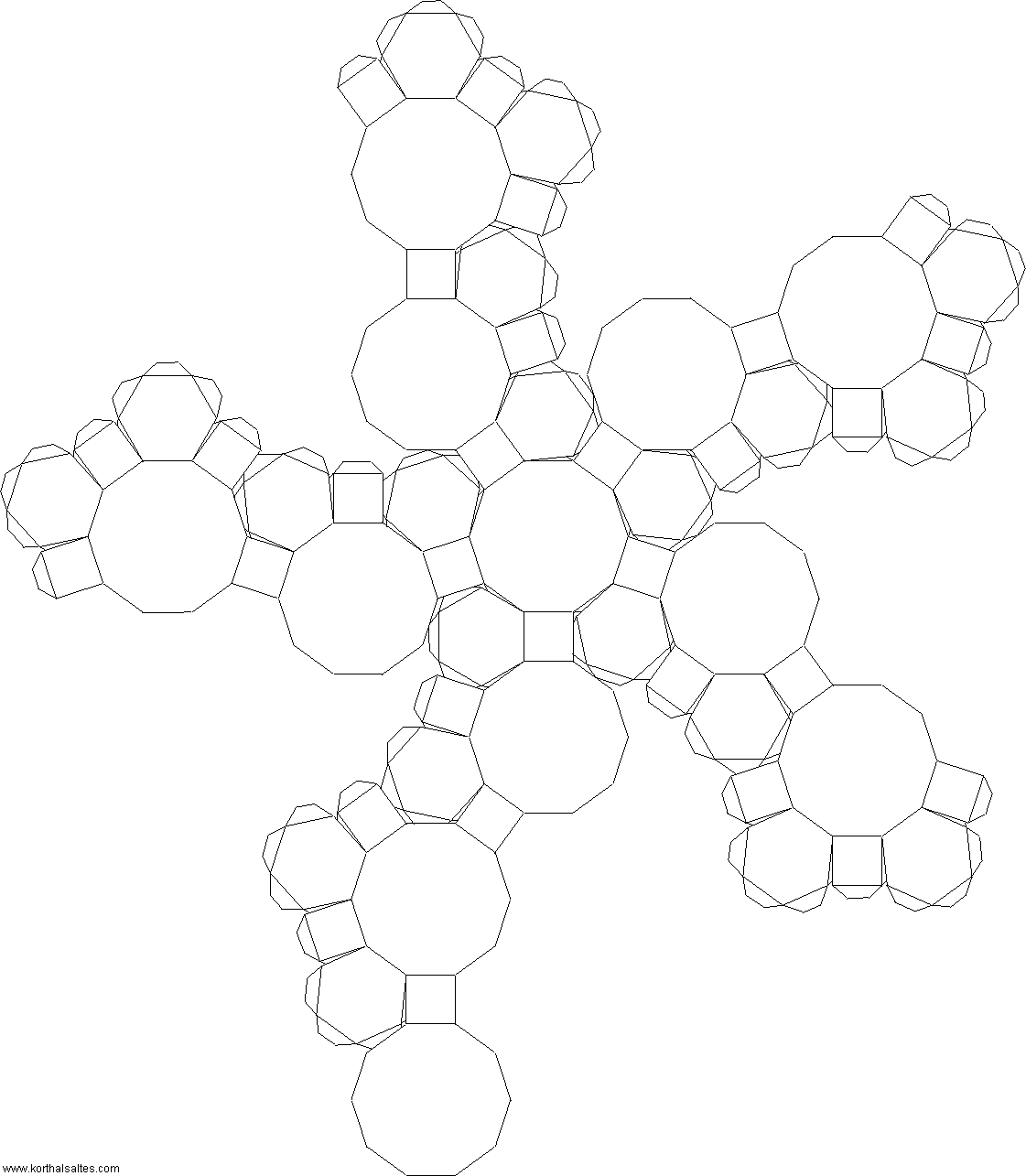
икосододекаэдр

Курносый куб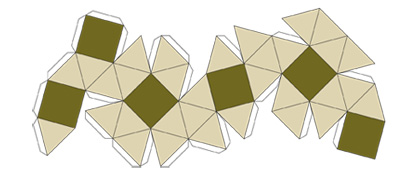

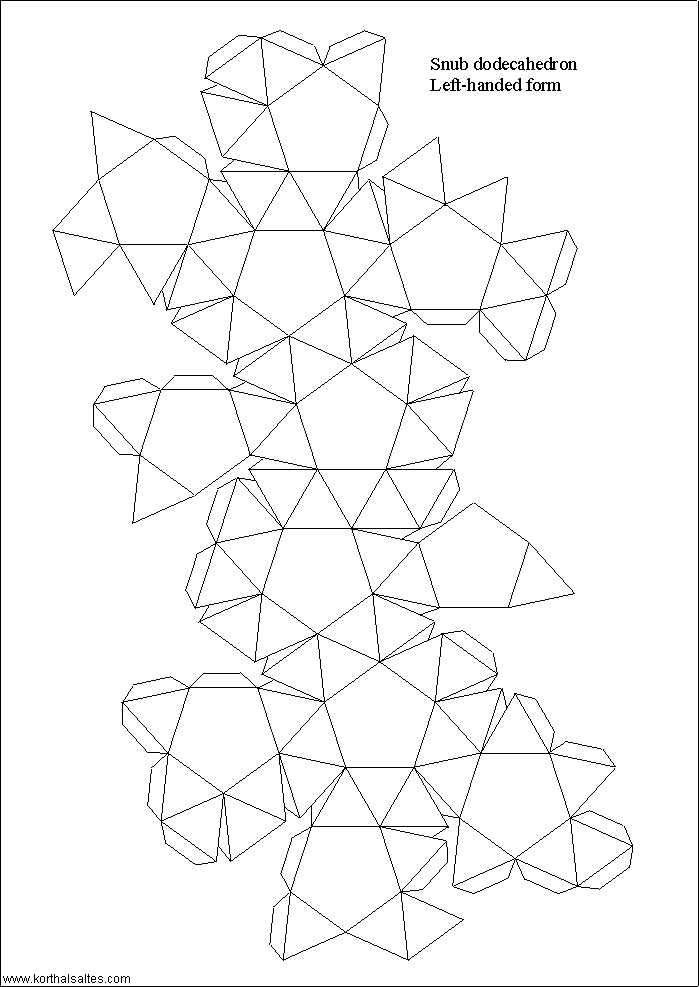
Курносый додекаэдр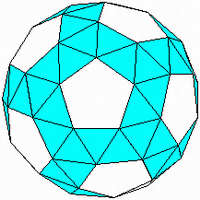
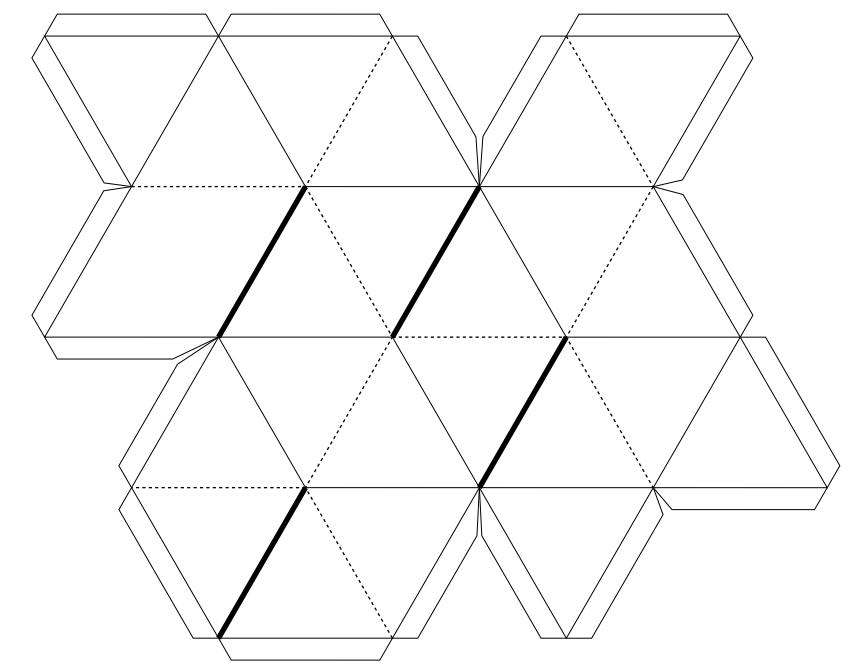
Звёздчатый октаэдр

Малый звёздчатый 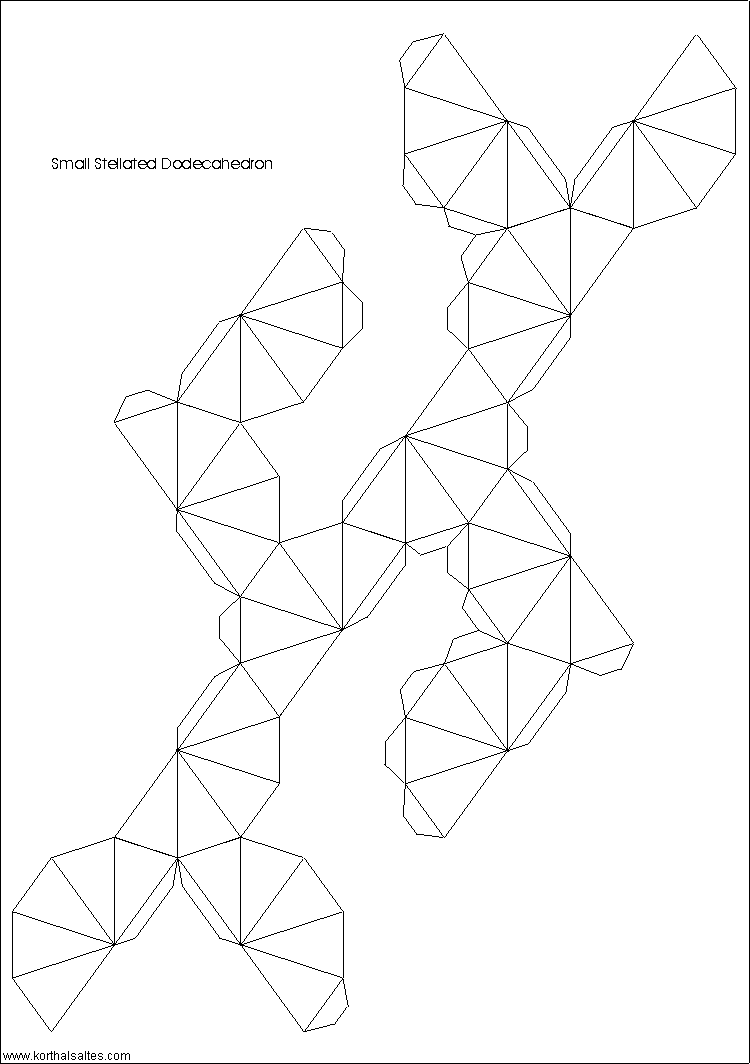
додекаэдр

Большой додекаэдр
Состоит из 4-х деталей, причем детали под номерами № 3 и 4 — по одной штуке,
а № 1 и 2 — по две штуке
Развертка состоит из прямоугольных треугольников, включает в себя еще и клапаны.
Согнуть развертку по всем необходимым линиям.
на схеме треугольнички, составляющие звездочку, выделены «крестиками»

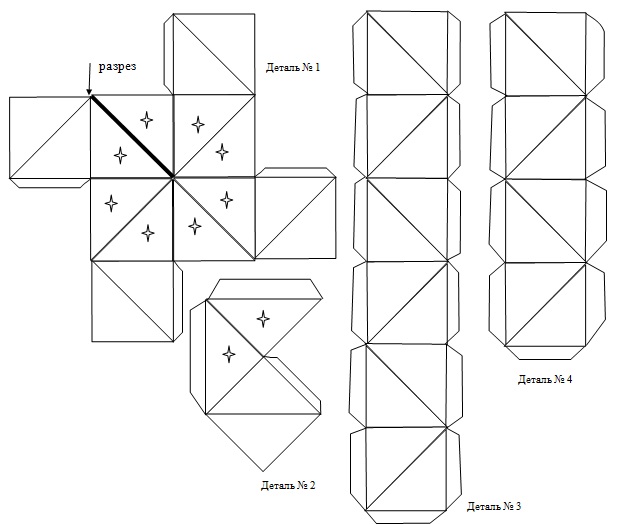
Большой звёздчатый додекаэдр:
клеим пирамидки соответствующего размера на додекаэдр

Соединение пяти октаедров
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.
Объемные геометрические фигуры из бумаги — Вырезаем и клеим:
Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Скачать геометрические фигуры из бумаги — развертки для вырезания вы можете во вложениях внизу страницы
Лист 1

Лист 2

Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: «Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.
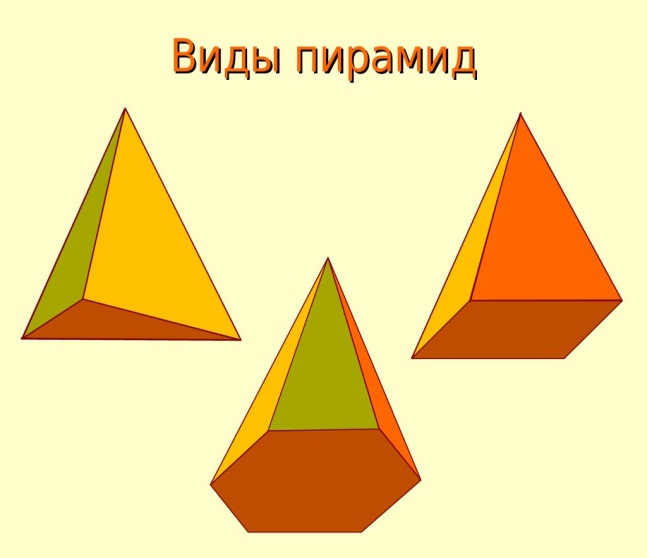
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:

Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)

Что такое куб:

Что такое конус и цилиндр. На что они похожи:

Можете также скачать эти обучающие картинки во вложениях.
Плоские геометрические фигуры из бумаги — Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
«Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.
Карточка 1

Карточка 2

Карточка 3

Карточка 4

Карточка 5

Карточка 6

Геометрические фигуры для вырезания:

Также вам будут полезны и другие материалы по изучению геометрических фигур:
 Рисунки из геометрических фигур — Задания в картинках и раскраски
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
 Геометрические фигуры — Раскраска для дошкольников
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
 Плоские геометрические фигуры — Обведи и дорисуй
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
 Найди формы геометрических фигур в картинках
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
 Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
 Свойства геометрических фигур для дошкольников
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
 Счет геометрических фигур — Картинки с заданиями
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
 Чертежи геометрических тел — Задание для детей
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
 Счет до 10 для детей дошкольного возраста
Счет до 10 для детей дошкольного возраста
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
 Игра «Что лишнее? — Геометрические формы»
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Геометрические фигуры схемы
Как сделать объемные геометрические фигуры из бумаги, развертки для склеивания: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника
Любому ребенку нравится делать яркие и объемные поделки. Творчество можно объединить с изучением математики и склеить вместе с детьми геометрические фигуры. Ребенок с интересом проведет время, а дополнительно постигнет основы точной науки. Ниже представлено, как начертить карандашом и сделать объемные геометрические фигуры из бумаги, также приведены их правильные названия.
Как сделать объемные геометрические фигуры
Дети познают мир в процессе игры и творчества. Трехмерные фигуры, выполненные своими руками, помогут познакомиться с удивительной наукой — геометрией.
Примеры трафаретов и шаблонов можно скачать из Интернета и распечатать. Затем все фигуры вырезают и склеивают. Дети старшего возраста могут самостоятельно нарисовать развертку нужной фигуры, малышам помогают родители,.
Геометрические объекты делают из бумаги (белой или цветной), картона. Из последнего материала они получаются плотными и прочными.
к оглавлению ^
Из бумаги
к оглавлению ^
Из картона
к оглавлению ^
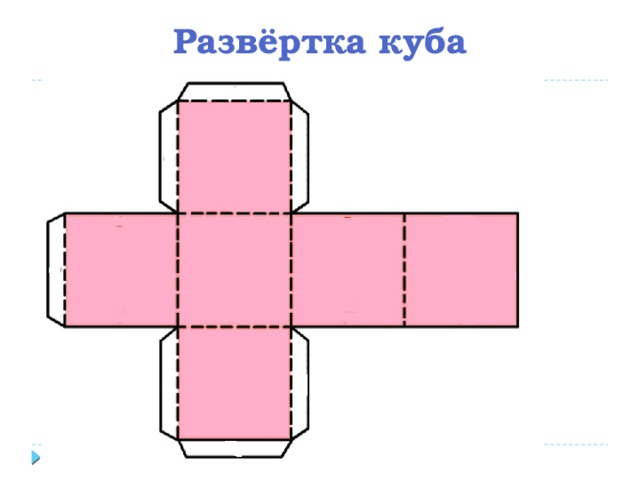
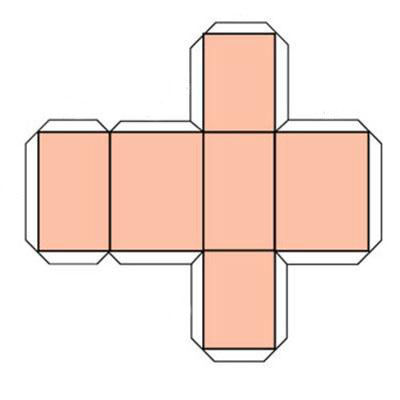
Развертки куба
к оглавлению ^
Треугольника
к оглавлению ^
Прямоугольника
к оглавлению ^
Цилиндра
к оглавлению ^
Ромба
к оглавлению ^
к оглавлению ^
Схемы для вырезания
Ученикам 1–2 класса демонстрируют в школе простые геометрические фигуры и 3d: квадрат, кубик, прямоугольник. Их несложно вырезать и склеить. Шаблоны развивают мелкую моторику у детей и дают первые представления о геометрии.
Ученики средней школы, которые изучают черчение, делают сложные фигуры: бумажные шестигранники, фигуры из пятиугольников, цилиндры. Из бумаги для детей выполняют домики для кукол, мебель, оригами, замок для маленьких игрушек, маски на лицо (трехмерные называются полигональными).
к оглавлению ^
Конуса
к оглавлению ^
Пирамиды
к оглавлению ^
Шестигранника
к оглавлению ^
Макета с припусками
к оглавлению ^
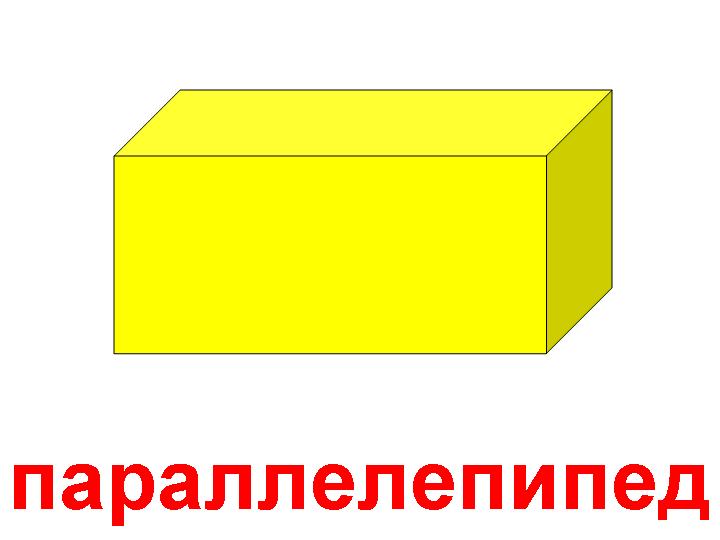
Параллелепипеда
к оглавлению ^
Трапеции
к оглавлению ^
Овала
к оглавлению ^
Шара
Выкройка шара состоит из 8 частей, 12, 16 или большего количества. Присутствуют и другие способы изображения мяча. Например, из 6 деталей или 4 широких клиньев.
Материал, из чего можно сделать плотный шар — картон или плотная бумага.
к оглавлению ^
Многогранника
к оглавлению ^
Параллелограмма
к оглавлению ^
Шаблоны для склеивания
Зачастую школьники задаются вопросом, что можно сделать из бумаги к урокам труда или на выставку. Работы ученика выделятся среди остальных, если это будут сложные трехмерные предметы, рельефные геометрические фигуры, платоновы тела, шаблоны кристаллов и минералов.
Если следовать инструкции, то ученик 5–6 класса сможет без помощи родителей сделать точный додекаэдр или тетраэдр.
Иногда в школе задают логические задания, как из квадрата сделать круг или шестиугольник. Для этого определить центр квадрата, согнув его по диагонали. Точка пересечения прямых — центр квадрата и будущего круга. Исходя из этого, можно начертить круг.
к оглавлению ^
Сложных фигур
к оглавлению ^
3d
Инфоурок
›
Другое
›Презентации›Презентация к уроку черчения «Развертки геометрических тел» 8 класс
Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
«Чертежи и развертки простых геометрических тел» учитель черчения — Дудоладова Г.П.
2 слайд

Описание слайда:
Цели: Образовательная: познакомить учащихся с понятием «развёртка», с правильными многогранниками – с 5-ю Платоновыми фигурами, дочертить фигуры, развертки фигур. Развивающая: развивать пространственное видение предмета, умение вычерчивать развёртку и склеивать фигуру. Воспитывающая: воспитывать аккуратность при выполнении графической и практической работ, усидчивость, терпимость.
3 слайд

Описание слайда:
Задачи — закрепить понятие геометрические тела; — научить читать и строить чертежи и развертки простых геометрических тел; — способствовать самостоятельному изучению построению разверток геометрических тел; — развивать пространственные представления и мышление, умение работать с информационными источниками; — воспитывать чувство времени, аккуратность, усидчивость.
4 слайд

Описание слайда:
Тип урока: урок изучения нового материала Материальное обеспечение: модели геометрических тел, карточки — задания, учебники, чертежные принадлежности, чертежная бумага.
5 слайд
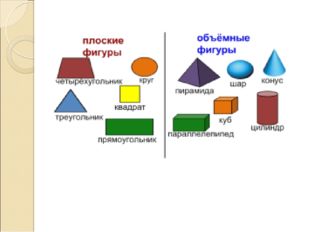
Описание слайда:
6 слайд
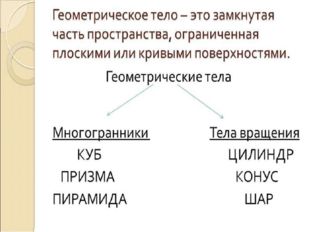
Описание слайда:
7 слайд
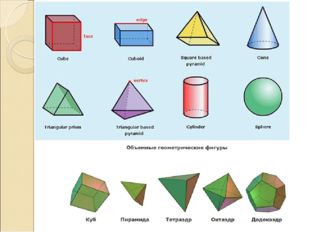
Описание слайда:
8 слайд

Описание слайда:
Моделирование из бумаги макетов геометрических тел
9 слайд

Описание слайда:
РАЗВЕРТКА С развёртками поверхностей мы часто встречаемся в обыденной жизни, на производстве, в строительстве. Чтобы изготовить упаковку для сока, конфет, духов, праздничную коробочку или кулёк и т.п., надо уметь строить развёртки поверхностей геометрических тел.
10 слайд

Описание слайда:
«Развёртка» — представляет собой плоский многоугольник, состоящий из меньших многоугольников – граней исходного многогранника.
11 слайд
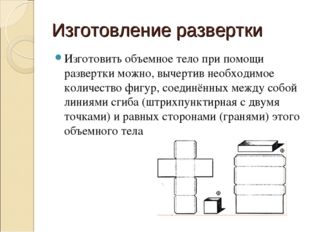
Описание слайда:
Изготовление развертки Изготовить объемное тело при помощи развертки можно, вычертив необходимое количество фигур, соединённых между собой линиями сгиба (штрихпунктирная с двумя точками) и равных сторонами (гранями) этого объемного тела
12 слайд

Описание слайда:
Инструменты и материалы, необходимые для выполнения макетов геометрических тел
13 слайд
Описание слайда:
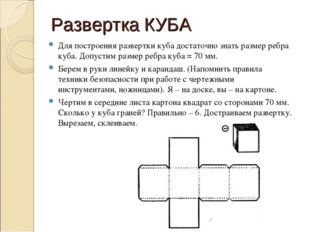
Развертка КУБА Для построения развертки куба достаточно знать размер ребра куба. Допустим размер ребра куба = 70 мм. Берем в руки линейку и карандаш. (Напомнить правила техники безопасности при работе с чертежными инструментами, ножницами). Я – на доске, вы – на картоне. Чертим в середине листа картона квадрат со сторонами 70 мм. Сколько у куба граней? Правильно – 6. Достраиваем развертку. Вырезаем, склеиваем.
14 слайд
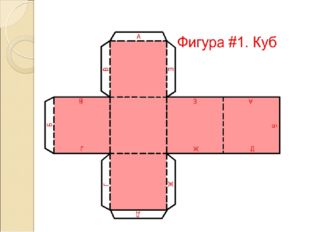
Описание слайда:
15 слайд
Описание слайда:
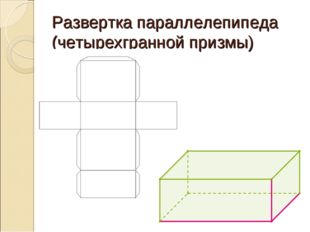
Развертка параллелепипеда (четырехгранной призмы)
16 слайд
Описание слайда:
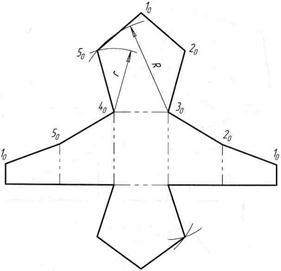
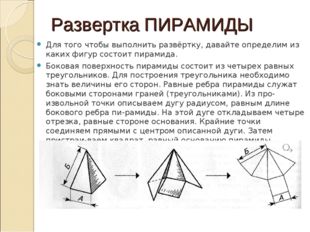
Развертка ПИРАМИДЫ Для того чтобы выполнить развёртку, давайте определим из каких фигур состоит пирамида. Боковая поверхность пирамиды состоит из четырех равных треугольников. Для построения треугольника необходимо знать величины его сторон. Равные ребра пирамиды служат боковыми сторонами граней (треугольниками). Из произвольной точки описываем дугу радиусом, равным длине бокового ребра пирамиды. На этой дуге откладываем четыре отрезка, равные стороне основания. Крайние точки соединяем прямыми с центром описанной дуги. Затем пристраиваем квадрат, равный основанию пирамиды.
17 слайд
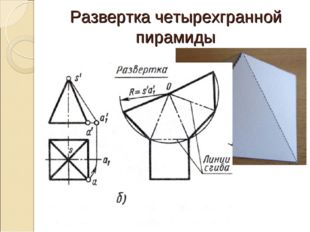
Описание слайда:
Развертка четырехгранной пирамиды
18 слайд
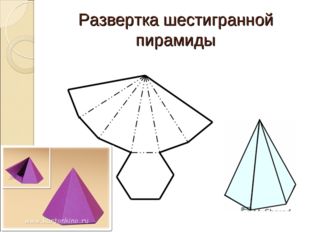
Описание слайда:
Развертка шестигранной пирамиды
19 слайд
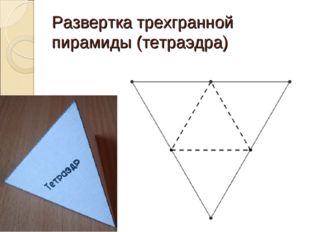
Описание слайда:
Развертка трехгранной пирамиды (тетраэдра)
20 слайд

Описание слайда:
21 слайд

Описание слайда:
22 слайд
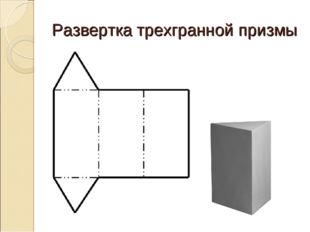
Описание слайда:
Развертка трехгранной призмы
23 слайд
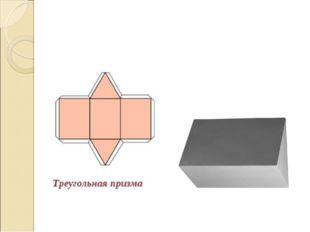
Описание слайда:
24 слайд
Описание слайда:
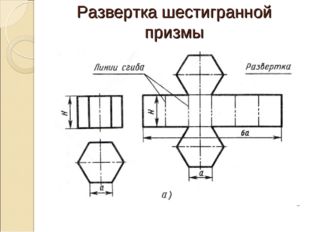
Развертка шестигранной призмы
25 слайд
Описание слайда:
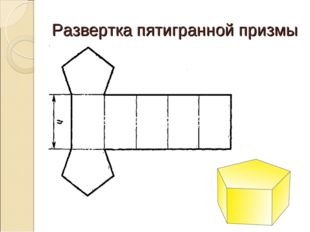
Развертка пятигранной призмы
26 слайд

Описание слайда:
27 слайд
Описание слайда:
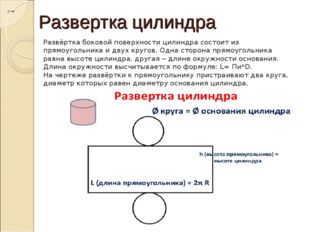
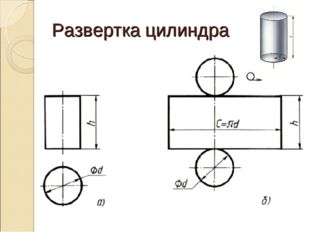
Развертка цилиндра Развёртка боковой поверхности цилиндра состоит из прямоугольника и двух кругов. Одна сторона прямоугольника равна высоте цилиндра, другая – длине окружности основания. Длина окружности высчитывается по формуле: L= Пи*D. На чертеже развёртки к прямоугольнику пристраивают два круга, диаметр которых равен диаметру основания цилиндра.
28 слайд
Описание слайда:
Развертка цилиндра
29 слайд

Описание слайда:
30 слайд
Описание слайда:
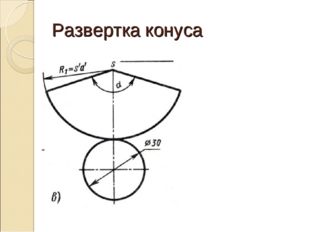
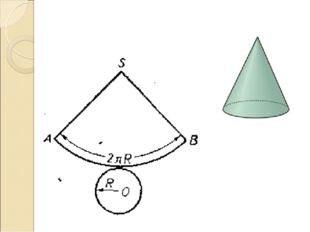
Развертка конуса
31 слайд
Описание слайда:
32 слайд
Описание слайда:
33 слайд
Описание слайда:
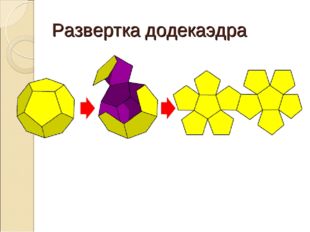
Развертка додекаэдра
34 слайд
Описание слайда:
35 слайд

Описание слайда:
36 слайд

Описание слайда:
37 слайд

Описание слайда:
38 слайд

Описание слайда:
39 слайд

Описание слайда:
40 слайд

Описание слайда:
Домашнее задание Изготовить модель геометрического тела высотой не менее 20 см
41 слайд
Описание слайда:

Курс повышения квалификации

Курс профессиональной переподготовки
Педагог-библиотекарь

Курс профессиональной переподготовки
Библиотекарь
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию:
Все категорииАлгебраАнглийский языкАстрономияБиологияВнеурочная деятельностьВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс:
Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник:
Все учебники
Выберите тему:
Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала:
ДБ-395822
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарий
Развертки тел вращения — Mnogogranniki.ru

Что будет, если плоскую геометрическую фигуру, например прямоугольник, начать быстро вращать относительно одной из его сторон?
Одним лишь вращением мы можем создать новое геометрическое тело в пространстве.
Боковые поверхности цилиндра образуются за счет сторон вращающегося прямоугольника.
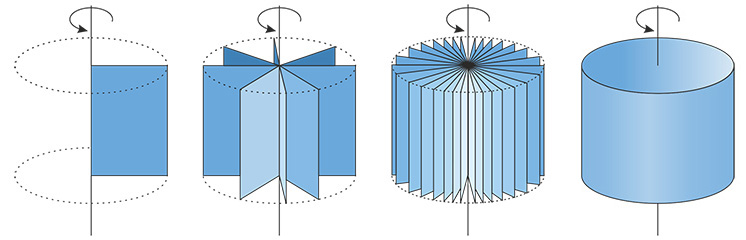
Официальное определение для таких геометрических тел, звучит следующим образом:
Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.
И здесь важно то, что плоская геометрическая фигура может быть совершенно произвольной формы.
Например, кривая, которая при вращении будет образовывать вазу или лампочку. Такие инструменты создания тел вращения очень популярны у тех, кто работает в программах 3D-проектирования.

Но с математической точки зрения, для нас, прежде всего, интересны следующие геометрические тела вращения:
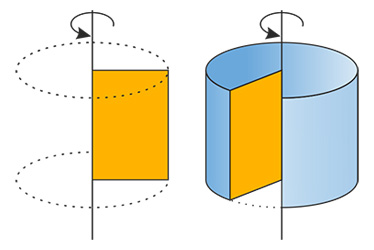
Цилиндр — образован прямоугольником, вращающимся вокруг одной из сторон.
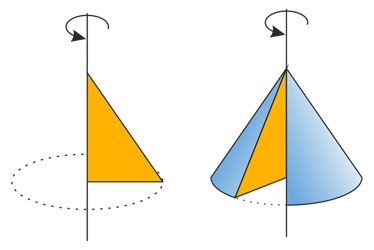
Конус — образован прямоугольным треугольником, вращающимся вокруг одного из катетов.
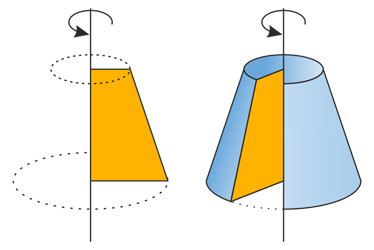
Усечённый конус — часть конуса, расположенная между его основанием и секущей плоскостью, параллельной основанию.
Образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции.
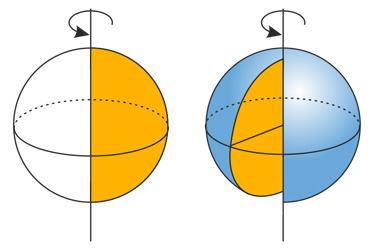
Шар — образован полукругом, вращающимся вокруг диаметра разреза.
При вращении контуров фигур возникает поверхность вращения (например, сфера, образованная окружностью), в то время как при вращении заполненных контуров возникают тела (как шар, образованный кругом).
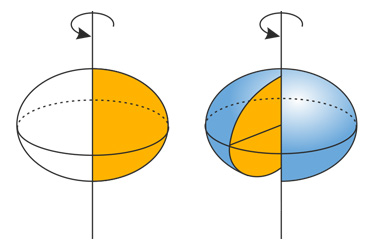
Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
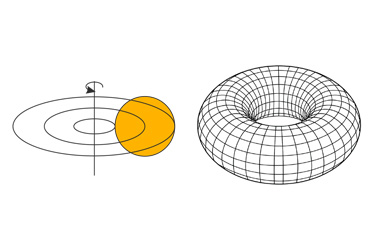
Тор — образован окружностью, вращающейся вокруг прямой, не пересекающей его.
В обычном понимании тор — это «бублик».
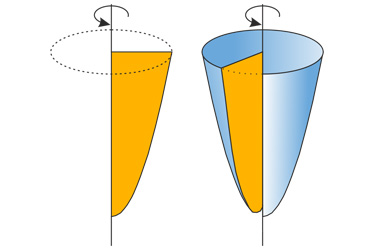
Параболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком параболы. Отсюда и название параб-о-лоид.
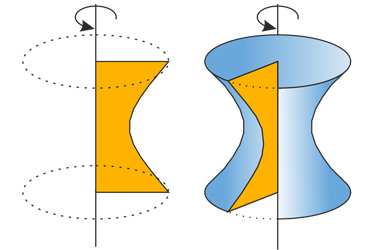
Гиперболоид — это поверхность, которая образуется в результате вращения вокруг оси кривой образованной графиком гиперболы. Соответственно название гиперб-о-лоид.
Как сделать цилиндр из бумаги?
Как сделать конус из бумаги?
Как сделать параболоид из бумаги?
Как сделать гиперболоид из бумаги?
Как сделать тор из бумаги?
Для сопоставимости размеров получающихся моделей тел вращения мы постарались собрать их на одной поверхности вместе с призмами из выпуска «Волшебные грани № 16».

Получился целый математический город из бумаги, умещающийся на столе!
Развертки фигур чертежи
Чертеж пересечения конуса и призмы с последующей разверткой.
Подробнее
Усеченная четырехугольная пирамида представлена в виде развертки и аксонометрии. Также на чертеже присутствуют элементы определения сечения в натуральную величину.
Подробнее
Чертеж развертки цилиндра по заданию чертился в САПР. На представленном чертеже присутствует фигура в трех проекциях, развертка с сечением в натуральную величину и аксонометрия с усеченной пирамидой.
Подробнее
Чертеж развертка усеченной пирамиды представляет собой комплексную задачу, состоящую из 4 задач: Определение сечения на трех видовых проекциях; Построение сечения в натуральную величину; Вычерчивание развертки усеченной пирамиды; Черчение изометрии данной […]
Подробнее
Чертеж развертки конуса был начерчен в результате пересечения с призмой. Точки линии пересечения определялись методом секущих плоскостей с соответствующим обозначением.
Подробнее
Необходимо было выполнить сечение призмы плоскостью. Для этого воспользуемся дополнительной линией. По заданию дана геометрическая фигура, необходимо было начертить секущую плоскость, проходящую по виду спереди и перенести полученный результат на […]
Подробнее
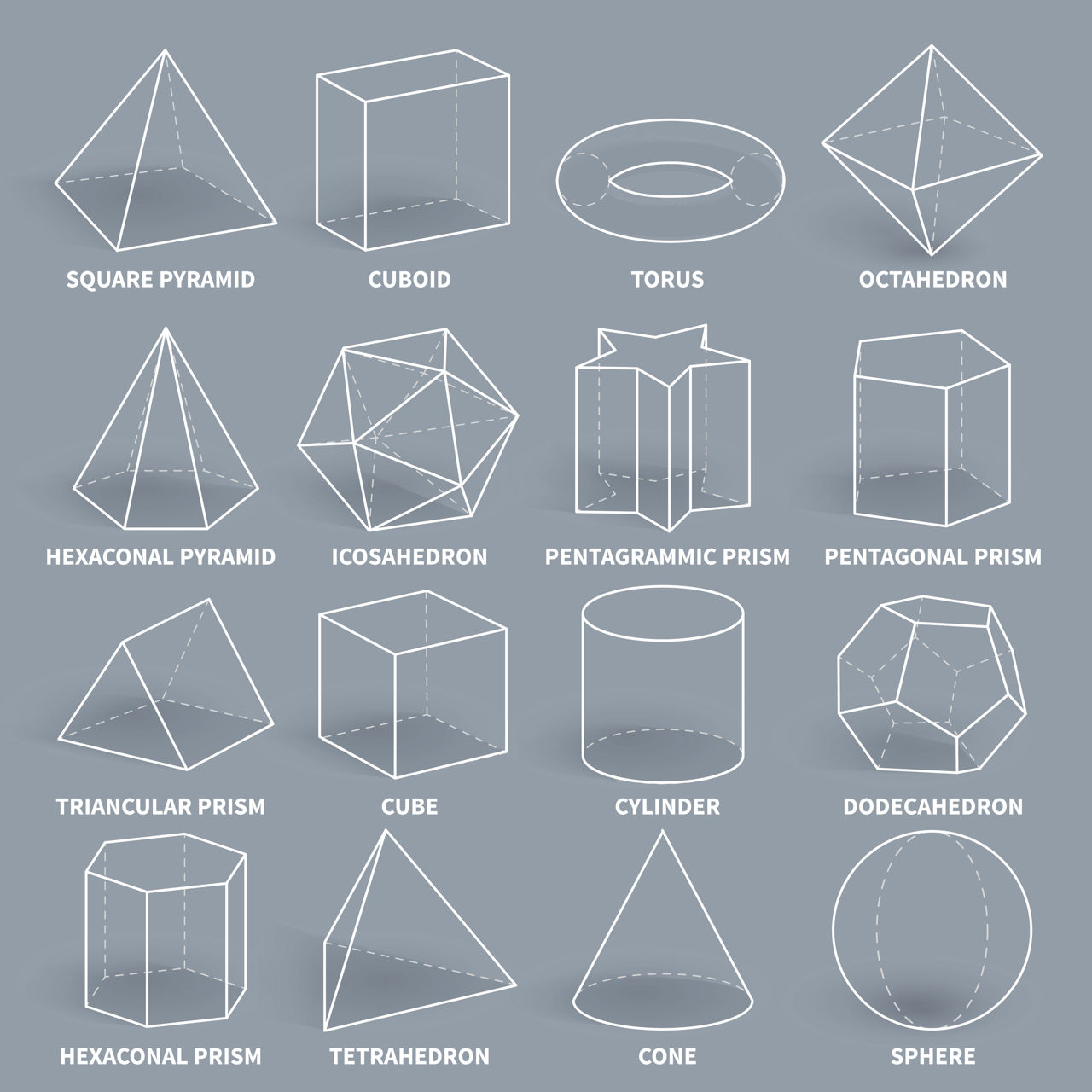
Мы сталкиваемся с различными типами объектов и материалов, которые в основном регулируются определенными геометрическими аспектами, которые делают их уникальными по-своему. Эта статья ScienceStruck предоставит вам подробную информацию о различных видах и названиях геометрических форм, а также их значения и изображения.
Быстрый Факт
Область геометрии и связанные с ней исследования форм и фигур, как сообщается, впервые появились в цивилизации реки Инд и в вавилонской цивилизации около 3000 г. до н.э.В нескольких сообщениях предполагается, что египтяне имели свою собственную версию теоремы Пифагора еще до того, как Пифагор сформулировал ее.
Хотите написать для нас? Ну, мы ищем хороших писателей, которые хотят распространять информацию. Свяжитесь с нами, и мы поговорим …
Давайте работать вместе!
Внешний вид или форма объекта или тела, которое остается стабильным или постоянным при определенных нормальных условиях, называется геометрической формой этого объекта. Проще говоря, геометрические фигуры характеризуются как внешние ориентации рассматриваемых объектов.Как параметры отличаются, так и типы формы. Если формы двух объектов одинаковы или похожи, говорят, что они совпадают друг с другом. Можно сказать, что любое известное тело или материалистическое существо во всей вселенной присутствует в форме геометрической формы.
В основном, существует два типа геометрических фигур: двумерные (2D) и трехмерные (3D). Первый может быть нарисован со ссылкой на оси X и Y, тогда как последний также включает в себя ось Z. 2D фигуры и фигуры в основном состоят из точек и соединительных линий, которые образуют фигуру.Они могут быть либо выпуклыми (обычного вида), либо вогнутыми (нерегулярными). На многих многоугольных двумерных фигурах выпуклые имеют углы менее 180 градусов, тогда как вогнутые фигуры имеют по меньшей мере один угол больше 180 градусов. Трехмерные фигуры являются более сложными и состоят в основном из вершин, ребер, граней и т. Д.
Следующие разделы помогут вам понять значение основных геометрических фигур вместе с их изображениями. Обратите внимание, что все указанные углы являются внутренними.
Различные типы геометрических фигур
Двумерные (2D) фигуры
Треугольники
Это тип многоугольника, который состоит из трех сторон с тремя вершинами. Сумма углов треугольника равна 180 градусам в любом типе. Обратитесь к разделу ниже для получения более подробной информации.
равнобедренный треугольник
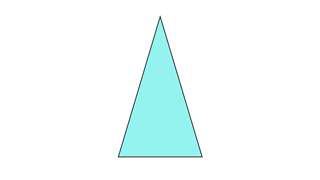
Две стороны имеют одинаковую длину, и два угла также равны.Линия симметрии присутствует.
Скален Треугольник
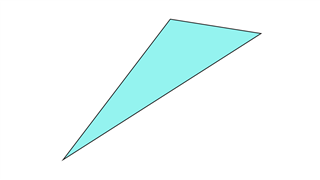
Длина всех сторон неодинакова, и все три угла имеют различные значения.
равносторонний треугольник
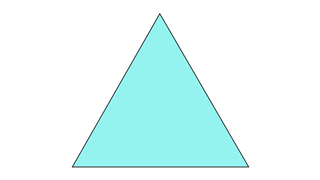
Все три стороны и углы равны. Линия симметрии присутствует.
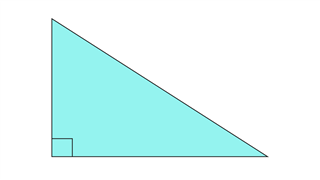
Прямоугольный треугольник
Хотите написать для нас? Ну, мы ищем хороших писателей, которые хотят распространять информацию.Свяжитесь с нами, и мы поговорим …
Давайте работать вместе!
Один из углов 90 градусов. Линия симметрии может присутствовать или не присутствовать.
Тупой Треугольник
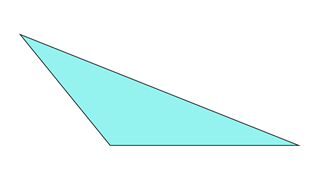
Один из углов больше 90 градусов. Линия симметрии может присутствовать или не присутствовать.
Острый треугольник
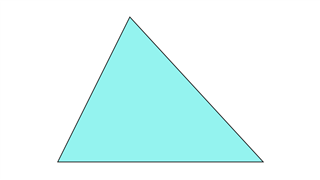
Все углы острые (менее 90 градусов).Линия симметрии может присутствовать или не присутствовать.
Четырехсторонние
Эти многоугольники состоят из четырех сторон, а сумма углов равна 360 градусам в любом типе. Обратитесь к разделу ниже для получения более подробной информации.
Прямоугольник

У них есть два набора противоположных сторон, которые равны, и все четыре угла 90 градусов. Две линии симметрии присутствуют.
Площадь

Все четыре угла равны 90 градусам вместе с четырьмя равными сторонами.Этот многоугольник имеет четыре линии симметрии.
Параллелограмм
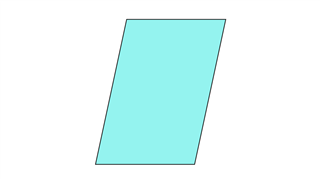
Они состоят из двух наборов противоположных линий, которые равны и параллельны. Противоположные углы также равны относительно любого значения. Линия симметрии может присутствовать.
Ромб
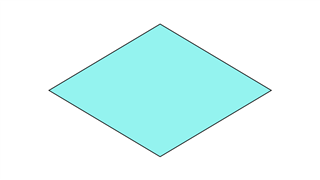
Все четыре стороны равны и параллельны, но равны только противоположные углы.Две линии симметрии присутствуют. Он тесно связан с квадратом и параллелограммом.
Трапеция
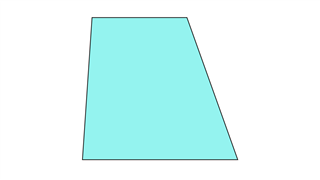
Один набор противоположных линий параллелен, а другой набор непараллелен. Линия симметрии может присутствовать. Это называется Трапеция в Великобритании.
Трапеция
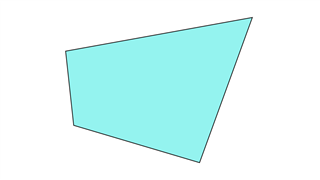
Все четыре стороны неравны и не параллельны, а линия симметрии отсутствует.Это называется трапеция в Великобритании.
Воздушный змей
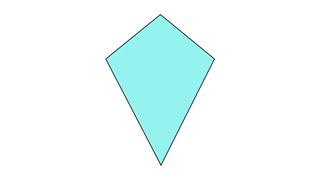
Два набора смежных сторон равны, и два противоположных угла также имеют равные значения. Линия симметрии присутствует.
Нерегулярный Четырехсторонний
Он имеет четыре неравные стороны, и его внешний вид является вогнутым, то есть, по меньшей мере, один угол больше 180 градусов.
полигонов
Фигуры, состоящие из трех или более трех сторон, называются полигонами. Углы такого типа геометрических фигур могут составлять более 360 градусов. Как правильные, так и неправильные типы полигонов приведены ниже.
Примечание : Хотя типы треугольников и четырехугольников включены в Polygons, как они были описаны выше, они не перечислены в следующем разделе.
Пентагон
Он состоит из пяти равных сторон, а сумма углов равна 540 градусам.Пять линий симметрии присутствуют.
Шестигранник
Он состоит из шести равных сторон, а сумма углов равна 720 градусам. Шесть линий симметрии присутствуют.
семиугольник
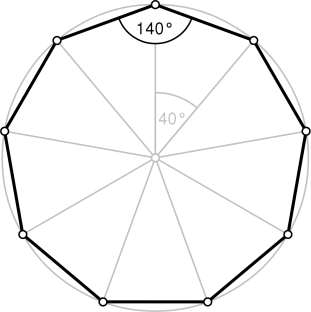
Он состоит из семи равных сторон, а сумма углов равна 900 градусов. Семь линий симметрии присутствуют.
Октагон
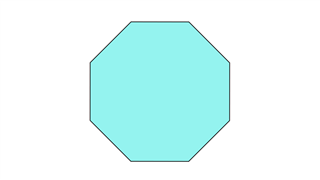
Он состоит из восьми равных сторон, а сумма углов равна 1080 градусов. Восемь линий симметрии присутствуют.
Нонагон
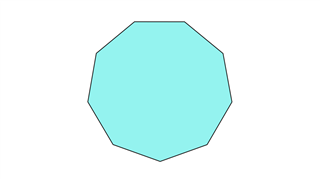
Он состоит из девяти равных сторон, а сумма углов равна 1260 градусам. Девять линий симметрии присутствуют.
Декагон
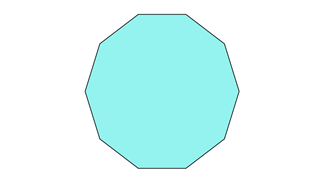
Он состоит из десяти равных сторон, а сумма углов равна 1440 градусам.Десять линий симметрии присутствуют.
Додекагон
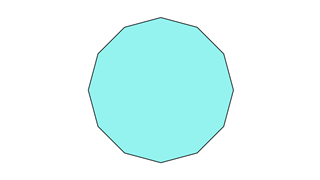
Он состоит из двенадцати равных сторон, а сумма углов равна 1800 градусам. Двенадцать линий симметрии присутствуют.
неправильный многоугольник

Может иметь четыре или более четырех неравных сторон, и внешний вид может быть вогнутым, т.е.то есть, по меньшей мере, один угол больше 180 градусов.
Изогнутые формы
Фигуры, состоящие из изогнутых линий и связанных точек, называются изогнутыми формами. Основные типы, которые включены в эту категорию, описаны ниже:
Круг

Состоящая только из одной изогнутой линии, эта форма не имеет никакой другой точки соединения или вершины. Расстояние от эпицентра до окружности одинаково во всех секторах.
овал / эллипс
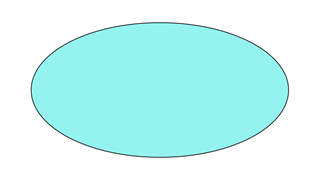
Это похоже на круг, но расстояние от центра до окружности постоянно меняется. Таким образом, эта форма имеет две оси: большую и меньшую вместе с вытянутой формой.
Объектив
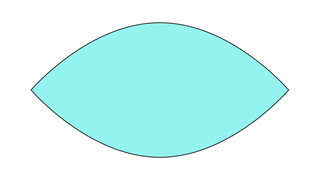
Эта фигура похожа на эллипс, но состоит из двух отдельных изогнутых линий, которые встречаются на противоположных концах.В этом случае две точки присутствуют на их стыке.
Полумесяц
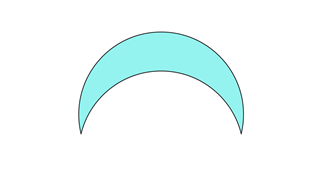
Эта форма характеризуется наличием двух изогнутых линий: одна выпуклая, а другая вогнутая. Они встречаются аналогично линзе, образуя своеобразную фигуру.
Арки
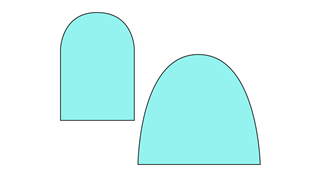
Эти фигуры состоят из изогнутой линии, которая пересекает прямую линию в двух соседних точках.Первая линия может быть полностью изогнутой или может иметь форму двух параллельных линий перед присоединением к прямой линии.
Кольцевое
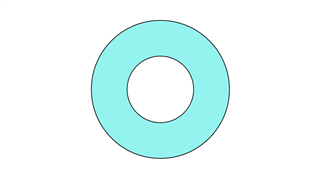
Эта фигура характеризуется наличием двух концентрических круговых структур, каждая из которых отличается по размеру. В большинстве случаев внутренняя часть формы не закрыта. Эта фигура также называется кольцевой структурой.
Круглый сегмент
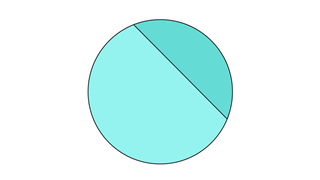
Он в основном определяется как часть круга, который может состоять из части окружности вместе с хордой.Форма может быть полукругом или может быть фигурой с минимальной частью окружности. Оставшаяся часть также может называться сегментом.
Круговой сектор
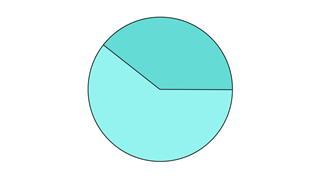
Это в основном определяется как треугольная часть, которая отмечена частью круговой окружности и двумя прямыми линиями. Последние встречаются в общей точке, в основном в центре круга. Их оставшуюся половину круга также можно назвать сектором.
Описанные выше формы являются базовыми, и помимо них существует множество других фигур в категории 2D геометрии. Изучив эти формы, давайте взглянем на различные виды геометрических фигур, относящихся к категории 3D.
Трехмерные (3D) фигуры
куб / шестигранник
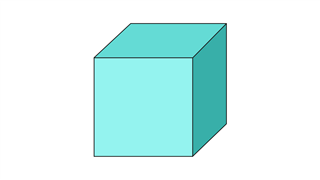
Эта фигура имеет 12 ребер, 8 вершин и 6 граней.Все стороны равны по длине, а лица квадратной формы.
Прямоугольная призма / кубоид
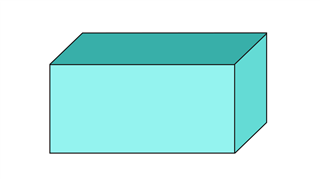
Он имеет те же характеристики, что и куб, в отношении количества сторон, граней и вершин, за исключением того, что грани имеют прямоугольную форму.
Цилиндр
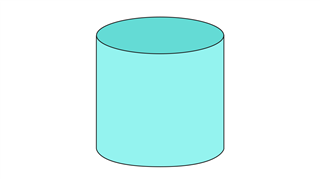
Эта форма не имеет никаких вершин, но состоит из двух плоских граней (только в случае закрытого цилиндра) и одной изогнутой грани.Два ребра также присутствуют.
Сфера
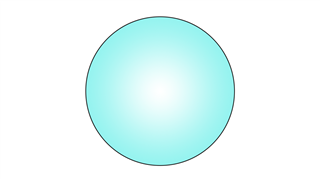
Эта геометрическая фигура не имеет ребер и вершин, присутствует только одна изогнутая грань. Это наиболее равномерно изогнутая форма, включенная в категорию 3D.
Треугольная призма
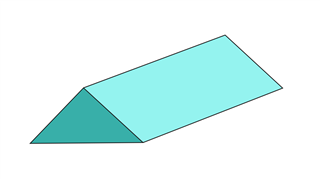
Он состоит из шести вершин, девяти ребер и пяти граней.Грани на обоих концах имеют треугольную форму, тогда как все остальные имеют прямоугольную форму.
Конус
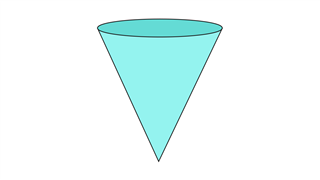
Наряду с одной вершиной и одним краем, конусы имеют одну изогнутую грань и одну дополнительную плоскую грань (в закрытых конусах). Угол вершины может варьироваться от острого до тупого.
шестиугольная призма
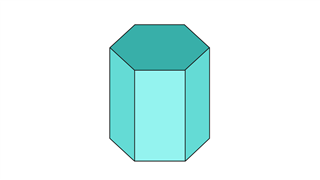
Эта фигура, состоящая из двенадцати вершин, восемнадцати ребер и восьми граней, имеет два шестиугольника на противоположных концах.Остальные грани имеют прямоугольную или квадратную форму.
пятиугольная призма
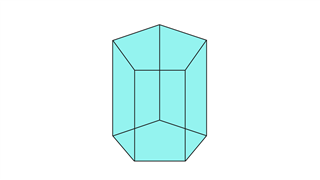
Эта фигура, состоящая из десяти вершин, пятнадцати ребер и семи граней, имеет два пятиугольника на противоположных концах. Остальные грани имеют прямоугольную или квадратную форму.
квадратная пирамида
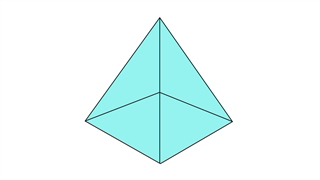
В этой форме основание состоит из квадрата, тогда как остальные грани представляют собой треугольники.В целом, он имеет 5 вершин, 8 ребер и 5 граней.
Треугольная пирамида
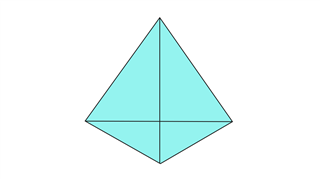
В этой форме основание, а также все грани представляют собой треугольники. В целом, он имеет 4 вершины, 6 ребер и 4 грани. Базальный треугольник имеет другой размер по сравнению с гранями.
Шестиугольная пирамида
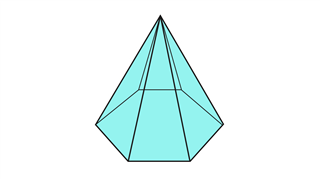
Эта форма состоит в основном из 7 вершин, 12 ребер и 7 граней.Его основание имеет шестиугольную форму, а грани треугольные.
параллелепипед
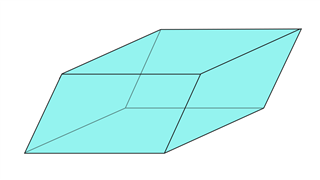
На этом рисунке все грани, а также основание имеют форму параллелограммов. Размеры граней могут отличаться или могут быть одинаковыми.
Тетраэдр
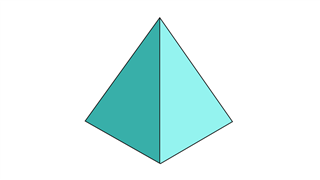
Это похоже на внешний вид треугольной пирамиды, за исключением того, что все лицевые стороны и основание имеют одинаковый размер.
Октаэдр
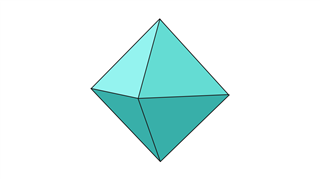
На этой фигуре восемь треугольников, расположенных определенным образом, чтобы сформировать шесть вершин, восемь граней и двенадцать ребер. Треугольники могут быть равносторонними или равнобедренными.
Додекаэдр
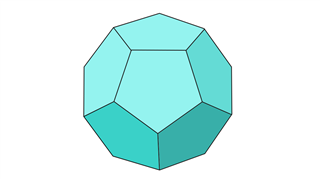
Они состоят из двенадцати пятиугольных граней, двадцати вершин и 30 ребер.Лица пятиугольников одинакового размера.
Икосаэдр
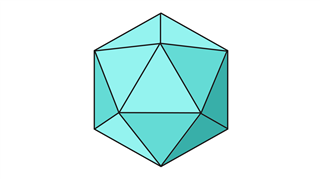
Они характеризуются 30 ребрами, 20 гранями и 12 вершинами. Лица состоят из равносторонних треугольников.
ромбический додекаэдр
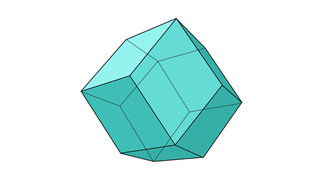
Этот тип фигуры состоит из 12 ромбовидных граней, 14 вершин и 24 ребер.
Frustum

Это конусообразная структура, но вместо вершины на одном конце присутствует круг.
Всестороннее знание геометрических форм и фигур очень важно, особенно если кто-то имеет склонность к этой области математики. Кроме того, нужно научиться следовать различным математическим правилам, которые необходимы при рисовании геометрических фигур. Рисунки, описанные выше, вместе с примерами уравнений, несомненно, помогут вам прояснить основы этой темы.
,
Какие примеры геометрических фигур?
Геометрические фигуры есть практически везде. Независимо от того, где вы смотрите, почти все состоит из более простой геометрии. Ферменный мост состоит, например, из прямоугольников, квадратов и треугольников. Снеговик состоит из кругов с конусообразным морковным носиком.
Эти формы, как двумерные, так и трехмерные, также невероятно важны в контексте изучения математики. Предоставление примеров геометрических фигур научит вас и ваших учеников их функциям и тому, как их лучше понять.
Примеры геометрических фигур
Вот список различных геометрических фигур, а также описание и примеры того, как их можно найти в повседневной жизни.
Круг : круглая форма с таким же радиусом от неподвижной точки в центре.
Например, пирог для пиццы, печенье, колеса велосипедаКвадрат : четыре равные прямые стороны с четырьмя прямыми углами
Например, гараж, квадратные резиновые штампы, плитка на полуТреугольник : Трехсторонняя фигура с прямыми сторонами
e.например, кусок пиццы, кусок сыра, нарезанный в этой форме, бутерброд, нарезанный по диагоналиПрямоугольник : четыре прямые стороны с четырьмя прямыми углами, разной длины и ширины
, например, многоквартирные дома, классная доска, обложка книги, большинство сотовых телефоновПентагон : пять прямых сторон, как правило, одинаковой длины
, например, Пентагон, рисунки на футбольных мячахШестиугольник : шесть прямых сторон, как правило, равных длина
эл.г., ледяные кристаллы, некоторые снежинки, клетки ульяГептагон : семь прямых сторон, обычно равной длины
, например, крышки для коробок для печенья, некоторые типы коробок для таблетоквосьмиугольник : восемь прямые стороны, как правило, равной длины
, например, знак остановки, некоторые зонтики, кольцо UFCNonagon: девять прямых сторон, как правило, равной длины
, например, крышки для некоторых типов бункеров / контейнеров для печеньяDecagon : 10 прямых сторон, обычно равной длины
e.Например, некоторые коллекционные монетыТрапеция: четырехсторонняя фигура с одной парой параллельных сторон
, например, фермы на некоторых мостах, пирамида с отрезанным верхом, ящик для попкорнаПараллелограмм : Четырехсторонняя фигура с двумя парами параллельных сторон
, например, классический ластик, несколько кошельков, структура некоторых мостовРомб : параллелограмм с сторонами равной длины
, например, бейсбольные алмазы, некоторые воздушные змеи, определенные кристаллыЗвезда : многогранный многоугольник с точками и тупыми углами
e.г., звезда Давида, звездные наклейки, звездное ожерелье, звездные печеньяПолумесяц : изогнутая форма серпа, изогнутая и сужающаяся к точке
, например, серповидные валики, луна во время определенных фаз, изогнутая форма на флагах Пакистана и ТурцииОвальный : вытянутый круг, радиус которого на одной оси короче другого, например
, например, яйца, булочки для хот-дога, беговая дорожкаполукруг : круг, разрезанный ровно пополам по его диаметру
e.например, половина печенья, половина пирога для пиццы, другие неполные кружкиЦилиндр : трехмерная фигура с параллельными сторонами и круглым поперечным сечением
, например, картон внутри бумажного полотенца, прямая труба, стакан для питьяПризма: трехмерная фигура, в которой одна пара противоположных сторон имеет одинаковую форму, соединенные прямыми параллельными сторонами
, например, картонная коробка, камеры, зерновая коробка, коробка ТоблеронаПирамида : трехмерная фигура с одной плоской стороной и ребрами, соединяющимися в точке
e.г. Великая пирамида в Гизе, крыша дома
Конечно, некоторые из этих форм взаимозаменяемы. Например, сумка не всегда может быть параллелограммом, так как, безусловно, существуют круглые сумки и другие типы. Этот список также не является исчерпывающим, поскольку существует много других двумерных и трехмерных геометрических фигур.
Цель иметь примеры геометрических фигур, чтобы вы могли видеть, насколько эти фигуры действительно важны в повседневной деятельности.Таким образом, вы можете передавать информацию о практическом применении геометрических фигур любому, кого вы обучаете.
Полигоны и многогранники
«Геометрические фигуры» — это более общий термин, который охватывает все эти типы фигур. Однако, если вы хотите быть более конкретным, фигуры, которые находятся только в двух измерениях (например, квадрат), можно назвать полигонами. Это определяется как плоская фигура, по крайней мере, с тремя прямыми сторонами, обычно создавая закрытую форму.
Когда вы берете это в третье измерение, как с кубом, оно становится твердой фигурой, которую вы называете многогранником.Суффиксы -gon и -hedron могут затем использоваться для определения количества сторон или ребер, например, десятиугольника и десятигранника.
Геометрическая треугольная форма, вырезанная из кирпича сыра.
3D-фигуры — математика GCSE Revision
Трехмерная фигура описывается своими ребрами, гранями и вершинами (вершина — это единственная форма вершин).
Это видео и изображения ниже объясняют грани, вершины и края общих трехмерных форм.
Грани — это двумерная фигура, которая составляет одну поверхность трехмерной фигуры, ребро — это место, где встречаются две грани, а вершина — это точка или угол геометрической фигуры.
Чтобы определить площадь грани трехмерной фигуры, используйте квадратные единицы, такие как см 2 , так как грань трехмерной фигуры является самостоятельной двумерной формой (грань пирамиды образует треугольник или ее основание квадрат).Вы можете узнать, как разработать область формы здесь.
Чтобы определить объем всей трехмерной фигуры, вы использовали кубические единицы, такие как см 3 . Чтобы узнать, как определить объем трехмерных фигур, нажмите здесь.
Свойства трехмерных фигур — Призмы
куб
Число ребер: 12
Количество граней: 6
Количество вершин: 8
Кубоид
Число ребер: 12
Количество граней: 6
Количество вершин: 8
Цилиндр
Число ребер: 2
Количество граней: 3
Количество вершин: 0
Треугольная призма
Количество ребер: 9
Количество граней: 5
Количество вершин: 6
восьмиугольная призма
Число ребер: 24
Количество граней: 10
Количество вершин: 16
Свойства 3D-фигур — Пирамиды
Тетраэдр
Число ребер: 6
Количество граней: 4
Количество вершин: 4
квадратная пирамида на основе
Число ребер: 8
Количество граней: 5
Количество вершин: 5
Пирамида на основе шестиугольника
Число ребер: 12
Количество граней: 7
Количество вершин: 7
Свойства 3D-фигур — изогнутые грани
Конус
Число ребер: 1
Количество граней: 2
Количество вершин: 1
Frustum
Число ребер: 2
Количество граней: 3
Количество вершин: 0
Сфера
Число ребер: 0
Количество граней: 1
Количество вершин: 0
,
2D Геометрические фигуры
- Дом
- > По предмету
- > Геометрия
- > 2D Геометрические фигуры
Фигуры, показанные ниже, могут быть полезными напоминаниями вам, как вам
помочь с домашним заданием геометрии ваших детей. Каждая геометрическая форма
включает краткое описание и иллюстрированный пример.
Список фигур
Форма | Описание | |
| Полигон | Замкнутая фигура из линейных сегментов каждый из которых пересекается ровно с двумя другими отрезками. |  |
| Четырехсторонний | 4-х сторонний многоугольник |  |
| Площадь | Четырехугольник, имеющий все стороны, равные в длина и формирование прямых углов. |  |
| Треугольник | 3-сторонний многоугольник (сумма внутренних углов = 180 °) |  |
| Прямоугольник | 4-сторонний многоугольник со всеми прямыми углами. |  |
| Параллелограмм | 4-х сторонний многоугольник с двумя парами параллелей Стороны. | 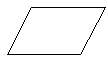 |
| Пентагон | 5-сторонний многоугольник (на рисунке показан обычный шестиугольник с «обычным» значением каждой из сторон равный по длине) | 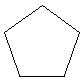 |
| шестигранник | 6-сторонний многоугольник |  |
| семиугольник | 7-сторонний многоугольник | 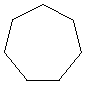 |
| восьмиугольник | 8-сторонний многоугольник |  |
Примечание. Используйте этот генератор печатной миллиметровки для создания сеток, которые могут помочь при рисовании фигур.Вернуться к началу страницы
Подробнее
Math Help
Есть еще геометрия
определения
включены в этот раздел.
Предотвратить издевательства
Нажмите здесь для ссылок на информацию и помощь в борьбе с издевательствами.
Подписаться на рассылку


По
Предмет> Геометрия> 2D-фигуры
,
Развертки геометрических фигур для склеивания: 🛠 Развёртки геометрических фигур 👈
🛠 Развёртки геометрических фигур 👈
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
Геометрические фигуры из бумаги — Вырезаем и занимаемся!
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Также на этой странице вы найдете плоские фигуры для вырезания, из которых нужно сложить замок. Этот учебный материал поможет ребенку наглядно изучить объемные геометрические фигуры: куб, пирамиду, ромб, шестигранник, цилинд и конус. Задание развивает наглядно-образное мышление.
Объемные геометрические фигуры из бумаги — Вырезаем и клеим:
Здесь вы можете скачать объемные геометрические фигуры из бумаги в виде разверток, которые необходимо распечатать на принтере, вырезать и склеить по указанным местам. В результате у вас получатся объемные фигуры: куб, пирамида (трехгранная и четырехгранная), ромб, шестиугольник, конус и цилиндр. На каждой развертке написано название фигуры, чтобы ребенок во время работы всегда мог видеть, какую фигуру он делает. Это очень удобно для обучения, так как дети обычно не любят, когда взрослые по несколько раз повторяют одно и то же. А в этом случае у родителей нет необходимости проговаривать вслух названия фигур.
- Итак, в первом листе мы выложили следующие геометрические фигуры: куб (фигура, поверхность которого состоит из 6 квадратов), трехгранная пирамида (основание пирамиды и 3 грани), четырехгранная пирамида (основание и 4 грани), ромб (фигура, визуально состоящая из двух пирамид, имеющих общее основание).
- Во втором листе вы найдете развертки таких геометрических фигур из бумаги: шестигранник (фигура, состоящая из шести граней), цилиндр (состоящий из свернутого прямоугольника и двух окружностей-оснований) и конус.
Скачать геометрические фигуры из бумаги — развертки для вырезания вы можете во вложениях внизу страницы
Лист 1
Лист 2
Скачайте и распечатайте 2 листа с фигурами, вырежьте их аккуратно ножницами и склейте в нужных местах. Учтите, что у бумажных фигур есть дополнительные места для сгиба и склеивания (у нас они выделены оранжевым цветом). Все оранжевые места вам необходимо согнуть и намазав их клеем вклеить с внутренней стороны фигуры.
После того, как дети, при помощи взрослых, склеят все геометрические фигуры из бумаги, можно продолжить занятие, задавая детям вопросы. Например: «Покажи мне пирамиду. Сколько у нее сторон? Где ее основание? Чем эта пирамида (показываете трехранную) отличается от этой (четырехранной)? Покажи мне цилиндр. Какие предметы он тебе напоминает? Покажи конус. На что он похож? Покажи куб. Сколько у него сторон? Из какой геометрической фигуры состоят его стороны?» — и так далее.
В зависимости от возраста ребенка, можно использовать в занятии различные обучающие материалы. Например, что такое пирамида:
Какие бывают пирамиды. (Пусть ребенок покажет из них те, которые он склеил)
Что такое куб:
Что такое конус и цилиндр. На что они похожи:
Можете также скачать эти обучающие картинки во вложениях.
Плоские геометрические фигуры из бумаги — Строим замок
В этом упражнении вы можете скачать плоские геометрические фигуры из бумаги и построить из них замок, то есть выложить их на столе таким образом, чтобы получился заданный силуэт замка. Для начала скачайте во вложениях бланки с заданием и распечатайте на принтере. Затем вырежьте геометрические фигуры (квадрат, трапеция, полукруг и треугольник), которые даны к этому заданию. Все карточки с заданиями даны с увеличением уровня сложности (от 1 до 6 задания).
Все карточки с замками можно распечатывать на обычной офисной белой бумаге. А геометрические фигуры нужно распечатать на цветном картоне. Если нет цветного картона, можно использовать для распечатки цветную бумагу, а затем наклеить бумагу на лист картона и вырезать фигуры.
После этого подробно объесните ребенку инструкцию к выполнению упражнения.
«Строители, прежде чем строить какое-либо здание, смотрят сначала на его чертеж или схему, в которых показано каким оно должно быть. Такие чертежи бывают разными. Вот например, один из них», — взрослый показывает одну или две игровых схемы замка с нашего задания. — «Тебе нужно мысленно представить из каких частей состоит каждый замок, руководствуясь теми фигурами, которые можно использовать для строительства.» — взрослый показывает все геометрические фигуры, которые заранее вырезаны из цветного картона.
Очень важно начинать занятие, не используя подсказки, то есть нужно закрывать от ребенка геометрические фигуры, которые нарисованы рядом с силуэтом каждого замка. Пусть ребенок сам подумает, какие фигуры и какого размера ему понадобятся для строительства данного замка. И только если он испытвает трудности, можно приоткрыть для него подсказку.
Также не нужно допускать, чтобы ребенок накладывал вырезанные геометрические фигуры из бумаги на силуэт замка, так как при этом он не будет развивать наглядно-образное мышление. Старайтесь, чтобы всю основную работу ребенок проводил в уме, а не методом подбора.
Скачать карточки с плоскими геометрическими фигурами для строительства замка вы можете во вложениях внизу страницы.
Карточка 1
Карточка 2
Карточка 3
Карточка 4
Карточка 5
Карточка 6
Геометрические фигуры для вырезания:
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Рисунки из геометрических фигур — Задания в картинках и раскраски
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических формю
Геометрические фигуры и их названия — Задания в картинках
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Геометрические фигуры — Раскраска для дошкольников
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Плоские геометрические фигуры — Обведи и дорисуй
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Найди формы геометрических фигур в картинках
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — Задание для детей
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Свойства геометрических фигур для дошкольников
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Счет геометрических фигур — Картинки с заданиями
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
Чертежи геометрических тел — Задание для детей
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Счет до 10 для детей дошкольного возраста
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
Игра «Что лишнее? — Геометрические формы»
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Выкройки геометрических фигур из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
КОММЕНТАРИИ
Задали по геометрии: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Тетраэдр, куб и додекаэдр сделала, а вот оставшиеся две никак(((
Еще возникли трудности с склеиванием..
спасибо, хз че бы делал еслиб не этот сайт =»)
Спасибо большое!)))) очень выручили!
Я бы и так не смогла, полезно было ознакомиться.
помогите, как сделать развертку Четырёхугольной пирамиды с основанием — ромб
Как сделать развёртку тора (то есть кольца, вернее, его поверхности)?
Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность — не хватает воображения всё это нарисовать, ведь поверхность тора — это т.н. неразвёртываемая поверхность (вернее, условно-развёртываемая).
Люди, помогите советом или ссылкой, плиз!
Я бы вам посоветовал сходить в магазин и посмотреть как сшиты подобные чехлы для автомобильного руля. Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома подумать как сделать своё.
как сделать усечённую пирамиду
Спасибо за информацию,но не все фигуры изображены.Пошли в 9 класс ,но не в РОссии.Необходима помощь. С уважением,Тамара.
Может глупый вопрос, но как сделать из бумаги шар? т.е. не просто круг, а именно объемный шар? есть ли вообще в природе такая развертка?
Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе.
Дмитрий, это я тоже помню из курса школьной географии 🙂
А вот как сделать из атласа в электронном виде шар в электронном виде, чтобы потом распечатать и наклеить?
Почему не указаны параметры? Длина, ширина и т.д.?
как сделать цилиндр из бумаги помамогите плиз
Большое человеческое СПАСИБО.
Спасибо вам огромное! Очень нужен был конус. Теперь, благодаря вам, я знаю, как его сделать))
фу
дану это проче простого ещебы квадраты делать учили
мне по технологие задали это
спасибо большое. по геометрии 3 выходит а так 4 :DDD
плохо не чё не пойму
развертка паллалеллограмма неправильная 5 лист
можно было бы еще акуратнее , как-то грубо
шар не получился там не правильный чертеж
Спасибо большое)))) Ну очень помогли)))
Велике спасибі.Розгортки допомогли мені при виготовленні геометричних фігур на технологіях.
Спасибо большое, хорошие и удобные развёртки)
Проблема с параллелепипедом на пятом листе решается отрезанием косячной грани и её разворотом в правильную сторону)
Развертка фигур. Может развертка геометрических тел?
красиво можно научиться
thank you very much
Спасибо большое! Ребенку во втором класе уже задали эти фигуры. Спасибо Вам за модели, очень удобно, распечатали, сидит, клеит )
Модели конечно интересные, но люди парятся выполняя их, хотя особо труда не составило мне сделать даже сферу. Сыновьям моим (близнецам) задали сделать фигурки из картона, но я то заканчил политех и по начерталке и проходили развертки этих фигур. А у кого гуманитарное образование? Вот у них то и проблемма.
Полезно для изо в 6 классе
Мне кажется, что у Вашего шестигранника восемь граней, а у пятигранника — семь. И называются эти тела либо призмами, либо усеченными пирамидами( в зависимости от соотношения оснований)
Калинина Наталья
Дидактическое пособие «Геометрические фигуры из бумаги»
Геометрические фигуры из бумаги должен научиться делать каждый! Ведь никогда не знаешь, какие знания тебе могут пригодиться в жизни. В последнее время техника оригами набирает широкую популярность среди детей и взрослых. Но перед тем как делать разнообразные поделки (животных, птиц, растений, маленьких домиков, нужно начать с простых геометрических фигур.
Лучший способ показать ребенку окружающий мир — дать почувствовать его на ощупь, ведь маленькую кроху хлебом не корми — дай дотронуться до заинтересовавших ее предметов, тем более, если это разноцветные геометрические тела оригами, сделанные своими руками. Яркие объемные поделки из бумаги привлекут внимание ребенка и уж точно не дадут заскучать. А Вы незаметно и с задором проведете горячо любимое чадо в мир занимательной геометрии.
Такие замечательные геометрические тела можно сотворить из бумаги или картона! Для этого понадобятся только ножницы, клей и, собственно, бумага. Необходимо просто перенести их на лист и вырезать. Затем склеить в местах склейки и геометрическая фигура готова! Такие геометрические объемные тела не только очень понравятся ребенку. Созданные своими руками вместе с ним, они дадут возможность познакомить ребенка с объемом и проекцией. Вы сможете наглядно продемонстрировать, как несколько обычных треугольников превращаются в пирамиду. Или как квадратики становятся кубом. Предложите ребенку угадать, какая фигура получится из определенной развертки, а затем склейте ее. Это прекрасно развивает пространственное мышление!
Дидактические игры «Геометрические фигуры» Дидактическая игра «Геометрические фигуры» Цель игры: познакомить детей с основными геометрическими фигурами. Материал: карточки с изображением.
Дидактическое пособие «Геометрические фигуры» Обучение самых маленьких детей является наиболее важным периодом в жизни каждого человека. Лев Николаевич Толстой говорил о первых годах.
Дидактическое пособие «Коллекция бумаги» Дидактическое пособие «Виды бумаги». Она бывает документом, плакатом, фантиком, конвертом, альбомом, книгой, упаковкой, письмом,.
Конспект НОД по ФЭМП «Геометрические фигуры» Конспект непрерывной образовательной деятельности «Геометрические фигуры» Автор разработчик: Сайкова Юлия Николаевна. Воспитатель ГБДОУ.
Конспект занятия по ФЭМП для детей старшего дошкольного возраста «Ориентировка на листе бумаги. Геометрические фигуры» Цель: формирование математического мышления, развитие логики. Задачи: Обучающие: -упражнять в ориентировке по отношению к себе, другим объектам,.
>
Чертежи и развертки геометрических тел
МАОУ ООШ с. Комсомольское
Тема урока:
Чертежи и развертки геометрических тел.
Подготовила: Бактыгалиева Н.Р.
ТЕМА УРОКА: Чертежи и развертки геометрических тел.
ЦЕЛИ УРОКА:
Образовательная: закрепить понятие геометрические тела; читать и строить их чертежи геометрических тел;
Развивающая: развивать пространственное видение предмета, умение вычерчивать развёртку и склеивать фигуру.
Воспитывающая: воспитывать аккуратность при выполнении графической и практической работ, усидчивость, терпимость.
Оборудование:
а) для учителя: презентация «проекции группы геометрических тел», учебник.
б) для учащихся: тетрадь, учебник, чертёжные принадлежности.
ТИП УРОКА: урок изучения нового материала
ОБОРУДОВАНИЕ:
а) для учителя: презентация «Чертежи и развертки геометрических тел», учебник.
б) для учащихся: тетрадь, учебник, чертёжные принадлежности, ножницы, клей.
МЕТОДЫ ПРОВЕДЕНИЯ: беседа, выполнение чертежей геометрических тел и разверток, моделирование.
ЛИТЕРАТУРА: « Черчение» Ботвинников А.Д.,Виноградов В.Н., Вышнепольский И.С.
ХОД УРОКА
1.Организационная часть (1 мин)
Очень правильно, очень мудро,
Да не будет помехой лень,
Утром говорить всем: «Доброе … ( утро)»,
Ну, а днем говорить: «Добрый… ( день)».
2. Сообщение темы, целей урока (1 мин)
Сегодня мы продолжим работу с геометрическими телами, тема сегодняшнего урока: «Чертежи и развертки геометрических тел» ». Мы должны вспомнить основные геометрические тела, узнать, как строятся их развертки.
3. Повторение изученного ранее (3 мин)
Давайте вспомним геометрические тела, которые вы изучали на прошлом уроке.
Учитель показывает чертежи геометрических тел и задает вопросы?
1.Как называется геометрическое тело? (цилиндр, куб, призма, конус, призма, усеченный конус.
2. Я называю тела, а вы приводите примеры предметов:
— шар — пирамида — призма — конус — цилиндр | -планеты, мяч, глобус -пирамиды в Гизе -карандаш, кирпич -ведро у пожарных, колпак, рожок мороженного в виде конуса — шайба, банка консервов |
4. Изучение нового материала (10 мин)
На уроке мы должны научиться самостоятельно, выполнять развёртку некоторых геометрических тел.
С развёртками поверхностей мы часто встречаемся в обыденной жизни, на производстве, в строительстве. Чтобы изготовить упаковку для сока, чая, конфет, духов, праздничную коробочку или кулёк надо уметь строить развёртки поверхностей геометрических тел.
Слайд2
Ребята отвечают.
Развертки имеют большое применение на машиностроительных заводах, обувных фабриках, в швейных мастерских. Для изготовления кожухов машин, ограждений станков, вентиляционных устройств, трубопроводов необходимо из листового материала вырезать их развертки
Слайд 3-4
Разверткой называется плоская фигура, полученная при совмещении поверхности геометрического тела с одной плоскостью.
Слайд 5
При построении развертки надо знать сначала истинные, натуральные размеры и форму отдельных элементов предмета на чертеже. В простейших случаях развертки можно вычертить, не пользуясь проекциями предмета. Например, для построения развертки куба достаточно знать размер одного ребра куба.
Рассмотрим построение разверток поверхности некоторых простейших тел
Рассмотрим развертку конуса. Она состоит из боковой поверхности – сектор R+ образующей конуса, угол α подсчитывается по формуле α =360º*d/2R
Слайд 6-7
Рассмотрим развертку цилиндра. Она состоит из трех частей – боковой поверхности и верхнего и нижнего оснований. Боковая поверхность – прямоугольник с размерами высоты и длины, которая высчитывается по формуле С=πd. Нижнее и верхнее основания – окружности с размерами диаметра d.
Слайд 8-9
Для построения развертки куба достаточно знать размер ребра куба.
Слайд 10-11
Для того чтобы выполнить развёртку, давайте определим из каких фигур состоит пирамида.
Боковая поверхность пирамиды состоит из четырех равных треугольников. Для построения треугольника необходимо знать величины его сторон. Равные ребра пирамиды служат боковыми сторонами граней (треугольниками).
Слайд 12-13
Возьмём правильную прямую шестиугольную призму. Все боковые грани призмы – прямоугольники, равные между собой по ширине а и высоте Н; основания призмы – правильные шестиугольники со стороной, равной а. Так как истинные размеры граней нам известны, нетрудно выполнить построение развертки. Для этого на горизонтальной прямой последовательно откладывают шесть отрезков, равных стороне основания шестиугольника, т.е. 6а. Из полученных точек восставляют перпендикуляры, равные высоте призмы Н, и через конечные точки перпендикуляров проводят вторую горизонтальную прямую. Полученный прямоугольник (Н х 6а) является разверткой боковой поверхности призмы. Затем на одной оси пристраивают фигуры оснований — два шестиугольника со сторонами, равными а. Контур обводят сплошной основной линией, а линии сгиба — штрихпунктирной с двумя точками.
Подобным образом можно построить развертки прямых призм с любой фигурой в основании.
Слайд 14-15
Развёртки некоторых правильных многогранников представлены на рисунке: а) куб, б) тетраэдр, в) октаэдр, г) икосаэдр и д) додекаэдр.
Слайд 16
На остальных слайдах вы видите развертки разных геометрических тел.
Слайд 17-19
5.Практическая работа. (20 мин)
Сейчас вам предстоит выполнить развертки различных геометрических тел. У каждого обучающегося к концу урока должна быть – готовая развертка куба, призмы, конуса. На ваших столах лежат схемы выполнения разверток и размеры геометрических тел. Приступайте к работе.
6. Подведение итогов (2 мин)
Что нового узнали на уроке?
С чем познакомились?
Где применяются?
Чему научились?
7. Рефлексия (1 мин)
Понравился вам урок?
Довольны вы своей работой на уроке?
Домашнее задание.
§16.
Доделать развертку, кто не успел, начертить развертку шестиугольной призмы в тетради по размерам.
Муниципальное автономное общеобразовательное учреждение
«Основная общеобразовательная школа с. Комсомольское»
Открытый урок по черчению
по теме: «Чертежи и развертки геометрических тел»
Класс: 8
Дата проведения: 18.03.2017г.
Учитель: Бактыгалиева Н.Р.
Геометрические фигуры из бумаги
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
Рисование развертки:
- Выбираем размеры квадрата — одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
Рисование развертки:
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
Рисование развертки:
- Рисуем прямоугольник на бумаги, в котором ширина — это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D — диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
Рисование развертки:
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм — основание. С каждой стороне дорисовываем боковые стороны — параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
Рисование развертки:
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание — многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
Читайте также:
Развертки геометрических фигур для склеивания с припусками — Topsamoe.ru
Большой выбор развёрток простых геометрических фигур.
Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.
Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.
Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательно ознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.
Для более качественной печати советую использовать программу AutoCAD, и даю вам развёртки для этой программы, а также читайте, как распечатывать из автокада. Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.
Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров 🙂
А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.
Развёртки трёхгранной пирамиды на первом листе для печати.
И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.
Далее шестигранник, склеить его будет ещё проще, чем пирамиды. Развёртки шестигранника на первом листе.
Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.
Развёртки пятигранника на втором листе.
Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.
А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.
Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.
Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.
Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.
Теперь очень сложная фигура – конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.
Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.
Довольно интересная фигура – ромб, её детали на третьем листе.
А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.
Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.
Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.
И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.
На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!
КОММЕНТАРИИ
Задали по геометрии: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Тетраэдр, куб и додекаэдр сделала, а вот оставшиеся две никак(((
Еще возникли трудности с склеиванием..
спасибо, хз че бы делал еслиб не этот сайт =)
Спасибо большое!)))) очень выручили!
Я бы и так не смогла, полезно было ознакомиться.
помогите, как сделать развертку Четырёхугольной пирамиды с основанием – ромб
Как сделать развёртку тора (то есть кольца, вернее, его поверхности)?
Вопрос задан с практической целью, хочу самостоятельно обшить руль машины кожей, но для этого необходимо начертить выкройку, вот тут и возникла трудность – не хватает воображения всё это нарисовать, ведь поверхность тора – это т.н. неразвёртываемая поверхность (вернее, условно-развёртываемая).
Люди, помогите советом или ссылкой, плиз!
Я бы вам посоветовал сходить в магазин и посмотреть как сшиты подобные чехлы для автомобильного руля. Вообще кожа специфический материал, с ней можно делать практически всё, из бумаги такого не сделаешь, поэтому и выкройти тут трудно посоветовать, лучше посмотреть как это уже сделано и дома подумать как сделать своё.
как сделать усечённую пирамиду
Спасибо за информацию,но не все фигуры изображены.Пошли в 9 класс ,но не в РОссии.Необходима помощь. С уважением,Тамара.
Может глупый вопрос, но как сделать из бумаги шар? т.е. не просто круг, а именно объемный шар? есть ли вообще в природе такая развертка?
Развёртка шара из бумаги представляет собой дольки, полоски бумаги сужающиеся по краям. Развёртка шара похожа на рисунок из полосок на арбузе.
Дмитрий, это я тоже помню из курса школьной географии 🙂
А вот как сделать из атласа в электронном виде шар в электронном виде, чтобы потом распечатать и наклеить?
Почему не указаны параметры? Длина, ширина и т.д.?
как сделать цилиндр из бумаги помамогите плиз
Большое человеческое СПАСИБО.
Спасибо вам огромное! Очень нужен был конус. Теперь, благодаря вам, я знаю, как его сделать))
фу
дану это проче простого ещебы квадраты делать учили
мне по технологие задали это
спасибо большое. по геометрии 3 выходит а так 4 :DDD
плохо не чё не пойму
развертка паллалеллограмма неправильная 5 лист
можно было бы еще акуратнее , как-то грубо
шар не получился там не правильный чертеж
Спасибо большое)))) Ну очень помогли)))
Велике спасибі.Розгортки допомогли мені при виготовленні геометричних фігур на технологіях.
Спасибо большое, хорошие и удобные развёртки)
Проблема с параллелепипедом на пятом листе решается отрезанием косячной грани и её разворотом в правильную сторону)
Развертка фигур. Может развертка геометрических тел?
красиво можно научиться
thank you very much
Спасибо большое! Ребенку во втором класе уже задали эти фигуры. Спасибо Вам за модели, очень удобно, распечатали, сидит, клеит )
Модели конечно интересные, но люди парятся выполняя их, хотя особо труда не составило мне сделать даже сферу. Сыновьям моим (близнецам) задали сделать фигурки из картона, но я то заканчил политех и по начерталке и проходили развертки этих фигур. А у кого гуманитарное образование? Вот у них то и проблемма.
Полезно для изо в 6 классе
Мне кажется, что у Вашего шестигранника восемь граней, а у пятигранника – семь. И называются эти тела либо призмами, либо усеченными пирамидами( в зависимости от соотношения оснований)
В основе самых сложных и необычные формы сооружений, устройств, механизмов лежат элементарные геометрические фигуры: куб, призма, пирамида, шар и другие. Для начала научитесь создавать самые простые фигуры, а после вы легко освоите более сложные формы.
Многие моделисты начинают свой путь с бумажных моделей. Это обусловлено доступностью материала (найти бумагу и картон не составляет трудности) и легкостью в его обработки (не требуются специальные инструменты).
Однако, бумага имеет и ряд характерных особенностей:
- капризный, хрупкий материал
- требует высокой аккуратности, внимательности, усидчивости при работе
По этим причинам бумага является материалом, как для начинающих, так и для настоящих мастеров и из нее создаются модели самой разной сложности.
В этот статье мы изучим простейшие геометрические фигуры, которые можно сделать из бумаги.
Вам понадобятся следующие материалы:
- лист бумаги
- карандаш
- линейка
- ластик
- ножницы
- клей ПВА либо клеящий карандаш
- кисточка для клея, лучше из жесткой щетины
- циркуль (для некоторых фигур)
Как сделать куб из бумаги?
Куб – правильный многогранник, каждая грань которого представляет собой квадрат
Создание куба состоит из двух этапов: создание развертки и склеивание. фигуры. Для создания схемы вы можете воспользоваться принтером, просто распечатав готовую схему. Либо вы можете самостоятельно с помощью чертежных инструментов нарисовать развертку.
- Выбираем размеры квадрата – одной стороны нашего куба. Лист бумаги должен быть шириной не менее 3 сторон этого квадрата и длиной немного более 4 сторон.
- Чертим в длину нашего листа четыре квадрата, которые станут боковыми сторонами куба. Рисуем их строго на одной линии, вплотную друг к другу.
- Над и под любыми из квадратов рисуем по одному такому же квадрату.
- Дорисовываем полоски для склеивания, с помощью которых грани будут соединяться между собой. Каждые две грани должны соединяться одной полоской.
- Куб готов!
После рисования развертка вырезается ножницами и склеивайте ПВА. Клей очень тонким слоем равномерно размазываем кистью по поверхности склеивания. Соединяем поверхности и закрепляем в нужном положении на некоторое время, с помощью скрепки или небольшого груза. Срок схватывания клея где-то 30-40 минут. Ускорить высыхание можно методом нагрева, например, на батарее. После склеиваем следующие грани, закрепляем в нужном положении. И так далее. Так постепенно вы проклеите все грани куба. Используйте небольшие порции клея!
Как сделать конус из бумаги?
Конус – тело, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность.
- Рисуем циркулем окружность
- Вырезаем сектор (часть круга, ограниченная дугой окружности и двумя радиусами, проведенными к концам этой дуги) из этой окружности. Чем больший сектор вы вырежете, тем острее будет конец конуса.
- Склеиваем боковую поверхность конуса.
- Измеряем диаметр основания конуса. С помощью циркуля рисуем окружность на листе бумаге требуемого диаметра. Дорисовываем треугольнички для склеивания основания с боковой поверхностью. Вырезаем.
- Приклеиваем основание к боковой поверхности.
- Конус готов!
Как сделать цилиндр из бумаги?
Цилиндр – геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её.
- Рисуем прямоугольник на бумаги, в котором ширина – это высота цилиндра, а длина определит диаметр будущей фигуры. Отношение длины прямоугольника к диаметру определяется выражением: L=πD, где L- длина прямоугольника, а D – диаметр будущего цилиндра. Подставив в формулу требуемый диаметр, найдем длину прямоугольника, который будем рисовать на бумаге. Дорисовываем небольшие дополнительные треугольнички, которые необходимы для склеивания деталей.
- Рисуем на бумаге два круга, диаметром цилиндра. Это будет верхнее и нижнее основания цилиндра.
- Вырезаем все детали будущего бумажного цилиндра.
- Склеиваем боковую поверхность цилиндра из прямоугольника. Даем детали высохнуть. Приклеиваем нижнее основание. Ждем высыхания. Приклеиваем верхнее основание.
- Цилиндр готов!
Как сделать параллелепипед из бумаги?
Параллелепипед – многогранник, у которого шесть граней и каждая из них параллелограмм.
- Выбираем размеры параллелепипеда и величины углов.
- Чертим параллелограмм – основание. С каждой стороне дорисовываем боковые стороны – параллелограммы. От любой из боковой стороны дорисовываем второе основание. Добавляем полоски для склеивания. Параллелепипед может быть прямоугольным, если стороны прямоугольники. Если параллелепипед не прямоугольный, то создать развертку немного сложнее. Для каждого параллелограмма нужно выдержать требуемые углы.
- Вырезаем развертку и склеиваем.
- Параллелепипед готов!
Как сделать пирамиду из бумаги?
Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.
- Выбираем размеры пирамиды и количество ее граней.
- Рисуем основание – многогранник. В зависимости от количества граней это может быть треугольник, квадрат, пятиугольник или другой многогранник.
- От одной из сторон основания рисуем треугольник, который будет боковой стороной. Следующий треугольник рисуем так, чтобы одна сторона у него с предыдущим была общая и так далее. Так рисуем столько треугольников, сколько сторон в пирамиде. Дорисовываем полоски для склеивания в нужных местах.
- Вырезаем и склеиваем фигуру.
- Пирамида готова!
low poly викинг
Существуют три разновидности, но наша задача найти отличия. High poly или высокополигональное моделирование, подразумевает создание объекта с большим числом полигонов( эффект сглаживания),или если сказать по другому—точной его копии. low poly, в переводе низкополигональное моделирование, используется для создания фигуры с небольшим числом полигонов, что придает некий лофт(грубость) модели. Обычно, для экономии ресурсов, когда не требуется высокая детализация, а так же для создания иллюстраций, которые набирают большую популярность в последнее время.
Полигональное моделирование из бумаги
Позволяет визуализировать объект с помощью специальной сетки. Оно появилось в то время, когда для определения местонахождения точки необходимо было вручную вводить её координаты по осям X, Y, Z. Если три точки координат задать как вершины и соединить их ребрами, то получится треугольник, который в 3d моделировании называют полигоном. Как правило, он имеет свою текстуру и цвет, а если объединять несколько,то получится модель. Вместе, они составляют сетку или объект.
Для того, чтобы края модели не имели граненого вида, необходимо, чтобы они были малого размера, а поверхность состояла из маленьких плоскостей. Если предполагается точное моделирование, либо в дальнейшем увеличение его изображения, то необходимо строить модель с большим количеством граней, хотя, если на модель смотреть издали без приближения, достаточно будет небольшого количества. Это и есть полигональное моделирование. Сетка состоит из под объектов и может состоять из огромного количества одинаковых ячеек:
Что бы создать 3D модель необходимо работать (с частями) подобъектами. Объединяем и делим, меняем их форму и размер, вращаем, а также применять другие операции, которые позволяются в специализированном программном обеспечении.
Набор программ для создания и 3D-развертки
Естественно, чтобы получить желаемую фигуру пригодятся специальные программы. Я расскажу о самых актуальных и незамысловатых. Они могут помочь превратить некоторые идеи в красивые творения и прототипы, которые можно использовать в самых разных дизайнерских ноу хау. Эти редакторы доступны для изучения, освоить их сумеют даже новички за короткий промежуток времени. Использование ПО позволило на огромную ступень повысить уровень кинематографа компьютерных игр, дизайна интерьера, архитектурных и скульптурных решений. Выбор оптимального программного обеспечения часто бывает трудным, так как непросто найти подобрать всё в одном, что бы весь необходимый функционал был в одном месте.
Совокупность граней, из которых будет состоять оболочка изделия, являются сеткой. Изготовление несложное, поскольку они имеют четко определяемые внешнюю и внутреннюю область, и поэтому дополнительных параметров и вычислений не понадобится. Но этот способ требует терпения и усидчивости, потому что необходима сосредоточенность, активная мозговая деятельность и тысячи кликов мышкой. Будьте внимательны, даже маленькие погрешности способны испортить процесс.
Pepakura Designer
Умеет работать со множеством форматов 3D моделей, например 3DS, DXF, MQO, LWO. Список можно просмотреть на официальной странице программы, думаю это сделать не сложно.
Как правило такой набор или развертку бородатого воина вы не скачаете в бесплатном доступе. Есть множество профессиональных распечаток, но их можно только приобрести за символическую плату к примеру на площадке Etsy.
Папекура Дизайнер создаёт и редактирует 3D заготовки. Чертеж-выкройку развернутую, которую затем можно вывести на печать в нужном масштабе, вырезать и склеить. Конечно, такой подход подразумевает изрядную работу, но выбирать не приходится — более дешёвого и доступного метода “материализации виртуальных объектов” еще не придумано. Pepakura Designer поддерживает различные форматы 3D моделей созданных в программах 3Dstudio, Lightwave, AutoCad и др. Программа создает развертку 3-х мерного изображения для последующей печати на принтере. Она выдаст рисунок с готовыми местами для склеивания и вырезания.
Pepakura Viewer
Менее мощный инструмент может только просматривать работы, не имея возможности изменять их. Помимо этой прямой функции, вы можете увеличивать, уменьшать, крутить, вертеть, выставлять углы и делать прочие безобидные махинации. Это всё, что потребуется для успешной склейки.
Делаем
модели из бумаги, пепакура для развёртки
На примере кота мы видим, как выглядят схемы и развёртки полигональных фигур. Это также может быть собака, мышка, или другое животное. Для того что бы всё получилось нужен хороший качественный набор в pdf. Как правило бесплатные имеют дефекты, так как создавались новичками, профи уже требуют цену за свой труд.
Натуральный кот и шикарный олень из бумаги. Скульптура в мини-размере для украшения интерьера.
Дизайнерский loft черно-золотой бык в декоре стены. Если вы создаёте крупные фигуры розового слона или большую голову лося вам нужен плотный картон для моделирования.
Черно-белый набор смешных человечков из картона и сложная модель Хаски.
Полигональная фигура их методы и способы построения
Создаются тремя основными методами, которые используют в объединённом варианте и по отдельности. Использование примитивов—за основание берут готовые геометрические фигуры вроде куба или цилиндра. Конструируем нужную модель путем вытягивания подобъектов и деления существующих граней. Также вытягиванием новых граней из полигона-исходника , когда каждый следующий появляется из предыдущего.
Предусмотрено три основных способа построения визуализации.
- Для придания нужной формы меняется положение рёбер, их размеры.
- Проводятся манипуляции с вершинами, их перемещение, удаление и т.д.
- Грани-полигоны используются для более сложных действий. Это придание формам выпуклости или наоборот заостренности. Возможно сглаживание или вдавливание поверхности—работаем с плоскостями.
Необходимый набор для сборки, схемы и развертки полигональной фигуры
Позаботьтесь о хорошем, удобном столе и стуле, нужно, что освещение падало из-за левого плеча, используйте настольную лампу. Чтобы не выпачкать стол клеем застелите его плёнкой или положите лист стекла с зашлифованными краями, чтобы не порезаться. Чтобы научиться складывать базовые изделия, вам понадобятся простые приспособления вроде ножниц, канцелярского ножа, клея ПВА и кисточки для его нанесения.
Отдайте предпочтение строительному клею ПВА — из всех разновидностей у него наиболее густая консистенция, он не портит бумагу, делая её мокрой и вязкой, как обычный. Используются разные виды — от папиросной до обычного картона. Новичкам советуют начинать с акварельной, в 200 грамм на м2 для крупных элементов и чертёжной разновидности 140-160 грамм – при разработке мелких частей.
Бумага для паперкрафта и клей для бумажных моделей
Основным материалом для создания является, естественно, обычная бумага, но так как она не сильно надёжная и хрупкая, советуем обратить внимание на полукартон, либо же обыкновенный картон. Детали из него более крепкие и придают готовому творению износостойкость.
Удивительный кит с подсветкой—эксклюзивный ночник в спальне вашего ребёнка
У каждого мастера имеются свои секреты, вот и мы хотим поделиться с вами открытием.
Но также неплохой связующий предмет для элементов – клеевой раствор. Выбирайте вариант, который удобнее.
Модель из бумаги
Рабочий процесс создания проходит в несколько простых этапов. Перед началом процесса мастер определяется, какую фигурку он хочет сконструировать. На самом деле, можно смастерить практически любое изделие, но бумажное моделирование чаще предполагает такие варианты:
- многогранники с выпуклыми и вогнутыми углами, геометрические фигуры
- копии зданий в масштабе
- макеты автомобилей премиум класса
- танки, тяжелые орудия, бронемашины
- поезда, корабли и подлодки, самолеты
Бумага для моделирования—основной рабочий материал. Следует уделить особое внимание её качеству! Для начального творчества лучше всего использовать обыкновенные листы формата А4, они имеют хорошее качество и является самой белоснежной по отношению к другим маркам. Плотность – 80 г/м. Советую приобретать специальную, для черчения.
Создание макета
Многие укрепляют эпоксидкой или красят краской. Я не рекомендую, потому что лучше взять качественную бумагу и собрать аккуратно, чем некачественно нанести краску из-за чего сгладятся грани, что придаёт грубости. К тому же модели не требуют особой прочности, так как приспособлены для украшения стен. Они собираются из предварительно вырезанных и согнутых деталей. Развертки необходимо распечатывать на бумаге 170—200 г/м². Это сделает её устойчивой.
группа заготовок на рабочем столе
При вырезании каждой детали обязательно нумеровать каждую. Для сгибов используйте линейку. Чтобы придать детали округлость, оберните её вокруг карандаша. От силы скручивания зависит сама форма. Тот же способ используйте для кривых поверхностей.
Сборка: особенности процесса
- иголка для нанесения клея в труднодоступных местах
- papercraft развёртки
- кисточка
- острые ножницы или канцелярский нож
- металлическая линейка
- любая ровная поверхность
- клей (не используйте ПВА, после высыхания он деформирует изделие), но на собственном опыте убедились, что эффективнее использовать двухсторонний скотч, шириной 2 мм, в этом случае обязательно наличие пинцета
- дотс для продавливания сгибов
Для жёсткости деталь по сгибам и пустоты внутри заполняем монтажной пеной, но без фанатизма, чтобы она при расширении не деформировала внешний вид.
Видео-урок “Низкополигональные модели”
Арт-голова оленя станет чудесной маской на маскарад, либо вечеринку.
Сказочный декор для фотостудии.
Полигональная модель и основные рекомендации
Предпочтение отдаем геометрическим фигурам из четырехугольников. Проще в деформации, что позволит сэкономить время,не проводя ненужных манипуляций. Треугольники применяем как можно меньше. Также не стоит использовать сложные геометрические фигуры, с большим количеством ребер и углов, это может привести к деформации текстуры.
Советуем визуализировать только необходимые элементы, построение дополнительных конструкций усложняет, если это мелкие детали, их можно делать, используя текстуры. Эта техника рассчитана на создание объектов с точными формами и чёткими контурами. Маленькие грани строят целостное, они имеют цвет и форму. Указанный способ котируется в промышленном дизайне.
Полигональные изделия из металла или пластика
Множество интересных идей можно воплотить из такого “сурового” материала, как металл или пластмассы. Такие изделия – арт-объекты, они станут великолепным украшением фотозоны, ресторана, дачного участка, коттеджного посёлка, либо парка. Внешний вид фигур ограничен только бюджетом и фантазией заказчика.
Полигональная пантера с эфектом сглаживания.
Лошадь из стеклопластика.
Ben Foster Sculpture
Полигональные фигуры в интерьере и креативные дизайнерские идеи
Практически всеми возможными фигурами можно украшать детскую спальню, офис, спальню, кухню. От вашей фантазии зависит масштаб конструкции, стоит начать с небольших фигур что бы потренитроватся и понять какие недостатки вылезут и после этого приступать к моделям с человеческий рост и выше.
loft papercraft для дома
полигональная фигура в интерьере
лисенок и цветы
Настенная скульптура – бык.
Заяц – отличное дополнение к пасхальной корзинке.
Низкополигональные миры
Наверное, все уже слышали о подобного рода иллюстрациях. В процессе создания объёмного 3D-изделия, она формируется при помощи полигонов. Чем их численность выше, тем реалистичнее будет вид. Раньше всегда ценилась высокая степень проработки изображений и мастера стремились к высокому числу полигонов, заготовки с низким числом были лишь набросками, считались незаконченной работой.
Mat Szulik—удивительный художник и необычайной красоты миры
французская улица, кофейня и дама в шляпе
Christripes
Vitaliy Prusakov
Kirill Kodochigov
Jona Dinges
Для сборки сурового викинга с топором потребуется неделя усидчивости, не меньше.
Paul DOUARD
Gareth David
Jeremiah Shaw
Пример того как можно сочетая два цвета (серый и зелёный) и три простые фигуры дерево, трава и камень создать низкополигональный шедевр, причем масштаб зависит только от вашего воображения и возможностей.
Видео мастер класс создание развертки полигональных фигур
>
развертка. Развертка пирамиды для склеивания. Развертки из бумаги
Прямоугольник, квадрат, треугольник, трапеция и другие – геометрические фигуры из раздела точной науки. Пирамида — это многогранник. Основанием этой фигуры является многоугольник, а боковыми гранями треугольники, имеющие общую вершину, или трапеции. Для полного представления и изучения любого геометрического объекта изготавливают макеты. Используют самый разнообразный материал, из которого выполняется пирамида. Поверхность многогранной фигуры, развернутая на плоскости, называется ее разверткой. Создать макет поможет метод преобразования плоских предметов в объемные многогранники и определенные знания из геометрии. Развертки из бумаги или картона изготовить непросто. Потребуется умение выполнять чертежи по заданным размерам.
Материалы и приспособления
Моделирование и выполнение многогранных объемных геометрических фигур — интересный и захватывающий процесс. Из бумаги можно выполнить большое количество всевозможных макетов. Для работы будут необходимы:
- бумага или картон;
- ножницы;
- карандаш;
- линейка;
- циркуль;
- ластик;
- клей.
Определение параметров
Прежде всего определим, какой будет пирамида. Развертка данной фигуры является основой для изготовления объемной фигуры. Выполнение работы потребует предельной точности. При неправильном чертеже геометрическую фигуру собрать будет невозможно. Допустим, необходимо изготовить макет правильной треугольной пирамиды.
Любое геометрическое тело обладает определенными свойствами. Данная фигура имеет основанием правильный многоугольник, а ее вершина спроецирована в его центр. В качестве основания выбран равносторонний треугольник. Данное условие определяет название. Боковые ребра у пирамиды – это треугольники, количество которых зависит от выбранного для основания многогранника. В данном случае их будет три. Также важно знать размеры всех составных частей, из которых будет составлена пирамида. Развертки из бумаги выполняются в соответствии с учетом всех данных геометрической фигуры. Параметры будущей модели оговариваются заранее. От этих данных зависит выбор используемого материала.
Как выполняется развертка правильной пирамиды?
Основой модели является лист бумаги или картона. Работу начинают с чертежа пирамиды. Фигура представляется в развернутом виде. Плоское изображение на бумаге соответствует заранее выбранным размерам и параметрам. Правильная пирамида имеет основанием правильный многоугольник, а высота проходит через его центр. Изготавливаем для начала простую модель. В данном случае – это треугольная пирамида. Определяем размеры выбранной фигуры.
Чтобы построить развертку пирамиды, основанием которой является правильный треугольник, в центре листа, используя линейку и карандаш, нарисуем основание заданных размеров. Далее к каждой его стороне вычерчиваем боковые грани пирамиды – треугольники. Теперь переходим к их построению. Размеры сторон треугольников боковой поверхности измеряем циркулем. Ножку циркуля ставим в вершину нарисованного основания и делаем засечку. Действие повторяем, перемещаясь в следующую точку треугольника. Пересечение, полученное в результате таких действий, определит вершины боковых граней пирамиды. Их соединяем с основанием. Получаем чертеж пирамиды. Для склеивания объемной фигуры на сторонах боковых граней предусматривают клапаны. Дорисовываем небольшие трапеции.
Сборка макета
Вырезаем ножницами выполненный рисунок по контуру. Аккуратно сгибаем развертку по всем линиям. Клапаны-трапеции заправляем внутрь фигуры таким образом, чтобы ее грани сомкнулись. Их смазываем клеем. Через тридцать минут клей высохнет. Объемная фигура готова.
Развертка четырехугольной пирамиды
Сначала представим, как выглядит геометрическая фигура, макет которой будем изготавливать. Основанием выбранной пирамиды является четырехугольник. Боковые ребра — треугольники. Для работы используем те же материалы и приспособления, что и в предыдущем варианте. Чертеж выполняем на бумаге карандашом. В центре листа чертим четырехугольник с выбранными параметрами.
Каждую сторону основания делим пополам. Проводим перпендикуляр, который будет являться высотой треугольной грани. Раствором циркуля, равным длине боковой грани пирамиды, делаем на перпендикулярах засечки, установив его ножку в вершину основания. Оба угла одной стороны основания соединяем с полученной точкой на перпендикуляре. В результате получаем в центре чертежа квадрат, на гранях которого нарисованы треугольники. Чтобы зафиксировать модель на боковых гранях, дорисовывают вспомогательные клапаны. Для надежного крепления достаточно полоски сантиметровой ширины. Пирамида готова к сборке.
Завершающий этап выполнения макета
Полученную выкройку фигуры вырезаем по контуру. По начерченным линиям сгибаем бумагу. Сбор объемной фигуры производят путем склеивания. Предусмотренные клапаны смазываем клеем и фиксируем полученную модель.
Объемные макеты сложных фигур
После выполнения простой модели многогранника можно перейти к более сложным геометрическим фигурам. Развертка пирамиды усеченной намного сложнее в выполнении. Ее основаниями являются подобные многогранники. Боковые грани – это трапеции. Последовательность выполнения работы будет такой же, как та, в которой изготавливалась простая пирамида. Развертка будет более громоздкой. Для выполнения чертежа используют карандаш, циркуль и линейку.
Построение чертежа
Развертка пирамиды усеченной выполняется в несколько этапов. Боковой гранью усеченной пирамиды является трапеция, а основаниями — подобные многогранники. Допустим, что это квадраты. На листе бумаги выполняем чертеж трапеции с заданными размерами. Боковые стороны полученной фигуры продлеваем до пересечения. В результате получаем равнобедренный треугольник. Его сторону измеряем циркулем. На отдельном листе бумаги строим окружность, радиусом которой будет измеренное расстояние.
Следующий этап – это построение боковых ребер, которые имеет усеченная пирамида. Развертка выполняется внутри нарисованной окружности. Циркулем измеряют нижнее основание трапеции. На окружности отмечаем пять точек, которые соединяют линии с ее центром. Получаем четыре равнобедренных треугольника. Циркулем измеряем сторону трапеции, нарисованной на отдельном листе. Данное расстояние откладываем на каждой стороне нарисованных треугольников. Полученные точки соединяем. Боковые грани трапеции готовы. Остается только нарисовать верхнее и нижнее основания пирамиды. В данном случае это подобные многогранники – квадраты. К верхнему и нижнему основаниям первой трапеции дорисовываем квадраты. На чертеже изображены все части, которые имеет пирамида. Развертка практически готова. Остается только дорисовать соединительные клапаны на сторонах меньшего квадрата и одной из граней трапеций.
Завершение моделирования
Перед склеиванием объемной фигуры чертеж по контуру вырезают ножницами. Далее развертку аккуратно сгибают по начерченным линиям. Крепежные клапаны заправляем внутрь модели. Их смазываем клеем и прижимаем к граням пирамиды. Модели даем высохнуть.
Изготовление разных моделей многогранников
Выполнение объемных моделей геометрических фигур — увлекательное занятие. Чтобы его досконально освоить, следует начинать с выполнения самых простых разверток. Постепенно переходя от простых поделок к более сложным моделям, можно приступать к созданию самых замысловатых конструкций.
Архивы
форм — JDaniel4s Mom
Вы ищете увлекательный способ исследовать формы и цвета вместе со своими детьми? Эти наборы для печати вокруг охоты за мусором дома могут быть именно тем, что вы искали. Они могут начать с поиска объектов определенного цвета, отображаемого на карточке. Определив местонахождение объектов каждого цвета, они могут перемещать один, на котором сосредоточено внимание, для поиска объектов определенной формы.
Что есть в каждом наборе?
Набор «Охота за мусором» содержит вырезанные вами карты.Вырезав карточки, вы можете положить их на кольцо.
В поисках сокровищ
«Охота за сокровищами вокруг дома» сохранена в одном PDF-файле. Вы можете загрузить полный набор и открыть их с помощью программы для чтения PDF, например Acrobat Reader. Затем вы можете решить, какую охоту вы хотите распечатать.
Доступные виды охоты на мусорщиков:
Во-первых, есть набор цветных карточек охоты, на которых изображены цветные карандаши. С этим набором ваши дети могут сразу же начать искать цвета в вашем доме.
Во-вторых, есть набор цветных карточек охоты, на которых изображены неокрашенные мелки. Карточки можете раскрашивать вы или ваш ребенок.
В-третьих, есть набор карточек фигур, на которых отображаются раскрашенные фигуры. Как и цветные карандаши, этот набор готов к печати и использованию.
Наконец, есть набор неокрашенных карточек фигур. Вам решать, нужно ли раскрашивать эти карточки. Карты готовы к использованию, если вы не думаете, что их нужно раскрашивать.
Подготовка карт
Возможно, вы захотите распечатать набор или наборы на карточках, а не на бумаге.Это сделает карты крепче. Ламинирование карточек — тоже отличная идея. Это сделает их более прочными.
Карты можно хранить отдельно или положить на металлическое кольцо. Если вы планируете, чтобы ваш ребенок поискал какой-либо предмет и оставил его на месте, возможно, вам понадобятся карточки на кольце. Если вы планируете, чтобы ваш ребенок просмотрел то, что он нашел и собрал в одном месте, вы можете захотеть снять карточки с кольца.
Предпосылки постройки перед началом «Охоты за сокровищами»
Перед тем, как начать охоту на мусорщиков, вы можете прочитать книгу, в которой есть цвета или формы.Ниже вы найдете несколько замечательных книг, в которых исследуются формы и / или цвета.
Ссылки ниже являются партнерскими ссылками.
Охота на мусорщиков
Есть несколько способов заставить детей поохотиться.
- Могут выдаваться комплектом карточек на кольце или отдельно.
- Детям можно сказать, что они могут искать по всему дому или в отдельной комнате.
- Охоту на мусорщиков можно проводить как внутри, так и снаружи дома.
Вот еще несколько увлекательных учебных заданий:
Кот в шляпе Математические маты
Цифры для золотых монет
Счет до 10 с помощью алгоритма
Сверкающие лазеры соединяют вместе наноразмерные геометрические сетки
Изображение с помощью сканирующего электронного микроскопа самоорганизующейся решетки платины, окрашенное в ложный цвет, чтобы показать двухслойную структуру. Каждый внутренний квадрат наноразмерной сетки составляет всего 34 нанометра с каждой стороны.Предоставлено: Брукхейвенская национальная лаборатория.
На наноуровне, где объекты охватывают миллиардные доли метра, размер и форма материала часто могут иметь удивительные и мощные электронные и оптические эффекты. Создание более крупных материалов, сохраняющих тонкие наноразмерные свойства, — это постоянная проблема, которая формирует бесчисленные новые технологии.
Теперь ученые из U.Брукхейвенская национальная лаборатория Министерства энергетики США разработала новую технику для быстрого создания наноструктурированных сеток для функциональных материалов с беспрецедентной универсальностью.
«Мы можем изготавливать многослойные сетки из различных материалов практически любой геометрической конфигурации», — сказал соавтор исследования и ученый Brookhaven Lab Кевин Ягер. «Быстро и независимо контролируя наноразмерную структуру и состав, мы можем адаптировать характеристики этих материалов.Важно отметить, что процесс можно легко адаптировать для крупномасштабных приложений ».
Результаты, опубликованные в Интернете 23 июня в журнале Nature Communications , могут изменить производство высокотехнологичных покрытий для антибликовых поверхностей, улучшенных солнечных элементов и электроники для сенсорных экранов.
Ученые синтезировали материалы в Центре функциональных наноматериалов (CFN) лаборатории Брукхейвена и охарактеризовали наноразмерную архитектуру с помощью электронной микроскопии в CFN и рассеяния рентгеновских лучей в Национальном источнике синхротронного света — оба офиса Министерства энергетики США.
Новый метод основан на самосборке полимера, при котором молекулы спонтанно собираются в желаемые структуры. Самосборка требует выброса тепла, чтобы молекулы образовали правильные конфигурации. Здесь сильно горячий лазер прошел по образцу, чтобы преобразовать неупорядоченные полимерные блоки в точные конструкции всего за секунды.
«Самособирающиеся структуры, как правило, автоматически следуют молекулярным предпочтениям, что затрудняет создание нестандартной архитектуры», — сказал ведущий автор Павел Маевски, научный сотрудник Брукхейвена.«Наша лазерная техника заставляет материалы собираться определенным образом. Затем мы можем строить структуры слой за слоем, создавая решетки, состоящие из квадратов, ромбов, треугольников и других форм».
Нанопроволока лазерная сборка
Изображение трехслойной платиновой сетки на растровом электронном микроскопе. Цветная вставка показывает каждый отдельный слой наноразмерной сетки. Предоставлено: Брукхейвенская национальная лаборатория.
В качестве первого шага в построении сетки команда воспользовалась преимуществом своего недавнего изобретения лазерного зонного отжига (LZA) для создания чрезвычайно локализованных тепловых всплесков, необходимых для сверхбыстрой самосборки.
Чтобы еще больше использовать мощность и точность LZA, исследователи нанесли термочувствительное эластичное покрытие поверх разобранной полимерной пленки. Тепло от лазера заставляет эластичный слой расширяться — как термоусадочная пленка в обратном направлении — что притягивает и выравнивает быстро формирующиеся наноразмерные цилиндры.
«Конечным результатом является то, что менее чем за одну секунду мы можем создавать строго согласованные партии наноцилиндров», — сказал соавтор исследования Чарльз Блэк, возглавляющий группу электронных наноматериалов в CFN. «Этот порядок сохраняется в макроскопических областях, и его будет трудно достичь любым другим методом».
Чтобы сделать эти двухмерные сетки функциональными, ученые преобразовали полимерную основу в другие материалы.
Один из методов заключался в погружении слоя наноцилиндра в раствор, содержащий соли металлов.Затем эти молекулы накапливаются на самоорганизующемся полимере, превращая его в металлическую сетку. Можно использовать широкий спектр химически активных или проводящих металлов, включая платину, золото и палладий.
Они также использовали метод, называемый осаждением из паровой фазы, при котором испаренный материал проникает в полимерные наноцилиндры и превращает их в функциональные нано-проволоки.
Сотрудники Центра функциональных наноматериалов (слева направо) Атикур Рахман, Кевин Ягер и Павел Маевски изучают точные, специально разработанные наноразмерные сетки.Предоставлено: Брукхейвенская национальная лаборатория.
Послойная решетка
Первый завершенный массив нанопроводов действует как фундамент всей решетки. Дополнительные слои, каждый из которых является вариациями того же процесса, затем укладываются друг на друга, чтобы получить индивидуальные перекрещивающиеся конфигурации — например, заборы из сетки рабицы в 10 000 раз тоньше человеческого волоса.
«Направление лазера, проходящего через каждый несобранный слой, определяет ориентацию рядов нанопроволоки», — сказал Ягер.«Мы меняем направление лазера на каждом слое, и то, как строки пересекаются и перекрываются, формирует сетку. Затем мы применяем функциональные материалы после формирования каждого слоя. Это исключительно быстрый и простой способ создать такие точные конфигурации».
Соавтор исследования Атикур Рахман, постдокторский исследователь CFN, добавил: «Мы также можем накладывать металлы на изоляторы, внедряя различные функциональные свойства и взаимодействия в одну решетчатую структуру.
«Размер и состав сетки имеют огромное значение», — продолжил Рахман.«Например, один слой платиновых нанопроволок проводит электричество только в одном направлении, а двухслойная сетка — равномерно во всех направлениях».
LZA является точным и достаточно мощным, чтобы преодолевать взаимодействия интерфейсов, что позволяет ему управлять самосборкой полимера даже поверх сложных нижележащих слоев. Эта универсальность позволяет использовать широкий спектр материалов в различных наноразмерных конфигурациях.
«Мы можем создать почти любую двумерную решетку и, таким образом, получить большую свободу в создании многокомпонентных наноструктур», — сказал Ягер.«Трудно предвидеть все технологии, которые позволит использовать этот быстрый и универсальный метод».
Сильные лазеры создают сложные самособирающиеся наноматериалы
Предоставлено
Брукхейвенская национальная лаборатория
Ссылка :
Сверкающие лазеры соединяют вместе наноразмерные геометрические сетки (23 июня 2015 г.)
получено 16 июня 2021 г.
с https: // физ.org / news / 2015-06-lasers-snap-nanoscale-geometry-grids.html
Этот документ защищен авторским правом. За исключением честных сделок с целью частного изучения или исследования, никакие
часть может быть воспроизведена без письменного разрешения. Контент предоставляется только в информационных целях.
| Фильтрует список объектов. |
| Выбирает объект, ближайший к указанной точке. |
| Выбирает объекты внутри трехмерного блока, определяемого двумя точками. |
| Селектор, который обрабатывает выбор на основе одного вектора направления. |
| Выбирает объекты параллельно заданному направлению. |
| Выбирает объекты, выровненные в указанном направлении. |
| Выбирает объекты перпендикулярно указанному направлению. |
| Выбирает объекты с заданным типом геометрии. |
| Выберите объект с N-м радиусом. |
| Сортировка объектов в список в порядке, определяемом расстоянием от их центра, проецируемым в указанном направлении. |
| Выбирает ближайшие или самые дальние в указанном направлении объекты. |
| Фильтр для объектов, параллельных (или перпендикулярных) указанному направлению, затем возвращает N-й. |
| Выберите объект (ы) с N-й длиной |
| Выбирает объект (ы) с N-й областью |
| Базовый класс для селекторов, который работает с двумя другими селекторами. |
| Селектор перекрестка. |
| Селектор штуцеров. |
| Селектор разницы. |
| Инвертирует выбор данного селектора. |
| Фильтр отображает объекты, используя простой строковый синтаксис. |
Экспериментальное исследование влияния распределения клея на прочность клеевых соединений | Applied Adhesion Science
Склеивание — это экономичный и легкий метод соединения материалов. Он также обеспечивает меньший вес, более универсальный, устойчивый к коррозии и усталости альтернативу болтовым соединениям и клепкам [1], что делает его очень привлекательным в автомобильной и авиационной промышленности.Потребность в топливной экономичности и более высоких скоростях в транспортных средствах сделала использование композитных материалов популярным. Соединение композитных деталей обычными методами, такими как болтовое соединение или заклепка, вызывает дефекты, такие как расслоение, часто возникающее в процессе сверления отверстий [2]. Клейкое соединение помогает устранить эту проблему. Соединения могут изготавливаться в различных конфигурациях, и соединения внахлест широко используются из-за их эффективности и простоты [3] и часто используются при испытании адгезионных свойств сцепления.
Несмотря на свои преимущества, клеевые соединения подвержены дефектам. Обычными дефектами адгезионного соединения являются пустоты, включения, целующиеся соединения и трещины, которые вызывают снижение прочности соединения [1]. Многие исследователи изучали влияние дефектов на прочность клеевых соединений. Первоначальное исследование влияния дефектов линий связи, таких как зазоры и трещины, было выполнено Харт-Смит [4]. Хеслехерст [5] классифицировал дефекты на две широкие категории, разобщенные и слабые связи, и использовал голографическую интерферометрию для их идентификации.Берри и др. [6] исследовали влияние кольцевых дефектов, центрированных по длине соединения, на прочность соединения. Moura et al. [7] изучали влияние полосовых дефектов, расположенных по центру по длине перекрытия и по ширине, на прочность соединения. Они обнаружили, что по мере увеличения размера дефекта вдоль нахлеста прочность связи снижается из-за более высоких напряжений, возникающих к концу нахлеста. Engerer et al. [8] изучали «ленточные» соединения внахлестку при растягивающей нагрузке. Ленточные соединения внахлест формируются с использованием прерывистых слоев клея по длине или площади нахлеста [9].
Ультразвуковой контроль — широко используемый неразрушающий метод обнаружения дефектов в материале и на границах раздела материалов [10]. Ультразвуковые измерения производятся путем передачи и приема высокочастотных звуковых волн [11]. Анализ данных измерений дает результаты, которые могут помочь идентифицировать наличие границ материала и / или дефектов [12]. Методы импульсного эхо-сигнала широко используются для проверки склеенных швов, особенно при наличии дефектов, таких как пустоты или трещины, поскольку для этого не требуется доступ к обеим сторонам шва [13].Одна из более ранних работ с использованием метода импульсного эхо-ультразвука была сделана Таттерсолом [14], в которой было обнаружено слабое связывание вдоль границы раздела. Shiuh-chan Her и Yi-Chun Li [15] использовали ультразвук для обнаружения слабых связей с эпоксидным клеем, варьируя соотношения смешивания отвердителя, используя различия в частотной характеристике для оценки межфазной жесткости, которая использовалась для определения прочности связи по корреляции. De Freitas et al. [16] использовали акустическую эмиссию для обнаружения слабых связей путем мониторинга механизмов отсоединения в режиме I нагружения с использованием теста с двойной консолью.Многие другие исследователи использовали ультразвук для изучения адгезионных связей [17,18,19,20]. Korzeniowsk [21], например, использовал ультразвук для определения формы и размера дефектов, которые были встроены в адгезивную связку. Это было сделано с использованием разницы в интенсивности звука, отраженного от интерфейса, с использованием данных A-сканирования, в зависимости от того, присутствует ли клей на границе раздела. В текущем исследовании использовалось ультразвуковое C-сканирование для определения формы и размера адгезионного покрытия, что дало лучшее разрешение распределения адгезива.
Разрывы в линии соединения часто возникают из-за недостаточного адгезионного покрытия и поэтому часто рассматриваются как дефект [22]. Эти зазоры вызывают перераспределение приложенной нагрузки на окружающий адгезив, тем самым увеличивая локальное напряжение в этих областях [23]. Оборудование для склеивания, такое как приспособления, рекомендуется, когда клей требует надлежащего контактного давления и / или нагрева [24]. Неправильный выбор или конструкция крепления клеевого шва или небрежность со стороны техника во время процесса нанесения могут привести к неправильному покрытию клеем в области перекрытия клеевого соединения, особенно при использовании жидких и пастообразных клеев.Потеря покрытия соединения во время изготовления может вызвать зазоры в области соединения, которые не могут передавать требуемые напряжения между адгезивами. Настоящее исследование сосредоточено на таких сценариях, когда клей не покрывает всю область склеивания. Форма адгезивного покрытия определялась заранее заданной круглой и эллиптической формой с использованием вырезов в листе политетрафторэтилена (ПТФЭ), поскольку эти формы являются естественными, когда вязкая жидкость распространяется по поверхности под давлением.Перед испытанием склеивания область скрепления сканировали ультразвуком, чтобы определить фактическую форму распределения клея, которая затем коррелировала с ожидаемой формой и размером клея после испытаний на растяжение. Кроме того, данные сканирования можно использовать для создания 3-D (трехмерных) моделей для анализа методом конечных элементов.
Краткий курс по разметке кривых
Нарисуйте кривую
В большинстве проектов по деревообработке используются прямые линии и прямые углы, но иногда вам нужна красиво оформленная кривая, чтобы придать проекту более стильный вид.Так как же сделать кривую, когда вы изменяете план проекта или разрабатываете деталь с нуля? Изучите изогнутые формы хорошей мебели, чтобы развить свой глаз. Тогда попробуйте методы, показанные здесь.
Когда вы возитесь с кривой, пытаясь получить ее именно так, нарисуйте полноразмерный кусок фанеры, ДВП средней плотности, картон или бумагу вместо того, чтобы класть его прямо на свой инвентарь. Вы можете склеить коричневые бумажные пакеты из продуктового магазина, чтобы сделать шаблон настолько большим, насколько это необходимо.Перенесите кривую на заготовку, вырезав шаблон и проведя по его краю.
Для симметричных фигур с несколькими кривыми нарисуйте ровно половину фигуры на фанере, ДВП или бумаге. Вырежьте этот кусок и используйте его как шаблон для второй половины.
Помните, что у вас уже есть набор шаблонов для простых фигур. Например, все, что угодно, от ведра на пять галлонов до небольшой стиральной машины, может служить образцом, когда вам нужен круглый угол. И как только вы создали хороший шаблон, сохраните его.Положите его в ящик или повесьте на перфорированный картон, потому что когда-нибудь он вам снова может понадобиться.
Большие повороты — просто с трамбовкой
Для простого радиуса, который можно найти на некоторых предметах мебели Shaker, не требуется ничего более сложного, чем деревянный брелок и карандаш. Однако без измеренного радиуса по плану или компьютерному чертежу требуется некоторое предположение. Установите ширину на каждом конце выкройки, затем поэкспериментируйте с разной длиной трамплина, пока не получите красивую кривую.Сделайте трамбовку более удобной в использовании, просверлив по ее длине несколько отверстий с разным радиусом. Поместите конец шарнира на обрезок, равный по толщине куску выкройки, как показано на фото вверху этой страницы.
Вот изящный способ нарисовать эллипс для столешниц, подносов и т.п. Используйте квадрат, чтобы отметить пересекающиеся перпендикулярные линии на материале рисунка, например на куске древесноволокнистой плиты средней плотности. Поместите кнопки на длинной оси на равном расстоянии от центральной точки.Свяжите кусок веревки в петлю, оберните ею булавки и поместите карандаш внутрь петли. Держите веревку натянутой, перемещая карандаш по или против часовой стрелки, и вы нарисуете эллипс. Отрегулируйте положение булавок и длину петли, чтобы варьировать размер и пропорции фигуры.
Радиусы чертежа
Изогнутый край этого кронштейна для полки состоит из трех радиусов в 1 дюйм. Это пример, казалось бы, сложной конструкции, которую можно быстро нарисовать с помощью циркуля.Чтобы сделать такой узор, определитесь с его длиной и шириной, а затем используйте эти границы для определения точки A в качестве центра каждой кривой. Установите компас на желаемый радиус, поместите его точку поворота на каждую отметку и нарисуйте кривые.
Вы, вероятно, столкнулись с кривой французского в какой-то момент в школе, но, возможно, вы совсем забыли об этом. Это напоминание о том, что он может пригодиться при проектировании мебели и других проектах по обработке дерева. Самый простой способ применения этого пластикового инструмента — нарисовать угол, не являющийся радиусом, как показано здесь.Если вам нужно повторить форму, наклейте липкую ленту на французскую кривую, чтобы отметить начальную и конечную точки. Вы можете купить набор из четырех французских кривых, охватывающих самые разные формы.
Положитесь на гибкую кривую, чтобы создать точную форму, которую вы задумали, как показано здесь, или используйте ее для переноса кривых из планов или существующих деталей. На пластиковой поверхности находится свинцовый сердечник, который сохраняет практически любую форму.
Если вам нужно продублировать эту кривую на другой половине заготовки, вырежьте узор ленточной пилой.Обведите узор на одном конце заготовки, переверните узор и обведите другой конец, как показано на вставке.
«Побережье Новой Зеландии» Синтии Озик
Но Джордж эмигрировал в Новую Зеландию. Он сказал, что у его положения там есть будущее. Хотя сейчас он находился на средней ступеньке в большой университетской библиотеке в Окленде, через пять лет, как он предсказывал, он станет ее директором. Благодаря изобретательности и дальновидности он оказался в самой первой библиотеке, оцифрованной не только в Новой Зеландии, но и во всем мире.Новая Зеландия была образцом, и именно в связи с этим революционным переходом он был отправлен в качестве связного в Нью-Йорк с поручением, требующим осмотрительности. Его ценность была признана. Директор устроил ему пребывание в Вальдорфе, конечно, для облегчения встреч, но также и для его личного комфорта.
Сама Эванджелина рассказала неожиданную историю. В этом заброшенном районе, где по пятницам после обеда группы детей и их матерей собирались под зонтиками (казалось, всегда шел дождь) в ожидании зеленого грузовика и его груза, она тоже увидела свое неминуемое счастье.Она видела начертания геодезистов на тротуарах вокруг заброшенной старой станции комфорта, предназначенной для ремонта. Это было невысокое красивое бетонное здание в стиле греческого храма; Потертые резные изображения Гигеи, богини здоровья, и Амфитриты, богини воды, пересекали фриз ниже фронтона. Судя по виду, вы не могли представить, что когда-то здесь были общественные туалеты. Он обещал Эванджелине, что грузовик с помятыми крыльями и поврежденными дождем книгами будет обналичен, и ей скоро разрешат войти в дом.
«Помазание», — сказал Джордж. «От донного фидера до королевской рыбы». Эванджелина знала, что это означало, что он не особо задумывался о ее перспективах. Она подводила свою одинокую волю.
Они оставили скамейку и вместе пошли на вокзал. Согласно Пакту, его сторонники были обязаны разойтись сразу после завершения процедуры воссоединения; никто не должен был шпионить за пунктами назначения других. Но тут ничего не поделаешь: им приходилось садиться в один поезд, а из-за большого скопления людей в час пик приходилось сидеть в одном вагоне.Джордж направлялся в Гранд Сентрал на Манхэттене, чтобы добраться до Уолдорфа и Эванджелины до остановки Фордхэм в Бронксе. Они даже нашли места прямо напротив прохода.
Наклонившись, Эванджелина спросила: «Но мы еще не решили, где встретиться в следующий раз. Или когда.
«Как всегда в ту же дату».
«Откуда ты знаешь, что сможешь приехать? Что, если университет вас не присылает? »
«Как оказалось, у меня другая причина. Семейная причина. Я рассказывала вам о своем дяде.
Он имел. Он сказал всем троим при их первой встрече в греческом ресторане; он рассказал им все до мелочей о том, что он называл своей испорченной, но яркой родословной. Его родители покончили жизнь самоубийством. Бок о бок, как Стефан Цвейг и его жена Лотте в Петрополисе, они приняли яд. Тогда он был двухлетним ребенком. Он ничего не знал об этом в течение многих лет, только то, что его мать и отец на самом деле не были его матерью и отцом: они были его двоюродной бабушкой и двоюродным дедом. Они оба были очень старыми, а его тетя умерла.В расцвете сил они были водевилями. Их шкафы были забиты сценической одеждой. У Джорджа часто были свои обеды за кулисами. Он признал, что Вальдорф был приятным человеком, но он предпочел бы остаться со своим невозрожденным дядей, которому девяносто девять лет все еще хотелось выступить.
Никто из других не знал, где находится Петрополис. Оливия догадалась о Греции, но Эванджелина сказала: «Два самоубийства? Один был бы чрезмерным, но два — чрезмерно ».
Руби спросила: «Это Оскар Уайльд?»
«Эванджелина, какая ты бессердечная», — сказала Оливия.И все же Джордж был не против: его наследие было необычным. Это было то, что он искал. Он знал, что он спорт, смелая мутация. Он встал на пропасть жизни, и, если Эванджелина хотела посмеяться, с ним все было в порядке. Он знал, что это было из зависти.
Поезд врезался в станцию Фордхэма.
«Здравствуйте? Привет? Я думаю, ты молчишь? »Мультфильм Бенджамина Шварца
« Хорошо, — сказала Эванджелина, — в тот же день, но где? »
«То же место».
«А там ничего нет!» — позвала она, выходя из машины.
«Будет», — крикнул он в ответ.
Недавно построенная библиотека имела лабораторный вид, гладкая и металлическая. Это выдало все, что запомнилась библиотечной школе. Исчезли обшитые деревянными панелями стены, исчезли деревянные ящики с рядами рукописных учетных карточек. Исчезли карандаши с переутомленными резиновыми штампами даты на концах. Исчезли следы от зимних ботинок (здесь они не оставили следов на всепогодном ковре), а летом исчез отрывистый скрип антикварных вееров, поворачивающих шеи из стороны в сторону.Вместо этого: ряды компьютеров с их холодными лицами, кондиционерами и взрывами гусиных прыщиков. Вежливые молодые люди с научными степенями — первая мышь и вторая мышь — за стальными столами. Из-за стеклопакетов никогда не чувствовалось запаха дождя.
Эванджелина обвинила Гигею и Амфитриту в разрешении этого вторжения; с тех пор они были удалены как непригодные для современного здания. Сантехника была новой, в храме не было никаких богинь. Посетителей снисходительно называли покупателями, как если бы они пришли поспорить о стоимости помидоров на рынке.Детская комната располагалась в месте, где раньше располагались женские туалеты, вдали от тихого центра. И, в отличие от воплей и шума, которые встретили зеленый грузовик, когда он свернул в поле зрения, здесь было тревожно тихо. Многие из клиентов казались любителями, или полусумасшедшими чудаками, догоняющими свой сон, или одинокими браузерами, ищущими духовной помощи.
Наиболее типичные клиенты приходили и уходили со своими пустыми пластиковыми пакетами для продуктов, но самые настойчивые были любителями.Они приходили в десять утра и сидели за столами для чтения до четырех часов дня. В основном это были пожилые вдовы, копирующие образцы игл, или энтузиасты генеалогии, надеющиеся найти королевского предка, или фермеры на заднем дворе, которые выращивали картофель в горшках и изучали возможность пчеловодства.
Но одна из этих странностей оказалась на поколение моложе остальных и появлялась только один день в неделю, обычно незадолго до закрытия. Он был среднего роста и обычно носил потрепанный холщовый портфель.На нем фуражка моряка — аффект, решила Эванджелина, призван противодействовать посредственности. Он проводил не более получаса с блокнотом и, что примечательно, с детской коробкой цветных карандашей, рассматривая красочные фотографии в больших объемах и делая заметки. Она видела, что его предметом были птицы, каждый раз новую птицу. Его рисунки были умеренно талантливыми. Он использовал все мелки в коробке. Хотя он всегда приходил поздно, он редко задерживался; но однажды, торопясь собирать вещи, когда свет уже был выключен, он оставил одну из своих бумаг.Он незаметно соскользнул со стола на пол.
Эванджелина подняла его. Это было изображение птицы с розовыми ногами и желтыми перьями на груди, а под ним заглавными буквами было написано « МАЛЕНЬКИЙ ФЛАЙКАТЧЕР ».
«Я сохранила это для тебя», — сказала она ему, когда он пришел в следующий раз. «Я думал, ты скучаешь по нему».
«Он вымер, — сказал он, — так что действительно пропал. Вы можете увидеть это только в Одюбоне ».
«Вы художник?» — спросила она, хотя и сомневалась в этом.У него не было вида художника. Он сказал, что его интересует наблюдение за птицами, и это была лишь иллюзия его любителя, что когда-нибудь он сможет обнаружить настоящую мелкоголовую мухоловку. Оказалось, что он был учителем математики в соседней средней школе. Она вежливо спросила его, какие предметы он преподает. Он сказал, что элементарная алгебра, промежуточная алгебра, геометрия, тригонометрия, сферическая тригонометрия и, для продвинутых студентов, введение в исчисление. Его чтение было настойчиво точным.
Оскар Нимейер определил современную Бразилию.Теперь художник переосмысливает один из своих домов.
В ту ночь меня пригласили на ужин Вареджао и Буарк. Мне любопытно увидеть дом таким, каким он был задуман: полный людей, несовершенный какой-то кинетической небрежностью. Когда я приезжаю, открытые бутылки с вином покрываются потом в ведерке со льдом под картиной Лигии Кларк. Я сижу в кожаном кресле Лины Бо Барди. Varejão предлагает традиционную еду, которую мы едим на большом обеденном столе, сделанном Серхио Родригесом — picadinho (тушеная говядина) и запеченная рыба, рис и бобы, банановое пюре, жареные перепелиные яйца и нарезанная капуста из загородного сада Varejão. друзья, кинорежиссер Вальтер Саллес и его жена художница Мария Клабина.Друзья Вареджао и Буарка — художники, певцы, музыканты, писатели — мы обсуждаем все, от романа Джойсана Жоао Гимарайнша Росы «Дьявол, который платит в глуши» (1956) до пессимизма, который сегодня окружает бразильскую политику. Возможно, модернизм стал пустым выражением буржуазных вкусов, но здесь он ощущается воодушевленным, заряженным. Мне много раз говорили, что я должен посетить Бразилиа, который находится менее чем в двух часах езды на самолете.
Вместо этого на следующий день я иду в дом, построенный для себя Нимейером в Рио в 1953 году.Он проходит мимо Леблона, богатого прибрежного района, в Барра-де-Тижука, еще одном богатом прибрежном районе. По моей извилистой дороге я вижу фавелы. Это тоже Рио, где безмерная бедность граничит с огромным богатством. Нимейер презирал деньги, даже если работал с теми, у кого они были. Он редко писал о частных резиденциях, которые он спроектировал, и разрешил иллюстрировать или перечислять лишь некоторые из них — как и в случае со многими известными архитекторами, он в значительной степени считал эти проекты исключениями, одолжениями или единовременными.
Добавить комментарий
Any Queries? Ask us a question at +0000000000
