Развертка параллелепипеда для склеивания распечатать: Параллелепипед — объёмное геометрическое тело

Схема параллелепипеда из бумаги распечатать. Как сделать из бумаги параллелепипед и куб? Учимся делать геометрические фигуры вместе с детьми

Как сделать параллелепипед из бумаги, схема (видео, фото)?

Для того чтобы сделать параллелепипед из бумаги своими руками вам потребуется следующее:

ножницы, линейка, карандаш, лист плотной бумаги и вот эта схема.

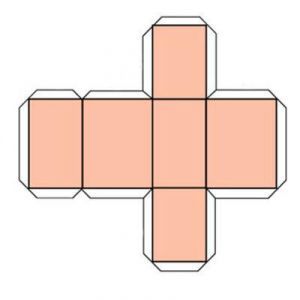
Вырезаем из бумаги вот такую деталь и при помощи клея ПВА и кисточки склеиваем, и получаем аккуратный и ровный параллелепипед.

Параллелепипед — это объёмная геометрическая фигура, имеющая 6 граней (противоположные грани являются параллельными друг другу), каждая из них является параллелограммом.

Самый известный тип параллелепипеда — это прямоугольный параллелепипед, у него все грани являются прямоугольниками.

Форму прямоугольного параллелепипеда имеет немало вещей, с которыми мы сталкиваемся в жизни — коробка, пачка бумаги, шкаф, спичечный коробок и многие другие.

Чтобы сделать параллелепипед из бумаги, нужно воспользоваться развёртками.

Вот как выглядит развёртка прямоугольного параллелепипеда:

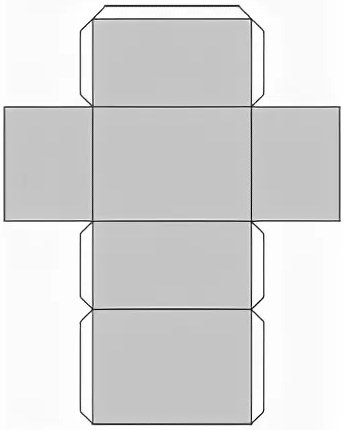
Её вполне можно начертить на бумаге самостоятельно с нужными вам размерами.

Главное помните, что у вас должно получится 3 пары равных по размерам прямоугольников (или 2 пары равных между собой прямоугольников для боковых граней + 2 квадрата одинаковых размеров для оснований).

Гораздо удобнее, когда на развёртке вспомогательные клапаны (это специальные полоски для соединения граней).

Вот этапы создания параллелепипеда:

1) Сначала нужно «перенести» развёртку на лист бумаги (или картона).

Проще всего будет распечатать уже готовую схему (развёртку) на принтере (увеличив его до нужных размеров).

А можно, как я сказал выше, начертить всё самим.

2) Вырезаем развёртку ножницами.

3) Теперь аккуратно сгибаем развёртку по линиям сгиба: всего будет 5 таких линий + 7 линий для вспомогательных клапанов.

4) Наконец, соединяем все грани и склеиваем их.

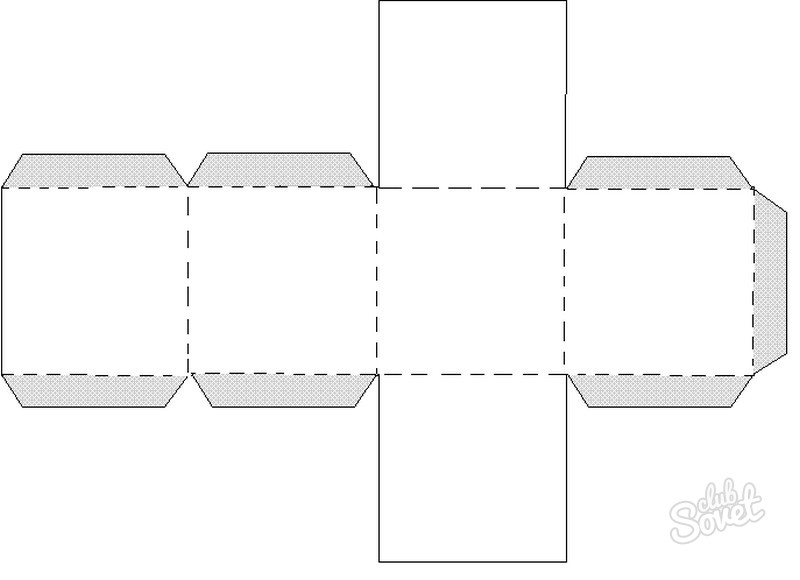
Также предлагаю развёртку для наклонного параллелепипеда:

На выходе получится уже несколько другая объёмная фигура, но всё делаем по тому же самому принципу, что и в случае с прямоугольным параллелепипедом (переносим развёртку — вырезаем — сгибаем — соединяем и склеиваем).

Параллелепипед бывает прямоугольный и обычный. Рассмотрим, как можно научиться делать любые параллелепипеды, то есть с любым углом.

Сначала вычерчиваем на бумаге боковую сторону параллелепипеда, то есть ту, у которой может быть острый угол (на рисунке обозначено как a). Вычерчиваем такую, какая нам нужна. Затем подкладываем под эту бумагу ещё один лист, то есть чтобы получилась двойная бумага. Легче даже сначала сложить лист бумаги пополам, а потом уже чертить. Затем вырезаем эту сторону. Так как у нас был двойной лист, то получилось сразу две одинаковых четыреугольных фигуры.

Затем на одинарной бумаге вычерчиваем выкройку b. Она должна быть с прямыми углами. Её стороны должны быть равны тем сторонам боковых поверхностей, как обозначено на рисунке. Одинаковые стороны обозначены одинаковыми линиями.

Затем обводим эту фигуру линией с отступом, чтобы начертить линию сгиба, которая будет промазываться клеем. Затем вырезаем эту фигуру, чтобы получилось как на рисунке b. Затем складываем две дальние стороны этой выкройки и склеиваем их чтобы фигура сомкнулась. Предварительно перед этим складываем все части сгибов, чтобы они стали угловатые. Затем промазываем части выкройки b, выделенные под клей. И прикладываем к обоим сторонам обе a части.

Размеры на приведённом рисунке схематичны, вообщем их не нужно выводить на принтер и использовать в качестве выкройки, так как они рисовались в Пеинте, а не по размерам.

Как сделать из бумаги параллелепипед и куб? Учимся делать геометрические фигуры вместе с детьми

Изучать геометрию дети начинают в средней школе, а вот первое знакомство с геометрическими фигурами происходит еще в раннем детстве. Как объяснить своему почемучке, что такое параллелепипед? На словах кроха вряд ли поймет. Нужна наглядность. Мы расскажем, как сделать из бумаги параллелепипед, а вы сможете применить эту информацию с пользой.

Сложное название – простая фигура

Как сделать параллелепипед из бумаги? Схема его очень проста, если вы знаете, о чем идет речь. С ранних лет малыши начинают активно познавать этот мир. А все окружающие нас в пространстве вещи – это те или иные геометрические фигуры. Чтобы кроха понимал, что представляет собой параллелепипед, ему нужно показать его наглядно. Для этого можно смастерить фигуру из бумаги.

Но перед этим давайте освежим в своей памяти, что параллелепипед – это призма, которая состоит из параллелограммов. Чтобы малышу было интереснее, используйте для моделирования цветную бумагу и шаблон.

Необходимые материалы:

• лист бумаги;
• шаблон;
• клей.

Пошаговое описание творческого процесса:

• Прогресс не стоит на месте, и персональный компьютер уже есть в каждом доме. А без глобальной сети люди не могут жить практически с пеленок. Находим подходящий шаблон, задаем нужные параметры, распечатываем.

• Обратите внимание, что на шаблоне есть закругления, именно они будут склеиваться с основными гранями фигуры, тем самым сохраняя ее форму.
• Сгибать грани параллелепипеда нужно по пунктирным или внутренним сплошным линиям. Вы поймете, ведь все сложится само собой.
• Вырезаем шаблон и приступаем к склеиванию.
• На каждой линии делаем сгиб, чтобы грани параллелепипеда были одинаковыми и ровными.
• С помощью кисточки и обычного клея фиксируем отдельные части фигуры в единое целое.

Если вы оглянетесь вокруг, то увидите, что в вашем доме многие предметы имеют форму параллелепипеда, например, спичечный коробок.

Необычный вариант конструирования фигуры

Как сделать из бумаги прямоугольный параллелепипед? Вырезать шаблон и склеить стороны фигуры – это просто. Если вы любите проводить свободное время за моделированием всяких поделок, предлагаем вам не совсем обычный вариант параллелепипеда. Его особенность в том, что изначально фигура будет плоской и непохожей на шестигранник, а вот немного воздуха моментально превратит бумагу в настоящий параллелепипед.

Необходимые материалы:

Пошаговое описание творческого процесса:

• Стандартный лист формата А4 имеет прямоугольную форму. Нам нужно сделать заготовку в виде квадрата.
• Сначала складываем обрезанный лист пополам. Хорошенько отпечатываем сгиб.
• Развернем лист и согнем его пополам, только уже с другой стороны.

• Повторяем описанные действия, загибая квадратный лист от углов.
• Так нужно сделать со всех четырех сторон.

• У нас получилось много согнутых линий.
• Находим вершину этих линий и фиксируем рукой.
• Остальные линии загибаем по сделанным ранее сгибам внутрь. У нас должен получиться вот такой треугольник.

• Поворачиваем фигуру на 90° и приподнимаем противоположные уголки.

• Теперь нам нужно превратить эту фигуру в продолговатый ромб.
• Выступающие уголки с правой и левой стороны загибаем к центру. Они должны соприкасаться.
• Еще раз хорошенько приглаживаем все сгибы.

• Перевернем фигуру на другую сторону и выполним аналогичные действия.
• Теперь внимательно посмотрите на рисунок и с максимальной точностью повторите загиб уголков.

• Если присмотреться, то по обе стороны от сделанных загибов есть прорези — своеобразные кармашки. Закладываем уголки в эти кармашки.

• Пока эта фигура не слишком похожа на параллелепипед, ее нужно надуть. Для этого можно воспользоваться трубочкой для коктейлей.
• Воздух нужно задувать через отверстие, которое образовалось на одной из граней фигуры.

Кубики – игра родом из детства

Жалко, когда малыш теряет свои игрушки. Еще хуже, если он их ломает. Вы можете помочь своему крохе сделать оригинальные кубики из бумаги. Предложите малышу раскрасить их. А если вы подключите фантазию, то можете сделать из кубиков отдельные части картинки, которую нужно, как пазл, собрать в единое целое.

Сейчас вы узнаете, как сделать из бумаги параллелепипед и куб. Многие считают, что это одно и то же. На самом деле куб – самая распространенная и простая трехмерная фигура.

Необходимые материалы:

• ручка или карандаш;
• лист бумаги;
• ножницы;
• линейка;
• клей.

Пошаговое описание творческого процесса:

• Кладем лист бумаги перед собой.
• Берем в руки линейку и начинаем чертить прямую линию в нижней части листа, отмеряя отрезки каждые 7 см.

• Выбираем нужную для себя высоту и прочерчиваем параллельную линию. Точно так же делаем отрезки длиной по 7 см.
• Соединяем между собой противоположные точки отрезков. У нас получаются вот такие квадратики.

• От третьего прямоугольника слева начертим еще два: один — вверху, другой — внизу. Достаточно просто удлинить линии до конца листа.

• По контуру вырезаем нашу заготовку.

• Теперь каждый квадратик нужно загнуть. Если у вас не получается пальцами сделать ярко выраженные сгибы, можно воспользоваться линейкой. Не переусердствуйте, иначе порвете бумагу.

• По сгибам фигура отлично складывается в куб.
• Соединим в единое целое все стороны с помощью обычного скотча.

• В результате у нас получился вот такой бумажный куб.

Читайте также:

Конструировать из бумаги различные фигуры несложно. Вы сразу убьете двух зайцев: объясните малышу, что такое геометрические фигуры и как они выглядят, а также отлично проведете время за моделированием параллелепипеда или куба. По аналогии можно сделать многогранники из картона. Творческих вам успехов!

Читайте другие интересные рубрики

Параллелепипед из бумаги: три технологии на одной страничке

Может оказаться немало причин, когда нужно самому сделать параллелепипед: школьное домашнее задание по выполнению модели простейшего геометрического тела, желание смастерить своими руками упаковку для подарка или даже неповторимое оформление домашнего интерьера.

При чем здесь трехмерный многоугольник?

Прямо говоря, все это под силу такой простой форме, как параллелепипед. Из бумаги его сделать проще и быстрее всего. Рассмотрим наиболее интересные варианты: склейка фигуры из выкройки по заданному чертежу, оригами и модульная сборка.

Урок № 1: объемная модель

Для того чтобы сделать прямоугольный параллелепипед из бумаги, понадобится картон, линейка, карандаш и ножницы.

Прежде всего, вы должны точно знать, какого размера модель хотите получить. На отдельном листочке запишите основные размеры параллелепипеда: высоту боковых поверхностей, длину и ширину.

Далее воспользуйтесь примером чертежа:

Важно не просто перечертить образец, а по нужным параметрам. Тогда в результате не произойдет разочарования и необходимости делать двойную работу.

Когда ваша схема будет готова, под линейку обведите полученный чертеж острием ножниц. Это необходимо сделать для того, чтобы картон в местах сгиба аккуратно складывался, а не «диктовал» свои линии.

Перед вами развернутый параллелепипед. Из бумаги своими руками вырежьте заготовку. Сложите ее с обратной стороны по обозначенным линиям.

Осталось лишь изнутри приклеить боковые припуски к прилегающим сторонам модели и ваш параллелепипед готов.

Урок № 2: Оригами

В детстве вам наверняка доводилось играть кубиками. Конечно, в то время вы не догадывались, что имеете дело с параллелепипедами. В процессе игры до параллельности всех сторон нет никакого дела, зато важны функциональные возможности. Да и не выговорить ребенку сложного слова. Главное, что восторг детства можно повторить, но уже на новом уровне. Как? Сделать параллелепипед из бумаги, воспользовавшись техникой оригами. Да не одну модель, а столько, сколько лампочек на вашей галогеновой гирлянде. Посмотрите, что в итоге у вас получится.

Возьмите квадратный лист бумаги. Согните его пополам. Разверните и еще раз сложите с другой стороны.

Повторите те же действия, только в направлении от углов.

Держите пальцами две противоположные стороны листа по центру. Две другие противолежащие поверхности тоже устремите друг к другу и пригладьте полученный треугольник, зафиксировав тем самым новые линии сгиба.

Сначала с одной стороны, а затем и с другой поднимите углы треугольника к вершине.

Получился так называемый ромб. Сведите его правый и левый углы в центре. Снова разгладьте будущий параллелепипед из бумаги.

Сделайте обратное действие. Приоткройте только что согнутые уголки и сложите другие. Они образуются из свободных концов бумажного листа и направляются вершинами к линиям сгибов в противоположные друг от друга стороны.

Все это сложно для понимания лишь до момента, пока вы не увидите, о чем, собственно, идет речь.

Вставьте только что полученные уголочки в образовавшиеся кармашки, как показано на примере.

Итак, параллелепипед из бумаги готов! Просто он пока еще в сложенном состоянии. Придать ему объема можно двумя способами. Первый: надуть. Второй: взять длинный стержень от обыкновенной шариковой ручки и воспользоваться им. Оба способа осуществляются через единственное отверстие, которое вы обнаружите в нижней части модели (той, что ближе к вам). Когда вы проделаете эти манипуляции, у вас получится вот такая замечательная форма:

Урок № 3: модульная сборка

Еще один любопытный способ, как сделать очень симпатичный параллелепипед из бумаги.

Сложите квадратный лист пополам и каждую половину еще раз вдоль надвое. Пусть два крайних сгиба «встретятся» в центре.

Переверните заготовку. Потяните левый нижний угол к середине и прогладьте линию сгиба.

Повторите то же действие, но уже с верхним правым уголком.

Верхний уголок опустите вниз, а нижний – наверх. У вас получится квадрат.

Дайте этим уголкам развернуться обратно.

Первый модуль готов.

Сделайте еще 5 таких же, но из листов другого цвета:

Соедините их в один параллелепипед. Для чего каждый острый уголок вставьте в «кармашек» соседней части кубика.

Создание модели, даже такой с детства знакомой формы, как параллелепипед, не терпит халатности. Точность в размерах, прямота линий — вот где кроется успех исполнения и удовлетворение от полученного результата.

Источники:

http://www.bolshoyvopros.ru/questions/524960-kak-sdelat-parallelepiped-iz-bumagi-shema-video-foto.html
http://ladyspecial.ru/dom-i-xobbi/svoimi-rukami/kak-sdelat-iz-bumagi-parallelepiped-i-kub
http://fb.ru/article/133903/parallelepiped-iz-bumagi-tri-tehnologii-na-odnoy-stranichke

Объемный параллелепипед из бумаги схема. Как сделать параллелепипед из бумаги своими руками поэтапно

Как сделать параллелепипед из бумаги, схема (видео, фото)?

Для того чтобы сделать параллелепипед из бумаги своими руками вам потребуется следующее:

ножницы, линейка, карандаш, лист плотной бумаги и вот эта схема.

Вырезаем из бумаги вот такую деталь и при помощи клея ПВА и кисточки склеиваем, и получаем аккуратный и ровный параллелепипед.

Параллелепипед — это объёмная геометрическая фигура, имеющая 6 граней (противоположные грани являются параллельными друг другу), каждая из них является параллелограммом.

Самый известный тип параллелепипеда — это прямоугольный параллелепипед, у него все грани являются прямоугольниками.

Форму прямоугольного параллелепипеда имеет немало вещей, с которыми мы сталкиваемся в жизни — коробка, пачка бумаги, шкаф, спичечный коробок и многие другие.

Чтобы сделать параллелепипед из бумаги, нужно воспользоваться развёртками.

Вот как выглядит развёртка прямоугольного параллелепипеда:

Её вполне можно начертить на бумаге самостоятельно с нужными вам размерами.

Главное помните, что у вас должно получится 3 пары равных по размерам прямоугольников (или 2 пары равных между собой прямоугольников для боковых граней + 2 квадрата одинаковых размеров для оснований).

Гораздо удобнее, когда на развёртке вспомогательные клапаны (это специальные полоски для соединения граней).

Вот этапы создания параллелепипеда:

1) Сначала нужно «перенести» развёртку на лист бумаги (или картона).

Проще всего будет распечатать уже готовую схему (развёртку) на принтере (увеличив его до нужных размеров).

А можно, как я сказал выше, начертить всё самим.

2) Вырезаем развёртку ножницами.

3) Теперь аккуратно сгибаем развёртку по линиям сгиба: всего будет 5 таких линий + 7 линий для вспомогательных клапанов.

4) Наконец, соединяем все грани и склеиваем их.

Также предлагаю развёртку для наклонного параллелепипеда:

На выходе получится уже несколько другая объёмная фигура, но всё делаем по тому же самому принципу, что и в случае с прямоугольным параллелепипедом (переносим развёртку — вырезаем — сгибаем — соединяем и склеиваем).

Параллелепипед бывает прямоугольный и обычный. Рассмотрим, как можно научиться делать любые параллелепипеды, то есть с любым углом.

Сначала вычерчиваем на бумаге боковую сторону параллелепипеда, то есть ту, у которой может быть острый угол (на рисунке обозначено как a). Вычерчиваем такую, какая нам нужна. Затем подкладываем под эту бумагу ещё один лист, то есть чтобы получилась двойная бумага. Легче даже сначала сложить лист бумаги пополам, а потом уже чертить. Затем вырезаем эту сторону. Так как у нас был двойной лист, то получилось сразу две одинаковых четыреугольных фигуры.

Затем на одинарной бумаге вычерчиваем выкройку b. Она должна быть с прямыми углами. Её стороны должны быть равны тем сторонам боковых поверхностей, как обозначено на рисунке. Одинаковые стороны обозначены одинаковыми линиями.

Затем обводим эту фигуру линией с отступом, чтобы начертить линию сгиба, которая будет промазываться клеем. Затем вырезаем эту фигуру, чтобы получилось как на рисунке b. Затем складываем две дальние стороны этой выкройки и склеиваем их чтобы фигура сомкнулась. Предварительно перед этим складываем все части сгибов, чтобы они стали угловатые. Затем промазываем части выкройки b, выделенные под клей. И прикладываем к обоим сторонам обе a части.

Размеры на приведённом рисунке схематичны, вообщем их не нужно выводить на принтер и использовать в качестве выкройки, так как они рисовались в Пеинте, а не по размерам.

Параллелепипед из бумаги: три технологии на одной страничке

Может оказаться немало причин, когда нужно самому сделать параллелепипед: школьное домашнее задание по выполнению модели простейшего геометрического тела, желание смастерить своими руками упаковку для подарка или даже неповторимое оформление домашнего интерьера.

При чем здесь трехмерный многоугольник?

Прямо говоря, все это под силу такой простой форме, как параллелепипед. Из бумаги его сделать проще и быстрее всего. Рассмотрим наиболее интересные варианты: склейка фигуры из выкройки по заданному чертежу, оригами и модульная сборка.

Урок № 1: объемная модель

Для того чтобы сделать прямоугольный параллелепипед из бумаги, понадобится картон, линейка, карандаш и ножницы.

Прежде всего, вы должны точно знать, какого размера модель хотите получить. На отдельном листочке запишите основные размеры параллелепипеда: высоту боковых поверхностей, длину и ширину.

Далее воспользуйтесь примером чертежа:

Важно не просто перечертить образец, а по нужным параметрам. Тогда в результате не произойдет разочарования и необходимости делать двойную работу.

Когда ваша схема будет готова, под линейку обведите полученный чертеж острием ножниц. Это необходимо сделать для того, чтобы картон в местах сгиба аккуратно складывался, а не «диктовал» свои линии.

Перед вами развернутый параллелепипед. Из бумаги своими руками вырежьте заготовку. Сложите ее с обратной стороны по обозначенным линиям.

Осталось лишь изнутри приклеить боковые припуски к прилегающим сторонам модели и ваш параллелепипед готов.

Урок № 2: Оригами

В детстве вам наверняка доводилось играть кубиками. Конечно, в то время вы не догадывались, что имеете дело с параллелепипедами. В процессе игры до параллельности всех сторон нет никакого дела, зато важны функциональные возможности. Да и не выговорить ребенку сложного слова. Главное, что восторг детства можно повторить, но уже на новом уровне. Как? Сделать параллелепипед из бумаги, воспользовавшись техникой оригами. Да не одну модель, а столько, сколько лампочек на вашей галогеновой гирлянде. Посмотрите, что в итоге у вас получится.

Возьмите квадратный лист бумаги. Согните его пополам. Разверните и еще раз сложите с другой стороны.

Повторите те же действия, только в направлении от углов.

Держите пальцами две противоположные стороны листа по центру. Две другие противолежащие поверхности тоже устремите друг к другу и пригладьте полученный треугольник, зафиксировав тем самым новые линии сгиба.

Сначала с одной стороны, а затем и с другой поднимите углы треугольника к вершине.

Получился так называемый ромб. Сведите его правый и левый углы в центре. Снова разгладьте будущий параллелепипед из бумаги.

Сделайте обратное действие. Приоткройте только что согнутые уголки и сложите другие. Они образуются из свободных концов бумажного листа и направляются вершинами к линиям сгибов в противоположные друг от друга стороны.

Все это сложно для понимания лишь до момента, пока вы не увидите, о чем, собственно, идет речь.

Вставьте только что полученные уголочки в образовавшиеся кармашки, как показано на примере.

Итак, параллелепипед из бумаги готов! Просто он пока еще в сложенном состоянии. Придать ему объема можно двумя способами. Первый: надуть. Второй: взять длинный стержень от обыкновенной шариковой ручки и воспользоваться им. Оба способа осуществляются через единственное отверстие, которое вы обнаружите в нижней части модели (той, что ближе к вам). Когда вы проделаете эти манипуляции, у вас получится вот такая замечательная форма:

Урок № 3: модульная сборка

Еще один любопытный способ, как сделать очень симпатичный параллелепипед из бумаги.

Сложите квадратный лист пополам и каждую половину еще раз вдоль надвое. Пусть два крайних сгиба «встретятся» в центре.

Переверните заготовку. Потяните левый нижний угол к середине и прогладьте линию сгиба.

Повторите то же действие, но уже с верхним правым уголком.

Верхний уголок опустите вниз, а нижний – наверх. У вас получится квадрат.

Дайте этим уголкам развернуться обратно.

Первый модуль готов.

Сделайте еще 5 таких же, но из листов другого цвета:

Соедините их в один параллелепипед. Для чего каждый острый уголок вставьте в «кармашек» соседней части кубика.

Создание модели, даже такой с детства знакомой формы, как параллелепипед, не терпит халатности. Точность в размерах, прямота линий — вот где кроется успех исполнения и удовлетворение от полученного результата.

Как сделать параллелепипед из бумаги?

Играя с ребенком различными геометрическими фигурками, вы помогаете ему развивать пространственное мышление и воображение. Он начинает понимать, что значит квадратный, круглый, кубический, шарообразный, прямоугольный и без труда сможет представить это в своей голове. Даже ученикам в школе на уроке геометрии преподаватели всегда показывают макеты различных фигур, что способствует лучшему усвоению геометрических теорем и аксиом. И, пожалуй, самое сложное и трудновыговариваемое слово для ребенка – «параллелепипед». Для того, чтобы освоить эту фигуру и понять её закономерности, предлагаем вам и вашему ребенку сделать параллелепипед из бумаги своими руками.

Для этого вам потребуется:

• плотная бумага (но не картон, иначе ребенку такая поделка доставит много трудностей), можно использовать лист из альбома;
• карандаш;
• линейка;
• ножницы;
• клей ПВА.

Чтобы понять, как делать параллелепипед из бумаги, необходимо вспомнить, как он выглядит и что из себя представляет. Эта фигура имеет 6 граней, каждая из которых является прямоугольником. Следовательно, развертка будет состоять из 6 соединенных между собой прямоугольников, находящихся в одной плоскости.

1. Как и любая объемная фигура, параллелепипед имеет длину, ширину и высоту. Именно от их значения будет зависеть размер полученной подделки. Определим желаемые величины и запишем их.

2. Приступим к начертанию схемы прямоугольного параллелепипеда на бумаге. Помните, что бумага не должна быть слишком тонкой, она легко намокнет от клея и покоробится, тогда фигурка не получится ровной, а излишне толстый картон будет плохо сгибаться и трескаться на изгибах.

3. Начертим горизонтальную линию, длина которой будет равна сумме ширины и высоты, умноженных на два. Затем из каждого конца линии опустим перпендикуляр, равный длине предполагаемого параллелограмма. Между ними проведем линию, параллельную первой.

4. Теперь от верхнего правого угла отложим высоту параллелограмма, после — ширину. Затем снова высоту, и снова ширину. От полученных точек проведем перпендикулярные линии к противоположной стороне, которые будут равны длине параллелограмма. Таким образом, мы получили 4 грани фигуры. Осталось еще 2 .

5. Над вторым прямоугольником справа дочертим ещё два снизу и сверху. В этом случае от второй отметки справа, которую мы делали в пункте 4, проведем перпендикуляр вверх равный высоте фигуры. Тоже самое повторим из второй отметки. Соединим перпендикуляры отрезком, равным ширине параллелограмма. Аналогичным методом построим нижний прямоугольник на противоположной стороне.

6. Для того, чтобы было легче склеивать параллелепипед из бумаги, добавим к чертежу дополнительные «крылышки», как указано на рисунке. Их ширина должна быть около 1.5 см. Также необходимо сделать им скошенные углы (45 градусов), чтобы при склеивании они не выглядывали наружу.

Итак, развертка параллелепипеда из бумаги готова. Важно, чтобы все детали чертежа были ровными и строго измеренными, иначе фигура не склеится ровно и будет кривой.

7. Вырежем заготовку и согнем её по всем линиям так, чтобы наши боковые грани соприкасались, а верхний и нижний прямоугольники стали «дном» и «крышкой» фигуры.

8. Смажем дополнительные «крылышки» клеем и соберем параллелепипед, заправив их внутрь. Подождем, пока клей высохнет.

Если вы освоили изготовление данной фигурки, можно приступить к собиранию наклонного параллелепипеда из бумаги, гранями которого являются остроугольные ромбы.

1. По аналогии первой фигуры, начертим схему, как показано на рисунке. Как вы видите все грани наклонного параллелепипеда одинаковы и все стороны ромбов равны между собой.
2. Добавим к рисунку дополнительные крылышки для склеивания.
3. Аккуратно соберем фигуру.

Параллелепипед — достаточно простая геометрическая фигура, освоив которую вы можете перейти к другим — создать пирамиду из картона или бумаги иди, например икосаэдр.

Источники:

http://www.bolshoyvopros.ru/questions/524960-kak-sdelat-parallelepiped-iz-bumagi-shema-video-foto.html
http://fb.ru/article/133903/parallelepiped-iz-bumagi-tri-tehnologii-na-odnoy-stranichke
http://womanadvice.ru/kak-sdelat-parallelepiped-iz-bumagi

Как сделать параллелепипед из картона своими руками. Как сделать параллелепипед из бумаги схема

Параллелепипеды нас окружают ежедневно, они везде вокруг нас. Из параллелепипедов состоит большая часть сооружений, разные ящики и коробочки, и кирпичи, и кусочки рафинада.

Эта форма положена в основу в машиностроении. В быту дома нас сплошь и рядом окружают параллелепипеды мебели!

А давайте попробуем сделать их своими руками из бумаги? Поэтапный ход работы прилагается ниже.

Читайте также:

Изготовление параллелепипеда из бумаги

Пошаговая инструкция:

1. Нам понадобится альбомный лист бумаги или картона.
Для изготовления больших демонстрационных моделей параллелепипеда используют картон. Они создаются путем склеивания из заранее подготовленной заготовки.

Маленькие модельки, в большинстве случаев, изготавливают из плотной бумаги.

Нужно взять лист картона и при помощи линейки и карандаша начертить развертку модели параллелепипеда необходимого вам размера.

2. Наносить чертеж
развертки необходимо таким образом, чтобы процесс изготовления происходил как можно легче. Самый оптимальный вариант – чтобы склеивать самую длинную сторону всего лишь один раз.

Главное — не забыть про боковые стороны
. Их нужно нарисовать с каждой стороны по одной.

Необходимо скурпулезно проверить все размеры, углы. Чтобы при склеивании параллелепипеда не получилось перекосов и ваша модель была правильной формы. При нанесении развертки на бумаги все сгибы необходимо наносить пунктирной линией.

3. Во время нанесения чертежа развертки на бумагу самое главное не забыть о припусках для склеивания. Припуски, в большинстве случаев, необходимо делать не менее 1 см. Уголочки припусков необходимо срезать до самого рисунка под углом около 45 градусов.

Это необходимо для того, чтобы они не создавали дискомфорта при склеивании модели. Если ваша модель будет из обычной бумаги – нужно просто вырезать ее по нанесенному контуру из бумаги и сделать сгибы в обозначенных местах.

Если же ваша модель будет изготавливаться из картона – здесь все немного сложнее. Так же вырезаем по контуру развертки наш параллелепипед и в местах, предназначенных для сгиба, необходимо слегка под линейку надрезать картон ножом и загнуть в обратную стор

Как сделать параллелепипед из бумаги схема

Распечатать
Спасибо, отличный урок +15

Чаще всего для создания геометрических фигур используют квадрат и конус. Их делать намного проще и быстрее. А вот чтобы сделать своими руками параллелепипед из бумаги – потребуется немного попотеть, ведь он имеет стороны с разными цифровыми значениями.

Необходимые материалы для параллелепипеда

• Лист бумаги
• Ножницы
• Линейка
• Карандаш
• Клей

Как сделать параллелепипед из бумаги поэтапно

Для начала потребуется выбрать подходящую бумагу. Если вы просто хотите научиться делать параллелепипед своими руками, то можете взять обычную белую бумагу. Однако, она прослужит вам не долго. Так что лучше подберите полукартон любимого цвета.

Также важную роль будет играть формат листа, ведь от него будет зависеть размер готового параллелепипеда. Для маленькой геометрической фигуры подойдет А4, но если желаете сделать побольше, то возьмите А3 или даже А2.

Подобрав бумагу переходим к прорисовке. Для этого берем линейку и простой карандаш. На всякий случай следует иметь ластик.

Вырезаем по контуру. Так как это не квадрат, то стороны будут разными: где-то шире, а где-то уже. Не забудьте вырезать небольшие боковые стороны для склейки фигуры.

Сгибаем все линии вовнутрь. Имея под рукой канцелярский нож и железную линейку можно провести по всем карандашным линиям небольшие надрезы. Делать это следует аккуратно, чтобы не разрезать бумагу. Надрезы должны доходить не более, чем до половины общей толщины.

Начинаем склеивать стороны.

Далее проклеим с правой стороны.

Напоследок нанесем капельки клея на боковые стороны и склеим левую сторону.

Вот теперь можно с уверенностью сказать, что параллелепипед из бумаги готов. Его можно использовать, как в учебных целях, так и для игр.

три технологии на одной страничке

Параллелепипед – объемная геометрическая фигура, в основании которой лежит многоугольник, а грани являются параллелограммами. Многим школьникам сложно осмыслить это понятие и тем более решать задачи на вычисление площади и объема параллелепипеда. Для того чтобы помочь ребенку в освоении знаний по геометрии, сделайте вместе с ним из бумаги макет фигуры.

Как сделать параллелепипед из белой бумаги

Объемная модель собирается из трафарета, который просто сделать самим. Приготовьте: лист бумаги А4, карандаш, линейку, ножницы, клей.

• Положите лист перед собой широкой стороной (вдоль). Разделите с 2-х сторон его боковую часть, равную 21 см, пополам и проведите линию.
• Допустим, что высота ребра параллелепипеда – 10 см. Отмерьте от середины с двух краев вверх и вниз по 5 см и соедините отметки отрезками.
• Для образования сторон фигуры, отложите на первой и последней линиях поочередно – 8, 5, 8, 5 см. Соедините линии по точкам между собой – получились ребра параллелепипеда.
• На второй и третьей вертикальных прямых отметьте от их начала и конца (вверх и вниз) по 5 см, так как у нас ширина одной стороны 5 см и соедините концы отрезков, получив четырехугольник.
• Отступите от контура фигуры по 1,5 см с каждой стороны и проведите наметку, которая обозначит места для крепления.

Важно: не заходите за выступающие боковые прямоугольники, чтобы впоследствии случайно их не порезать.

• Вырежьте получившуюся фигуру, срежьте уголками кончики полосок для склеивания.
• Согните заготовку по краям, промяв их руками. Переложите основу на другую сторону, чтобы карандашная сетка осталась внутри, и продавите наметку по всей поверхности.
• Намажьте клеем припуск на одной боковой стороне. Сверните фигуру и, начиная с крайней полоски, приклейте к ней противоположную грань, затем – верхнее основание. Повторите процедуру с другой стороны и параллелепипед готов.

Как сделать прямоугольный параллелепипед из бумаги – куб

Куб – тоже параллелепипед, только прямоугольный, грани которого – квадраты. Вычерчивается он по такой же схеме, как в первом варианте.

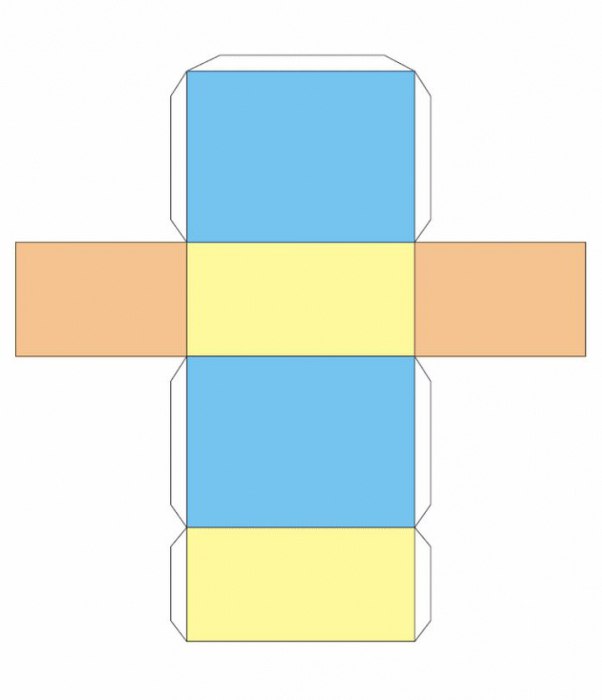
• Постройте последовательно четыре квадрата горизонтального направления и два – по бокам второго по вертикальной оси. Пририсуйте клапаны на склейку.

• Вырежьте развертку, промните грани, намажьте клеем припуски и склейте куб.

Как сделать параллелепипед из бумаги в технике оригами

Этот способ хорош тем, что для изготовления фигуры нужен лишь квадратный лист бумаги.

• Согните лист напополам с двух сторон, получившиеся углы поделите надвое, чтобы вышла заготовка из сложенных треугольников.

• Переверните фигуру на 90º. Загните слева и справа уголки до соприкосновения, продавив сгибы пальцами. Положите лист обратной стороной, повторите действия.

• Отверните согнутые углы и сложите другие, образованные из свободных кончиков листа и направленных вершинами к сгибам.

• Вставьте уголки в получившиеся кармашки.

• В отверстие, образовавшееся в нижней части модели, вставьте карандаш или дуньте, и фигура обретет объем.

Бумажный параллелепипед можно использовать не только как наглядное пособие по геометрии. Если фигурки сделать из цветного картона, они пригодятся в детских играх, а выполненные из декоративной бумаги – помогут красиво упаковать подарок или сувенир.

Играя с ребенком различными геометрическими фигурками, вы помогаете ему развивать пространственное мышление и воображение. Он начинает понимать, что значит квадратный, круглый, кубический, шарообразный, прямоугольный и без труда сможет представить это в своей голове. Даже ученикам в школе на уроке геометрии преподаватели всегда показывают макеты различных фигур, что способствует лучшему усвоению геометрических теорем и аксиом. И, пожалуй, самое сложное и трудновыговариваемое слово для ребенка – «параллелепипед». Для того, чтобы освоить эту фигуру и понять её закономерности, предлагаем вам и вашему ребенку сделать параллелепипед из бумаги своими руками.

Для этого вам потребуется:

• плотная бумага (но не картон, иначе ребенку такая поделка доставит много трудностей), можно использовать лист из альбома;
• карандаш;
• линейка;
• ножницы;
• клей ПВА.

Чтобы понять, как делать параллелепипед из бумаги, необходимо вспомнить, как он выгляди

три технологии на одной страничке

Может оказаться немало причин, когда нужно самому сделать параллелепипед: школьное домашнее задание по выполнению модели простейшего геометрического тела, желание смастерить своими руками упаковку для подарка или даже неповторимое оформление домашнего интерьера.

При чем здесь трехмерный многоугольник?

Прямо говоря, все это под силу такой простой форме, как параллелепипед. Из бумаги его сделать проще и быстрее всего. Рассмотрим наиболее интересные варианты: склейка фигуры из выкройки по заданному чертежу, оригами и модульная сборка.

Урок № 1: объемная модель

Для того чтобы сделать прямоугольный параллелепипед из бумаги, понадобится картон, линейка, карандаш и ножницы.

Прежде всего, вы должны точно знать, какого размера модель хотите получить. На отдельном листочке запишите основные размеры параллелепипеда: высоту боковых поверхностей, длину и ширину.

Далее воспользуйтесь примером чертежа:

Важно не просто перечертить образец, а по нужным параметрам. Тогда в результате не произойдет разочарования и необходимости делать двойную работу.

Когда ваша схема будет готова, под линейку обведите полученный чертеж острием ножниц. Это необходимо сделать для того, чтобы картон в местах сгиба аккуратно складывался, а не «диктовал» свои линии.

Перед вами развернутый параллелепипед. Из бумаги своими руками вырежьте заготовку. Сложите ее с обратной стороны по обозначенным линиям.

Осталось лишь изнутри приклеить боковые припуски к прилегающим сторонам модели и ваш параллелепипед готов.

Урок № 2: Оригами

В детстве вам наверняка доводилось играть кубиками. Конечно, в то время вы не догадывались, что имеете дело с параллелепипедами. В процессе игры до параллельности всех сторон нет никакого дела, зато важны функциональные возможности. Да и не выговорить ребенку сложного слова. Главное, что восторг детства можно повторить, но уже на новом уровне. Как? Сделать параллелепипед из бумаги, воспользовавшись техникой оригами. Да не одну модель, а столько, сколько лампочек на вашей галогеновой гирлянде. Посмотрите, что в итоге у вас получится.

Шаг 1

Возьмите квадратный лист бумаги. Согните его пополам. Разверните и еще раз сложите с другой стороны.

Шаг 2

Повторите те же действия, только в направлении от углов.

Шаг 3

Держите пальцами две противоположные стороны листа по центру. Две другие противолежащие поверхности тоже устремите друг к другу и пригладьте полученный треугольник, зафиксировав тем самым новые линии сгиба.

Шаг 4

Сначала с одной стороны, а затем и с другой поднимите углы треугольника к вершине.

Шаг 5

Получился так называемый ромб. Сведите его правый и левый углы в центре. Снова разгладьте будущий параллелепипед из бумаги.

Не забудьте перевернуть и загнуть уголки с обратной стороны.

Шаг 6

Сделайте обратное действие. Приоткройте только что согнутые уголки и сложите другие. Они образуются из свободных концов бумажного листа и направляются вершинами к линиям сгибов в противоположные друг от друга стороны.

Все это сложно для понимания лишь до момента, пока вы не увидите, о чем, собственно, идет речь.

Шаг 7

Вставьте только что полученные уголочки в образовавшиеся кармашки, как показано на примере.

Шаг 8

Итак, параллелепипед из бумаги готов! Просто он пока еще в сложенном состоянии. Придать ему объема можно двумя способами. Первый: надуть. Второй: взять длинный стержень от обыкновенной шариковой ручки и воспользоваться им. Оба способа осуществляются через единственное отверстие, которое вы обнаружите в нижней части модели (той, что ближе к вам). Когда вы проделаете эти манипуляции, у вас получится вот такая замечательная форма:

В то же отверстие, через которое кубик надувался, вставляется и галогеновая лампочка.

Урок № 3: модульная сборка

Еще один любопытный способ, как сделать очень симпатичный параллелепипед из бумаги.

Шаг 1

Сложите квадратный лист пополам и каждую половину еще раз вдоль надвое. Пусть два крайних сгиба «встретятся» в центре.

Шаг 2

Переверните заготовку. Потяните левый нижний угол к середине и прогладьте линию сгиба.

Шаг 3

Повторите то же действие, но уже с верхним правым уголком.

Шаг 4

Верхний уголок опустите вниз, а нижний – наверх. У вас получится квадрат.

Шаг 5

Дайте этим уголкам развернуться обратно.

Первый модуль готов.

Шаг 6

Сделайте еще 5 таких же, но из листов другого цвета:

Шаг 7

Соедините их в один параллелепипед. Для чего каждый острый уголок вставьте в «кармашек» соседней части кубика.

Совет

Создание модели, даже такой с детства знакомой формы, как параллелепипед, не терпит халатности. Точность в размерах, прямота линий — вот где кроется успех исполнения и удовлетворение от полученного результата.

Как сделать параллелепипед из бумаги?

Играя с ребенком различными геометрическими фигурками, вы помогаете ему развивать пространственное мышление и воображение. Он начинает понимать, что значит квадратный, круглый, кубический, шарообразный, прямоугольный и без труда сможет представить это в своей голове. Даже ученикам в школе на уроке геометрии преподаватели всегда показывают макеты различных фигур, что способствует лучшему усвоению геометрических теорем и аксиом. И, пожалуй, самое сложное и трудновыговариваемое слово для ребенка – «параллелепипед». Для того, чтобы освоить эту фигуру и понять её закономерности, предлагаем вам и вашему ребенку сделать параллелепипед из бумаги своими руками.

Для этого вам потребуется:

• плотная бумага (но не картон, иначе ребенку такая поделка доставит много трудностей), можно использовать лист из альбома;
• карандаш;
• линейка;
• ножницы;
• клей ПВА.

Чтобы понять, как делать параллелепипед из бумаги, необходимо вспомнить, как он выглядит и что из себя представляет. Эта фигура имеет 6 граней, каждая из которых является прямоугольником. Следовательно, развертка будет состоять из 6 соединенных между собой прямоугольников, находящихся в одной плоскости.

1. Как и любая объемная фигура, параллелепипед имеет длину, ширину и высоту. Именно от их значения будет зависеть размер полученной подделки. Определим желаемые величины и запишем их.

2. Приступим к начертанию схемы прямоугольного параллелепипеда на бумаге. Помните, что бумага не должна быть слишком тонкой, она легко намокнет от клея и покоробится, тогда фигурка не получится ровной, а излишне толстый картон будет плохо сгибаться и трескаться на изгибах.

3. Начертим горизонтальную линию, длина которой будет равна сумме ширины и высоты, умноженных на два. Затем из каждого конца линии опустим перпендикуляр, равный длине предполагаемого параллелограмма. Между ними проведем линию, параллельную первой.

4. Теперь от верхнего правого угла отложим высоту параллелограмма, после — ширину. Затем снова высоту, и снова ширину. От полученных точек проведем перпендикулярные линии к противоположной стороне, которые будут равны длине параллелограмма. Таким образом, мы получили 4 грани фигуры. Осталось еще 2 .

5. Над вторым прямоугольником справа дочертим ещё два снизу и сверху. В этом случае от второй отметки справа, которую мы делали в пункте 4, проведем перпендикуляр вверх равный высоте фигуры. Тоже самое повторим из второй отметки. Соединим перпендикуляры отрезком, равным ширине параллелограмма. Аналогичным методом построим нижний прямоугольник на противоположной стороне.

6. Для того, чтобы было легче склеивать параллелепипед из бумаги, добавим к чертежу дополнительные «крылышки», как указано на рисунке. Их ширина должна быть около 1.5 см. Также необходимо сделать им скошенные углы (45 градусов), чтобы при склеивании они не выглядывали наружу.

Итак, развертка параллелепипеда из бумаги готова. Важно, чтобы все детали чертежа были ровными и строго измеренными, иначе фигура не склеится ровно и будет кривой.

7. Вырежем заготовку и согнем её по всем линиям так, чтобы наши боковые грани соприкасались, а верхний и нижний прямоугольники стали «дном» и «крышкой» фигуры.

8. Смажем дополнительные «крылышки» клеем и соберем параллелепипед, заправив их внутрь. Подождем, пока клей высохнет.

Если вы освоили изготовление данной фигурки, можно приступить к собиранию наклонного параллелепипеда из бумаги, гранями которого являются остроугольные ромбы.

1. По аналогии первой фигуры, начертим схему, как показано на рисунке. Как вы видите все грани наклонного параллелепипеда одинаковы и все стороны ромбов равны между собой.



2. Добавим к рисунку дополнительные крылышки для склеивания.
3. Аккуратно соберем фигуру.

Параллелепипед — достаточно простая геометрическая фигура, освоив которую вы можете перейти к другим — создать пирамиду из картона или бумаги иди, например икосаэдр.

 

изображений, фотографий и векторов параллелепипеда

В настоящее время вы используете старую версию браузера, и ваш опыт работы может быть неоптимальным. Пожалуйста, подумайте об обновлении. Выучить больше. ImagesImages homeCurated collectionsPhotosVectorsOffset ImagesCategoriesAbstractAnimals / WildlifeThe ArtsBackgrounds / TexturesBeauty / FashionBuildings / LandmarksBusiness / FinanceCelebritiesEditorialEducationFood и DrinkHealthcare / MedicalHolidaysIllustrations / Clip-ArtIndustrialInteriorsMiscellaneousNatureObjectsParks / OutdoorPeopleReligionScienceSigns / SymbolsSports / RecreationTechnologyTransportationVectorsVintageAll categoriesFootageFootage homeCurated collectionsShutterstock SelectShutterstock ElementsCategoriesAnimals / WildlifeBuildings / LandmarksBackgrounds / TexturesBusiness / FinanceEducationFood и DrinkHealth CareHolidaysObjectsIndustrialArtNaturePeopleReligionScienceTechnologySigns / SymbolsSports / RecreationTransportationEditorialAll categoriesEditorialEditorial ГлавнаяРазвлеченияНовостиРоялтиСпортМузыкаМузыка домойПремиумBeatИнструментыShutterstock EditorМобильные приложенияПлагиныИзменение размера изображенияКонвертер файловСоздатель коллажейЦветовые схемыБлог Главная страница блогаДизайнВидеоКонтроллерНовости

---

PremiumBeat blogEnterprisePric ing

Войти

Зарегистрироваться

Меню

ФильтрыВсе изображения

• Все изображения
• Фото
• Векторы
• Иллюстрации
• Редакционные
• Видеоряд
• Музыка

---

• Поиск по изображению

параллелепипед

Поиск изображение

• Сортировать по

• Самое актуальное

  Свежий контент

• Тип изображения

• Все изображения

  Фото

,

Simple English Wikipedia, бесплатная энциклопедия

В геометрии параллелепипед — это трехмерная фигура, образованная шестью параллелограммами (термин ромбовидный также иногда используется в этом значении). По аналогии, он относится к параллелограмму так же, как куб относится к квадрату или как кубоид к прямоугольнику. В евклидовой геометрии его определение включает в себя все четыре понятия (т.е. параллелепипед , параллелограмм , куб и квадрат ).В контексте аффинной геометрии, в которой углы не различаются, ее определение допускает только параллелограммов и параллелепипедов . Три эквивалентных определения параллелепипеда :

Прямоугольный кубоид (шесть прямоугольных граней), куб (шесть квадратных граней) и ромбоэдр (шесть граней ромба) — все это частные случаи параллелепипеда.

Любая из трех пар параллельных граней может рассматриваться как базовая плоскость призмы.У параллелепипеда три набора из четырех параллельных ребер; края в каждом наборе имеют одинаковую длину.

Параллелепипеды возникают в результате линейных преобразований куба (для невырожденных случаев: биективные линейные преобразования).

Поскольку каждая грань имеет точечную симметрию, параллелепипед является зоноэдром. Также весь параллелепипед имеет точечную симметрию C _i (см. Также триклиническую схему). Каждое лицо, если смотреть снаружи, является зеркальным отражением противоположного лица.Грани в целом хиральные, а параллелепипед — нет.

Можно заполнить мозаику конгруэнтными копиями любого параллелепипеда.

Векторы, определяющие параллелепипед.

Объем параллелепипеда равен произведению площади его основания A и высоты h . Основание — это любая из шести граней параллелепипеда. Высота — это расстояние по перпендикуляру между основанием и противоположной гранью.

Альтернативный метод определяет векторы a = ( a ₁ , a ₂ , a ₃ ), b = ( b ₁ , b ₂ , b ₃ ) и c = ( c ₁ , c ₂ , c ₃ ) для представления трех ребер, которые пересекаются в одной вершине.Тогда объем параллелепипеда равен абсолютному значению скалярного тройного произведения a · ( b × c ):

V = | a⋅ (b × c) | = | b⋅ (c × a) | = | c⋅ (a × b) | {\ displaystyle V = \ left | \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) \ right | = \ left | \ mathbf {b} \ cdot (\ mathbf {c} \ times \ mathbf {a}) \ right | = \ left | \ mathbf { c} \ cdot (\ mathbf {a} \ times \ mathbf {b}) \ right |}

Это верно, потому что, если мы выберем b и c для представления краев основания, площадь основы есть, по определению перекрестного произведения (см. геометрическое значение перекрестного произведения),

A = | b || c | sin⁡θ = | b × c |, {\ displaystyle A = \ left | \ mathbf {b} \ right | \ left | \ mathbf {c} \ right | \ sin \ theta = \ left | \ mathbf {b} \ times \ mathbf {c} \ right |,}

, где θ — это угол между b и c , а высота равна

h = | a | cos⁡α, {\ displaystyle h = \ left | \ mathbf {a} \ right | \ cos \ alpha,}

, где α — внутренний угол между a и h .

Из рисунка мы можем сделать вывод, что величина α ограничена до 0 ° ≤ α <90 °. Напротив, вектор b × c может образовывать с a внутренний угол β больше 90 ° (0 ° ≤ β ≤ 180 °). А именно, поскольку b × c параллельно h , значение β равно β = α или β = 180 ° — α . Так

cos⁡α = ± cos⁡β = | cos⁡β |, {\ displaystyle \ cos \ alpha = \ pm \ cos \ beta = \ left | \ cos \ beta \ right |,}

и

h = | a || cos⁡β |.{\ displaystyle h = \ left | \ mathbf {a} \ right | \ left | \ cos \ beta \ right |.}

Мы заключаем, что

V = Ah = | a || b × c || cos⁡β |, {\ displaystyle V = Ah = \ left | \ mathbf {a} \ right | \ left | \ mathbf {b} \ times \ mathbf {c} \ right | \ left | \ cos \ beta \ right |,}

, что, по определению скалярного (или точечного) произведения, эквивалентно абсолютному значению a · ( b × c ), QED

Последнее выражение также эквивалентно абсолютному значению определителя трехмерной матрицы, построенной с использованием a , b и c в качестве строк (или столбцов):

V = | det [a1a2a3b1b2b3c1c2c3] |.{\ displaystyle V = \ left | \ det {\ begin {bmatrix} a_ {1} & a_ {2} & a_ {3} \\ b_ {1} & b_ {2} & b_ {3} \\ c_ {1} & c_ { 2} & c_ {3} \ end {bmatrix}} \ right |.}

Это найдено с помощью правила Крамера на трех сокращенных двумерных матрицах, найденных из оригинала.

Если a , b и c — длины ребер параллелепипеда, а α, β и γ — внутренние углы между ребрами, объем равен

V = abc1 + 2cos⁡ (α) cos⁡ (β) cos⁡ (γ) −cos2⁡ (α) −cos2⁡ (β) −cos2⁡ (γ).{2} (\ gamma) \,}}.}

Соответствующий тетраэдр [изменить | изменить источник]

Объем любого тетраэдра, который имеет три сходящихся ребра параллелепипеда, имеет объем, равный одной шестой объема этого параллелепипеда (см. Доказательство).

Прямоугольный параллелепипед

Для параллелепипедов с плоскостью симметрии возможны два случая:

• имеет четыре прямоугольных грани
• он имеет две ромбические грани, в то время как из остальных граней две смежные грани равны, а две другие также (две пары являются зеркальным отображением друг друга).

См. Также моноклинический.

Прямоугольный кубоид, также называемый прямоугольным параллелепипедом или иногда просто кубоидом , представляет собой параллелепипед, все грани которого прямоугольные; куб — это кубоид с квадратными гранями.

Ромбоэдр — это параллелепипед со всеми ромбическими гранями; треугольный трапецоэдр — это ромбоэдр с совпадающими ромбическими гранями.

Идеальный параллелепипед — это параллелепипед с ребрами целой длины, диагоналями граней и диагоналями пространства.В 2009 году было показано, что существуют десятки идеальных параллелепипедов, ^[1] — ответ на открытый вопрос Ричарда Гая. В одном примере есть края 271, 106 и 103, второстепенные диагонали лица 101, 266 и 255, диагонали основной грани 183, 312 и 323 и диагонали пространства 374, 300, 278 и 272.

Известны идеальные параллелепипеды с двумя прямоугольными гранями. Но неизвестно, существуют ли такие, у которых все грани прямоугольные; такой случай можно было бы назвать идеальным кубоидом.

Коксетер назвал обобщение параллелепипеда в высших измерениях параллелоэдром .

Конкретно в n -мерном пространстве он называется n -мерным параллелотопом, или просто n -параллелоэдром. Таким образом, параллелограмм — это 2-параллелоэдр, а параллелепипед — это 3-параллелоэдр.

В более общем смысле, параллелоэдр ^[2] или вороной параллелоэдр имеет параллельные и конгруэнтные противоположные грани. Итак, 2-параллелоэдр — это параллелогон, который также может включать в себя определенные шестиугольники, а 3-параллелоэдр — это параллелоэдр, включающий 5 типов многогранников.

Диагонали параллелоэдра n пересекаются в одной точке и делятся на нее пополам. Инверсия в этой точке оставляет без изменений n -параллелоэдр. См. Также неподвижные точки групп изометрий в евклидовом пространстве.

Ребра, выходящие из одной вершины параллелоэдра k , образуют рамку k (v1,…, vn) {\ displaystyle (v_ {1}, \ ldots, v_ {n})} вектора пространство, а параллелоэдр можно восстановить из этих векторов, взяв линейные комбинации векторов с весами от 0 до 1.{m}}, где m≥n {\ displaystyle m \ geq n} может быть вычислено с помощью определителя Грама. В качестве альтернативы объем — это норма внешнего произведения векторов:

V = ‖v1∧ ⋯ ∧vn‖. {\ Displaystyle V = \ left \ | v_ {1} \ wedge \ cdots \ wedge v_ {n} \ right \ |.}

Если m = n , это составляет абсолютное значение определителя n векторов.

Другая формула для вычисления объема n -параллелоэдра P в Rn {\ displaystyle \ mathbb {R} ^ {n}}, чьи n + 1 вершины — это V0, V1,…, Vn { \ Displaystyle V_ {0}, V_ {1}, \ ldots, V_ {n}} — это

Vol (P) = | det ([V0 1] T, [V1 1] T,…, [Vn 1] T) |, {\ displaystyle {\ rm {Vol}} (P) = | {\ rm {det}} \ ([V_ {0} \ 1] ^ {\ rm {T}}, [V_ {1} \ 1] ^ {\ rm {T}}, \ ldots, [V_ {n} \ 1 ] ^ {\ rm {T}}) |,}

где [Vi 1] {\ displaystyle [V_ {i} \ 1]} — вектор-строка, образованный конкатенацией Vi {\ displaystyle V_ {i} } и 1.Действительно, определитель не изменяется, если [V0 1] {\ displaystyle [V_ {0} \ 1]} вычитается из [Vi 1] {\ displaystyle [V_ {i} \ 1]} ( i > 0), а размещение [V0 1] {\ displaystyle [V_ {0} \ 1]} в последней позиции только меняет его знак.

Точно так же объем любого n -симплекса, который имеет n сходящихся ребер параллелоэдра, имеет объем, равный единице 1/ n ! объема этого параллелоэдра.

Слово появляется как parallelipiped на в переводе сэра Генри Биллингсли «Элементов» Евклида, датированном 1570 годом.В издании 1644 года своей книги Cursus mathematicus Пьер Эригон использовал написание parallelepipedum . Оксфордский словарь английского языка цитирует современный параллелепипед как первое упоминание в книге Уолтера Чарлтона Chorea gigantum (1663).

Словарь Чарльза Хаттона (1795) показывает параллелепипедов и параллелепипедов , демонстрируя влияние объединяющей формы параллело-, как если бы вторым элементом был трубопровод , а не эпипедон .Ной Вебстер (1806) включает в себя написание параллелепипед . Оксфордский словарь английского языка издания 1989 г. описывает параллелепипедов (и параллелепипедов ) явно как неправильные формы, но они перечислены без комментариев в издании 2004 г. и только произношения с акцентом на пятом слоге pi ( / paɪ /) даны.

Отказ от традиционного произношения скрыл различное разделение, предложенное греческими корнями, с epi- («вкл») и pedon («земля»), которые в результате дают epiped , плоскую плоскость. ».Таким образом, грани параллелепипеда плоские, а противоположные грани параллельны.

• Coxeter, H. S. M. Regular Polytopes , 3-е изд. Нью-Йорк: Довер, стр. 122, 1973 г. (Он определяет параллелоэдр как обобщение параллелограмма и параллелепипеда в n-мерном пространстве.)

,

Контролируемая классификация изображений с использованием алгоритма параллелепипеда

Опубликовано 18 апреля 2017 г. | 2 | 5327

Предыдущий пост был посвящен выбору правильного метода контролируемой классификации. И на этот раз мы рассмотрим, как выполнять контролируемую классификацию в ENVI. Мы возьмем в качестве примера классификацию параллелепипедов, поскольку это самый простой алгоритм с математической точки зрения.В ENVI работа с любым другим типом контролируемой классификации очень похожа на ту, которую мы рассмотрим здесь. Интерфейс процедуры классификации практически одинаков для всех алгоритмов. Единственное, что отличает — это параметр, задающий чувствительность процедуры. Таким образом, если пользователь научится выполнять классификацию параллелепипеда, он может легко использовать ENVI для других алгоритмов классификации.

Теория

Для начала немного теории.Для наглядности мы возьмем самый простой случай — двумерное спектральное пространство признаков (рисунок 1). Здесь нам нужно различать несколько классов. На изображении мы видим три облака точек, которые представляют три класса. Эти облака не перекрываются. Это как раз тот случай, когда нужно использовать алгоритм классификации параллелепипедов.

Рис. 1. Гипотетический пример того, когда классификация параллелепипедов является наилучшей

Для выполнения классификации параллелепипедов программе требуются два параметра для каждого из классов.Это среднее значение яркости и стандартное отклонение от среднего по всем каналам изображения.

В нашем гипотетическом примере на рисунке 1 у нас есть два канала, поэтому пространство спектральных признаков является двумерным. Оба параметра, необходимые для классификации, рассчитываются программой на основе обучающих выборок, созданных пользователем.

Процесс классификации состоит из трех этапов (рис. 2). На первом этапе алгоритм устанавливает центры для каждого класса в пространстве спектральных признаков.Поэтому необходимо знать среднюю яркость классов по всем каналам изображения. На рис. 2А показаны центры трех классов, отмеченные красными, синими и зелеными точками.

Далее алгоритм находит крайние точки каждого класса. Для этого линии прокладываются от центров классов параллельно осям пространств признаков. Их длина равна нескольким стандартным отклонениям. Точное значение задается пользователем, и эта настройка влияет на чувствительность классификации. Эта сумма может быть одинаковой для всех классов, но также может отличаться.

На рис. 2В показан второй этап классификации. 3 стандартных отклонения заложены для красного класса и 4 стандартных отклонения для зеленого и синего классов.

Рисунок 2. Этапы классификации

На завершающем этапе (рис. 2С) алгоритм строит линии, охватывающие облака точек, параллельные осям, пересекающие точки экстремумов. Все значения, которые находятся внутри, относятся к соответствующему классу. На рисунке 2 мы видим, что геометрическая форма, ограничивающая класс, представляет собой параллелепипед.Отсюда и название алгоритма. В трехмерных спектральных классах будет ограничиваться параллелограммом. Если на изображении более трех каналов, фигура представляет собой так называемый гиперпараллелепипед.

Практика

Попрактикуемся в классификации на старом примере. Это часть изображения со спутника Landsat 5 TM, сделанного 16 сентября 2009 г. (рис. 3). В районе реки Северский Донец в районе Мохнача нам потребуется выделить три класса объектов: лиственные леса, хвойные леса и водоемы.

Рис. 3. Изображение Landsat (слева) и тренировочные районы (справа)

1) Все процедуры контролируемой классификации начинаются с создания обучающей выборки. Это часть процесса надзора. В ENVI это реализовано путем создания регионов интереса (ROI). У каждого класса свой набор областей интереса. Что нужно сделать дальше, так это проверить качество выбранных регионов интереса (подробнее об этом см. Этот пост).

2) Используя n-D Vizualizer, просмотрите расположение облаков точек вашего класса в пространстве объектов (читайте об этом здесь). Если они не пересекаются, то можно использовать метод классификации параллелепипедов.

3) После создания обучающих наборов можно начинать процедуру классификации. Для этого выберите Classification → Supervised Classification → Parallelepiped Classification в Toolbox . Окно входного файла классификации откроет . Выберите изображение, которое необходимо классифицировать.

4) После выбора изображения появится другое окно — Parallelepiped Parameters . В этом окне необходимо задать параметры классификации. Есть четыре настройки, которые соответствуют разным разделам окна ( Parallelepiped Parameters) :

• Выберите классы из регионов
• Установить максимальное стандартное отклонение от среднего
• Результат вывода на
• Изображения правил вывода

Рисунок 4. Параметры параллелепипеда окно

5) Список интересующих регионов состоит из всех областей интереса, которые были созданы во время текущего сеанса ENVI. Но мы можем использовать только некоторые из них для обучения. Итак, по умолчанию ни одна из областей интереса не выбрана, выберите те, которые хотите использовать, щелкнув левой кнопкой мыши. Если необходимо выбрать все регионы, нажмите кнопку Select All Items . Очистить все элементы кнопка отменяет выбор.

6) Установите максимальное стандартное отклонение от среднего.ENVI имеет три различных настройки для этого индикатора: Нет, Одно значение, Несколько значений . Примеры результатов для этих вариантов показаны на рисунке 5.

Рисунок 5. Результаты классификации для различных настроек стандартного отклонения от среднего. A — Нет, B — Одно значение (стандартное отклонение равно 3), C — Одно значение (стандартное отклонение равно 4), D — Несколько значений (стандартное отклонение для водоемов составляет 3,5, лиственных лесов — 5.0, для хвойных лесов — 6,0)

A) Если вы выберете Нет , будет использоваться нулевое значение. В данный момент вход не требуется. Процедура классификации будет искать только те пиксели, которые строго равны среднему классу, установленному в ROI. Как правило, при использовании этого параметра значения для областей классов будут очень маленькими (рис. 5A).

B) Значение по умолчанию — Single Value — одинаковое значение для всех классов. Этот вариант лучше всего подходит, когда облака точек значений имеют одинаковые размеры в многомерном пространстве объектов.Если они действительно различаются по размеру, в некоторых случаях все еще можно использовать то же самое значение максимального отклонения от среднего. Это тот случай, когда расстояние между облаками достаточно велико. Таким образом, параллелепипеды, определяемые размером самого большого облака, не перекрывают друг друга.
В опции Single Value по умолчанию максимальное стандартное отклонение от среднего установлено на 3,00. Вы можете указать другое значение, подходящее для вашего случая. Если значение ниже оптимального, классы площадей будут меньше реальных, поэтому будут ошибки пропуска.Мы видим на рисунке 5B, где в лесах есть участки с белыми пятнами. Если значение выше оптимального, классы площадей будут завышены, поэтому возникнут ошибки коммиссии. Пример этого можно увидеть на Рисунке 5C, где классифицируется гораздо больше воды, чем на самом деле в этом районе.

C) В случае, если облака точек класса имеют разные размеры (диаметры) в пространстве спектральных характеристик, тогда следует использовать опцию Multiple Values ​​ . Если вы установите переключатель на эту опцию, появится кнопка Назначить несколько значений .Нажмите ее, чтобы открыть Assign Max stdv из окна Mean , в нем содержится список областей интереса и поле ввода значения ( Edit Select Item: ).

Выберите каждую область интереса и установите максимальное значение стандартного отклонения.

Рисунок 6. Установка стандартного отклонения для каждого класса

7) Задайте параметры сохранения результатов классификации. Они могут быть временными (память) и постоянными (файл).

8) Установите параметры сохранения изображений правила вывода.Мы не будем сейчас рассматривать образы правил. Вкратце, это изображения областей классов при различных значениях параметров классификации (стандартное отклонение в случае алгоритма параллелепипеда). Изображения правил используются для так называемой классификации на основе правил и для создания ROC-кривых. Об этих процедурах будут отдельные посты. Если вы не планируете выполнять эту классификацию, нет необходимости сохранять образы правил. Выберите Нет ( Да установлено по умолчанию). Подобно результатам классификации, изображения правил вывода могут быть временными и храниться в файле.

9) После завершения настроек нажмите OK , и вы сразу получите результаты классификации. Но если значения стандартного отклонения были установлены неправильно, результаты классификации будут неудовлетворительными. Вот почему в ENVI есть опция предварительного просмотра результатов. Для этого нажмите кнопку Preview (рисунок 7). Окно параметров параллелепипеда будет расширено и теперь будет иметь раздел Предварительный просмотр классификации .

Рисунок 7.Предварительный просмотр результатов классификации

10) По умолчанию вы можете предварительно просмотреть участок размером 256 на 256 пикселей в центре изображения. Чтобы изменить это, нажмите Изменить вид…

Рис. 8. Изменение подмножества изображений для предварительного просмотра классификации

Появится окно выбора пространственного подмножества , в котором вы можете выбрать другую область изображения. Сделать это можно двумя способами. Вы можете ввести точные экранные координаты левого верхнего угла фрагмента изображения.Для этого используйте поля Samples и Lines . Но, скорее всего, вам нравится визуальный образ. Чтобы использовать эту опцию, нажмите кнопку Image в окне Select Spatial Subset (Рис. 8, слева). Появится окно подмножества по изображению , оно показывает все изображение в уменьшенном масштабе, а красный прямоугольник выделяет область предварительного просмотра (Рис. 8, справа). Щелкните левой кнопкой мыши по красному окну. Удерживая левую кнопку мыши, перетащите поле в новое место и нажмите кнопку «ОК».Нажмите OK в окне Select Spatial Subset , и изображение предварительного просмотра обновится автоматически.

11) Если результаты предварительного просмотра не выглядят удовлетворительными, измените значения стандартного отклонения. После этого снова запустите предварительный просмотр. Итак, методом проб и ошибок вы найдете оптимальное значение максимального отклонения и получите результат классификации качества.

VK

Facebook

Twitter

Google+

LinkedIn

Младший научный сотрудник Регионального федерального центра аэрокосмического и наземного мониторинга объектов и природных ресурсов Национального исследовательского университета БелГУ.

,3 $, то объем параллелепипеда, образованного между этими тремя векторами, можно вычислить по следующей формуле: $ \ mathrm {Volume} = \ mathrm {abs} (\ vec {u} \ cdot (\ vec {v} \ times \ vec {w})) = \ mathrm {abs} \ begin {vmatrix} u_1 & u_2 & u_3 \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \ end {vmatrix} $.

• Доказательство: Напомним, что формула параллелепипеда определяется формулой $ V = (\ mathrm {Area \: of \: base}) (\ mathrm {height}) $. Площадь основания параллелепипеда будет площадью параллелограмма, определяемой векторами $ \ vec {u} $ и $ \ vec {v} $, которые мы уже вычислили как $ A = \ | \ vec {u} \ times \ vec {v} \ | $.Теперь нам нужно рассчитать высоту параллелепипеда.

• Сначала давайте посмотрим на следующее изображение:

• Заметим, что высота параллелепипеда — это просто норма проекции векторного произведения $ \ vec {u} \ times \ vec {v} $ на $ \ vec {w} $, то есть $ h = \ | \ mathrm {proj} _ {\ vec {u} \ times \ vec {v}} \ vec {w} \ | $. S

(1)

\ begin {align} h = \ | \ mathrm {proj} _ {\ vec {u} \ times \ vec {v}} \ vec {w} \ | = \ frac {\ mid \ vec {w} \ cdot (\ vec {u} \ times \ vec {v}) \ mid} {\ | \ vec {u} \ times \ vec {v} \ |} \ end {align}

• Подставляя это обратно в нашу формулу для объема параллелепипеда, получаем:

(2)

\ begin {align} V = \ | \ vec {u} \ times \ vec {v} \ | \ frac {\ mid \ vec {w} \ cdot (\ vec {u} \ times \ vec {v}) \ mid} {\ | \ vec {u} \ times \ vec {v} \ |} \\ V = \ mid \ vec {w} \ cdot (\ vec {u} \ times \ vec {v}) \ mid \ end {align}

• Отметим, что эта формула дает абсолютное значение тройного скалярного произведения между векторами $ \ vec {u}, \ vec {v}, \ vec {w} $, то есть:

(3)

\ begin {align} V = \ mathrm {abs} \ begin {vmatrix} w_1 & w_2 & w_3 \\ v_1 & v_2 & v_3 \\ u_1 & u_2 & u_3 \ end {vmatrix} \ end {align}

• Конечно, перестановка строк в этом определителе не влияет на определитель, когда мы вычисляем абсолютное значение результата, и поэтому наше доказательство завершено.3 $ — это ноль. Поскольку каждый вектор в $ \ {\ vec {u}, \ vec {v}, \ vec {w} \} $ уже должен лежать в той же плоскости, что и другой вектор из набора, то, поскольку объем равен нулю, должны существовать вектор в этом наборе, лежащий в той же плоскости, что и два других. Без ограничения общности предположим, что $ \ vec {u} $ лежит на одной плоскости с $ \ vec {v} $ и $ \ vec {w} $. Тогда $ \ vec {v} $ также должен лежать на той же плоскости, что и $ \ vec {u} $ и $ \ vec {w} $, и то же самое касается $ \ vec {w} $. Следовательно, все три вектора лежат в одной плоскости.3 $ и $ \ vec {u} = (1, 0, 1) $, $ \ vec {v} = (1, 1, 0) $ и $ \ vec {w} = (w_1, 0, 1) $, найдите значение $ w_1 $, при котором все три вектора лежат в одной плоскости.

  Как мы только что узнали, три вектора лежат на одной плоскости, если их тройное скалярное произведение равно нулю, и поэтому мы должны оценить следующий определитель как равный нулю:

  (4)

  \ begin {align} \ begin {vmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \\ w_1 & 0 & 1 \ end {vmatrix} = 0 \ end {align}

  Давайте оценим этот определитель по третьей строке, чтобы получить $ w_1 \ begin {vmatrix} 0 & 1 \\ 1 & 0 \ end {vmatrix} + \ begin {vmatrix} 1 & 0 \\ 1 & 1 \ end {vmatrix} = 0 $, что при упрощении равно $ -w_1 + 1 = 0 $.Следовательно, если $ w_1 = 1 $, то все три вектора лежат в одной плоскости.

  ,