Объемные фигуры все: Объёмные геометрические фигуры и их названия. Геометрические фигуры. Играем в геометрическое лото
Объёмные геометрические фигуры и их названия. Геометрические фигуры. Играем в геометрическое лото
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Чукур Людмила Васильевна
Геометрические фигуры. Особенности восприятия детьми формы предметов и геометрических фигур
«ГЕОМЕТРИЧЕСКАЯ ФИГУРА
.
ОСОБЕННОСТИ ВОСПРИЯТИЯ ДЕТЬМИ
Подготовила
: ст. воспитатель Чукур Л
. В.
1. Понятие «геометрическая фигура
»
. Особенности развития представлений о форме предметов
у детей дошкольного возраста
Одним из свойств окружающих предметов является их форма
. Форма предметов
Форма предметов
получила обобщенное отражение в геометрических фигурах
.
Фигура — латинское слово
, означает «образ»
, «вид»
, «начертание»
; это часть плоскости, ограниченная замкнутой линией, или часть пространства, ограниченная замкнутой поверхностью. Этот термин вошел в общее употребление в XII в. До этого чаще употреблялось другое латинское слово — «форма
»
, также означающее «наружный вид»
, «внешнее очертание предмета
»
.
Наблюдая за предметами окружающего мира
, люди заметили, что есть некоторое общее свойство, позволяющее объединить предметы в одну группу
. Это свойство было названо геометрической фигурой
. Геометрическая фигура – это эталон для определения формы предмета
, всякое непустое множество точек; обобщенное абстрактное понятие.
Само определение понятия геометрической фигуры дали древние греки
. Они определили
, что геометрической фигурой
является внутренняя область, ограниченная замкнутой линией на плоскости. Активно это понятие применял в своей работе Евклид. Древние греки классифицировали все геометрические фигуры и дали им названия
.
Упоминание о первых геометрических фигурах
встречается и у древних египтян и древних шумеров. Учеными-археологами был найден папирусный свиток с геометрическими задачами
, в которых упоминались геометрические фигуры
. И каждая из них называлась каким-то определенным словом
.
Таким образом, представление о геометрии
и изучаемых этой наукой фигурах
имели люди с давних времен, но название, «геометрическая фигура
»
и названия всем геометрическим фигурам
дали древнегреческие ученые.
В наше время знакомство с геометрическими фигурами
начинается с раннего детства и продолжается на всём пути обучения. Дошкольники, познавая окружающий мир, сталкиваются с разнообразием форм предметов
, учатся называть и различать их, а затем знакомятся и со свойствами геометрических фигур
.
Форма
– это внешнее очертание предмета
. Множество форм бесконечно
.
Представления о форме предметов
возникают у детей достаточно рано. В исследованиях Л. А. Венгера выясняется, возможно ли различение формы предметов детьми
, у которых еще не сформировался акт хватания
. В качестве индикатора он использовал ориентировочную реакцию ребенка в возрасте 3-4 месяцев.
Детям предъявлялись
два объемных тела одинакового стального цвета и размера (призма и шар, одно из них подвешивалась над манежем, чтобы угасить ориентировочную реакцию; затем снова подвешивалась пара фигур
. На одну из них (призма)
реакция угашена, другая (шар)
— новая. Малыши обращали взор на новую фигуру
и фиксировали ее взглядом в течение более длительного времени, чем старую.
Л. А. Венгер заметил также, что что на геометрической фигуре
с изменением пространственной ориентации возникает такое же зрительное сосредоточение, как и на новой геометрической фигуре
.
Исследования М. Денисовой и Н. Фигурина показали
, что грудной ребенок по форме на ощупь определяет бутылочку
, соску, материнскую грудь. Зрительно дети начинают различать форму предметов с 5 месяцев
. При этом индикатором различения являются движения рук, корпуса по направлению к экспериментальному объекту и схватывание его (при пищевом подкреплении)
.
В других исследованиях выявлено, что, если предметы отличаются цветом
, то ребенок 3-х лет выделяет их форму только в том случае
, если предмет
знаком ребенку из практического опыта (опыт манипуляций, действий)
.
Это доказывает и тот факт, что ребенок одинаково узнает прямые и перевернутые изображения (может рассматривать и понимать знакомые картинки, держа книжку «вверх ногами»
, предметы
, окрашенные в несвойственные цвета (черное яблоко, но квадрат, повернутый на угол, т. е. в виде ромба, не узнает, так как исчезает непосредственное сходство формы предмета
, которого нет в опыте.
2. Особенности восприятия детьми
дошкольного возраста формы предметов и геометрических фигур
Одним из ведущих познавательных процессов детей дошкольного возраста является восприятие
. Восприятие
помогает отличить один предмет от другого
, выделить какие-то предметы
или явления из других похожих на него.
Первичное овладение формой предмета
Форма предмета
, как таковая, не предмета
предшествовать
практическим действиям. Действия детей с предметами
на разных этапах различны.
Исследования психолога С. Н. Шабалина показывают, что геометрическая фигура воспринимается
дошкольниками своеобразно. Если взрослый воспринимает
ведро или стакан как предметы
, имеющие цилиндрическую форму
, то в его восприятие включается знание геометрических форм
. У дошкольника происходит обратное явление.
В 3-4 года дети опредмечивают геометрические фигуры
, так как они в их опыте представлена нераздельно с предметами
, не абстрагированы. Геометрическая фигура воспринимается детьми как картинка
, как некоторый предмет
: квадрат — это платочек, кармашек; треугольник — крыша, круг — колесо, мячик, два круга рядом — очки, несколько кругов рядом — бусы и т. п.
В 4 года опредмечивание геометрической фигуры
возникает только при столкновении ребенка с незнакомой фигурой
: цилиндр — это ведро, стаканчик.
В 4-5 лет ребенок начинает сравнивать геометрическую фигуру с предметом
: про квадрат говорит «это как платочек»
.
В результате организованного обучения дети начинают выделять в окружающих предметах знакомую геометрическую фигуру
, сравнивать предмет с фигурой
(стаканчик как цилиндр, крыша как треугольник, учится давать правильное название геометрической фигуры и формы предмета
, в их речи появляются слова «квадрат»
, «круг»
, «квадратный»
, «круглый»
и т. п.
п.
Проблему знакомства детей с геометрическими фигурами
и их свойствами следует рассматривать в двух аспектах
:
В плане сенсорного восприятия форм геометрических фигур
и использования их как эталонов в познании форм окружающих предметов
;
В смысле познания особенностей их структуры
, свойств, основных свя-зей и закономерностей в их построении, т. е. собственно геометри-ческого материала
.
Контур предмета это общее начало
, которое является исходным как для зрительного, так и для осязательного восприятия
. Однако вопрос о роли контура в восприятии формы и формировании
целостного образа требует еще дальнейшей разработки.
Первичное овладение формой предмета
осуществляется в действиях с ним. Форма предмета
, как таковая, не воспринимается отдельно от предмета
, она является его неотъемлемым признаком. Специфические зрительные реакции прослеживания контура предмета
появляются в конце второго года жизни и начинают предшествовать
практическим действиям.
Действия детей с предметами
на разных этапах различны. Малыши стремятся, прежде всего, захватить предмет
руками и начать манипулировать им. Дети 2,5 лет, прежде чем действовать, довольно подробно зрительно и осязательно — двигательно знакомятся с предметами
. Значение практических действий остается главным. Отсюда следует вывод о необходимости руководить развитием перцептивных действий двухлетних детей. В зависимости от педагогического руководства характер перцептивных действий детей постепенно достигает познавательного уровня. Ребенка начинают интересовать различные признаки предмета
, в том числе и форма
. Однако он еще долго не может выделить и обобщить тот или иной признак, в том числе и форму разных предметов
.
Сенсорное восприятие формы предмета
должно быть направлено не только на то, чтобы видеть
, узнавать формы
, наряду с другими его признаками, но уметь, абстрагируя форму от вещи
, видеть ее и в других вещах
. Такому восприятию формы предметов и ее обобщению и способствует знание детьми эталонов — геометрических фигур
Такому восприятию формы предметов и ее обобщению и способствует знание детьми эталонов — геометрических фигур
. Поэтому задачей сенсорного развития является формирование
у ребенка умений узнавать в соответствии с эталоном (той или иной геометрической фигурой
)
форму разных предметов
.
Экспериментальные данные Л. А. Венгера показали, что возможностью различать геометрические фигуры
обладают дети 3-4 месяцев. Сосредоточение взгляда на новой фигуре
— свидетельство этому.
Уже на втором году жизни дети свободно выбирают фигуру
по образцу из таких пар
: квадрат и полукруг, прямоугольник и треугольник. Но различать прямоугольник и квадрат, квадрат и треугольник дети могут лишь после 2,5 лет. Отбор же по образцу фигур более сложной формы
доступен примерно на рубеже 4-5 лет, а воспроизведение сложной фигуры
осуществляют дети пятого и шестого года жизни.
Под обучающим воздействием взрослых восприятие геометрических фигур
постепенно перестраивается. Геометрические фигуры начинают восприниматься детьми как эталоны
, с помощью которых познание структуры предмета
, его формы
и размера осуществляется не только в процессе восприятия той или иной формы зрением
, но и путем активного осязания, ощупывания ее под контролем зрения и обозначения словом.
Совместная работа всех анализаторов способствует более точному восприятию формы предметов
. Чтобы лучше познать предмет
, дети стремятся коснуться его рукой, взять в руки, повернуть; причем рассматривание и ощупывание различны в зависимости от формы
и конструкции познаваемого объекта. Поэтому основную роль в восприятии предмета и определении его формы имеет обследование
, осуществляемое одновременно зрительным и двигательно-осязательным анализаторами с последующим обозначением словом. Однако у дошкольников наблюдается весьма низкий уровень обследования формы предметов
; чаще всего они ограничиваются беглым зрительным восприятием
и поэтому не различают близкие по сходству фигуры
(овал и круг, прямоугольник и квадрат, разные треугольники)
.
В перцептивной деятельности детей осязательно-двигательные и зрительные приемы постепенно становятся основным способом рас-познавания формы
. Обследование фигур
не только обеспечивает целостное их восприятие
, но и позволяет ощутить их особенности
(характер, направления линий и их сочетания, образующиеся углы и вершины, ребенок учится чувственно выделять в любой фигуре
образ в целом и его части. Это дает возможность в дальнейшем сосредоточить внимание ребенка на осмысленном анализе фигуры
, сознательно выделяя в ней структурные элементы (стороны, углы, вершины)
. Дети уже осознанно начинают понимать и такие свойства, как устойчивость, неустойчивость и др., понимать, как образуются вершины, углы и т. д. Сопоставляя объемные и плоские фигуры
, дети находят уже общность между ними («У куба есть квадраты»
, «У бруса — прямоугольники, у цилиндра — круги»
и т. д.).
Сравнение фигуры с формой того или иного предмета
помогает детям понять, что с геометрическими фигурами
можно сравнивать разные предметы или их части
. Так, постепенно геометрическая фигура
становится эталоном определения формы предметов
.
3. Особенности
обследования и этапы обучения обследованию детьми
дошкольного возраста формы предметов и геометрических фигур
Известно, что в основе познания всегда лежит сенсорное обследование, опосредованное мышлением и речью. В исследованиях Л. Венгера с детьми
2-3 лет индикатором зрительного различения формы предметов служили предметные действия ребенка
.
По исследованиям С. Якобсон, В. Зинченко, А. Рузской дети 2-4 лет лучше узнавали предметы по форме
, когда предлагалось сначала ощупать предмет
, а потом найти такой же. Более низкие результаты наблюдались тогда, когда предмет воспринимался зрительно
.
Исследования Т. Гиневской раскрывают особенности
движений рук при обследовании предметов по форме
. Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания
Детям завязывали глаза и предлагали ознакомиться с предметом путем осязания
.
В 3-4 года – движения исполнительные (катают, стучат, возят)
. Движения немногочисленны, внутри фигуры
, иногда (однократно)
по осевой линии, много ошибочных ответов, смешение разных фигур
. В 4-5 лет – движения установочные (зажимают в руке)
. Количество движений увеличивается в два раза; судя по траектории, ориентированы на размер и площадь; крупные, размашистые, обнаруживаются группы близко расположенных фиксаций, относящихся к наиболее характерным признакам фигуры
; дают более высокие результаты. В 5-6лет – движения обследовательские (прослеживание контура, проверка на упругость)
. Появляются движения, прослеживающие контур, однако они охватывают наиболее характерную часть контура, другие части оказываются необследованными; движения внутри контура, количество то же, высокие результаты; как и в предыдущий период
, наблюдается смешение близких фигур
. В 6-7 лет – движения по контуру, пересечение поля фигуры
, причем движения сосредотачиваются на наиболее информативных признаках
, наблюдаются отличные результаты не только при узнавании, но и при воспроизведении
.
Таким образом, для того, чтобы ребенок выделил существенные признаки геометрических фигур
, необходимо их зрительное и двигательное обследование. Движения рук организовывают движения глаз и этому детей необходимо научить.
Этапы обучения обследованию
Задача первого этапа обучения детей 3-4 лет — это сенсорное восприятие формы предметов и геометрических фигур
.
Второй этап обучения детей 5-6 лет должен быть посвящен формированию системных знаний о геометрических фигурах
и развитию у них начальных приемов и способов
«геометрического мышления
»
.
«Геометрическое мышление
»
вполне возможно развить еще в дошкольном возрасте. В развитии «геометрических знаний
»
у детей прослеживается несколько различных уровней.
Первый уровень характеризуется тем, что фигура воспринимается детьми как целое
, ребенок еще не умеет выделять в ней отдельные элементы, не замечает сходства и различия между фигурами
, каждую из них воспринимает обособленно
.
На втором уровне ребенок уже выделяет элементы в фигуре
и устанавливает отношения как между ними, так и между отдельными фигурами
, однако еще не осознает общности между фигурами
.
На третьем уровне ребенок в состоянии устанавливать связи между свойствами и структурой фигур
, связи между самими свойствами. Переход от одного уровня к другому не является самопроизвольным, идущим параллельно биологическому развитию человека и зависящим от возраста. Он протекает под влиянием целенаправленного обучения, которое содействует ускорению перехода к более высокому уровню. Отсутствие же обучения тормозит развитие. Обучение поэтому следует организовывать так, чтобы в связи с усвоением знаний о геометрических фигурах
у детей развивалось и элементарное геометрическое мышление
.
Познание геометрических фигур
, их свойств и отношений расширяет кругозор детей, позволяет им более точно и разносторонне воспринимать форму окружающих предметов
, что положительно отражается на их продуктивной деятельности (например, рисовании, лепке)
.
Большое значение в развитии геометрического
мышления и про-странственных представлений
имеют действия по преобразованию фигур
(из двух треугольников составить квадрат или из пяти палочек сложить два треугольника).
Все эти разновидности упражнений развивают пространственные представления и начала геометрического мышления детей
, формируют
у них умения наблюдать, анализировать, обобщать, выделять главное, существенное и одновременно с этим воспитывают
такие качества личности, как целенаправленность, настойчивость.
Итак, в дошкольном возрасте происходит овладение перцептивной и интеллектуальной систематизацией форм геометрических фигур
. Перцептивная деятельность в познании фигур
Перцептивная деятельность в познании фигур
опережает развитие интеллектуальной систематизации.
Библиографический список
1. Белошистая А. В. Знакомство с геометрическими понятиями / А
. Белошистая // Дошкольное воспитание
. — 2008. — № 9. — с. 41- 51
2. Венгер Л. А. Воспитание
сенсорной культуры ребенка / Л. А. Венгер Э. Г. Пилюгина, Н. Б. Венгер. — М.
: Просвещение, 1988.- 144с.
3. Воспитание
и обучение детей пятого года жизни
: книга для воспитателя детского сада /
(А. Н. Давидчук, Т. И. Осокина, Л. А. Парамонова и др.)
; под ред. В. В. Холмовской. — М.
: Просвещение, 1986. — 144 с.
4. Габова М. А. Знакомство детей с геометрическими фигурами / М
. А. Габова // Дошкольное воспитание
. — 2002. — № 9. — с. 2- 17.
5. Дидактические игры и упражнения по сенсорному воспитанию дошкольников
: (пособие для воспитателя
детского сада / под ред. Л. А. Венгера). — М.
: Просвещение, 1978. — 203 с.
6. Кербс Е. В. Математические досуги / Е. В. Кербс // Ребёнок в детском саду. — 2008. — № 3. — с. 21- 23.
7.Математика в детском саду
: (пособие для воспитателя дет
. сада / составитель Г. М. Лямина). — М.
: Просвещение, 1977. — С. 224 — 228.
8. Метлина Л. С.Математика в детском саду
: (пособие для воспитателя дет
. сада)
/ Л. С. Метлина. — М.
: Просвещение, 1994. — 256 с.
Геометрические фигуры представляют собой комплекс точек, линий, тел или поверхностей. Эти элементы могут располагаться как на плоскости, так и в пространстве, формируя конечное количество прямых.
Термин «фигура» подразумевает под собой несколько множеств точек. Они должны располагаться на одной или нескольких плоскостях и одновременно ограничиваться конкретным числом оконченных линий.
Основными геометрическими фигурами считаются точка и прямая. Они располагаются на плоскости. Кроме них, среди простых фигур выделяют луч, ломаную линию и отрезок.
Точка
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. В геометрии ее принято обозначать буквой латинской алфавита, к примеру, A, B, K, L.
С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии. Этот нульмерный объект просто не имеет определения.
Прямая
Это фигура полностью размещается в одной плоскости. У прямой нет конкретного математического определения, так как она состоит из огромного количества точек, располагающихся на одной бесконечной линии, у которой нет предела и границ.
Существует еще и отрезок. Это тоже прямая, но она начинается и заканчивается с точки, а значит, имеет геометрические ограничения.
Также линия может превратиться в направленный луч. Такое происходит, когда прямая начинается с точки, но четкого окончания не имеет. Если же поставить точку посредине линии, то она разобьется на два луча (дополнительных), причем противоположно направленных друг к другу.
Несколько отрезков, которые последовательно соединяются друг с другом концами в общей точке и располагаются не на одной прямой, принято называть ломаной линией.
Угол
Геометрические фигуры, названия которых мы рассмотрели выше, считают ключевыми элементами, использующимися при построении более сложных моделей.
Угол — это конструкция, состоящая из вершины и двух лучей, которые выходят из нее. То есть стороны этой фигуры соединяются в одной точке.
Плоскость
Рассмотрим еще одно первичное понятие. Плоскость — это фигура, у которой нет ни конца, ни начала, равно как и прямой, и точки. Во время рассмотрения этого геометрического элемента во внимание берется лишь его часть, ограниченная контурами ломаной замкнутой линии.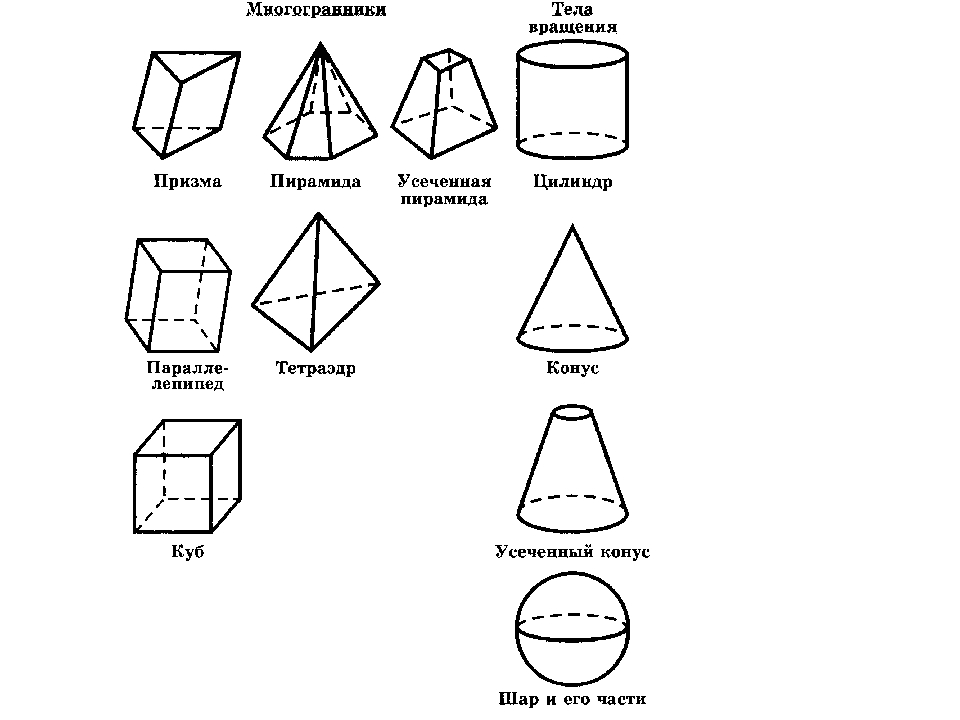
Любую гладкую ограниченную поверхность можно считать плоскостью. Это может быть гладильная доска, лист бумаги или даже дверь.
Четырехугольники
Параллелограмм — это геометрическая фигура, противоположные стороны которой параллельны друг другу попарно. Среди частных видов этой конструкции выделяют ромб, прямоугольник и квадрат.
Прямоугольник — это параллелограмм, у которого все стороны соприкасаются под прямым углом.
Квадрат — это четырехугольник с равными сторонами и углами.
Ромб — это фигура, у которой все грани равны. При этом углы могут быть совершенно разными, но попарно. Каждый квадрат считается ромбом. Но в противоположном направлении это правило действует не всегда. Далеко не каждый ромб является квадратом.
Трапеция
Геометрические фигуры бывают совершенно разными и причудливыми. Каждая из них имеет своеобразную форму и свойства.
Трапеция — это фигура, которая чем-то схожа с четырехугольником. Она имеет две параллельные противоположные стороны и при этом считается криволинейной.
Круг
Эта геометрическая фигура подразумевает расположение на одной плоскости точек, равноудаленных от ее центра. При этом заданный ненулевой отрезок принято называть радиусом.
Треугольник
Это простая геометрическая фигура, которая очень часто встречается и изучается.
Треугольник считается подвидом многоугольника, расположенным на одной плоскости и ограниченным тремя гранями и тремя точками соприкосновения. Эти элементы попарно соединены между собой.
Многоугольник
Вершинами многоугольников называют точки, соединяющие отрезки. А последние, в свою очередь, принято считать сторонами.
Объемные геометрические фигуры
- призма;
- сфера;
- конус;
- цилиндр;
- пирамида;
Эти тела имеют нечто общее. Все они ограничиваются замкнутой поверхностью, внутри которой находится множество точек.
Объемные тела изучают не только в геометрии, но и в кристаллографии.
Любопытные факты
Наверняка вам будет интересно ознакомиться с информацией, предоставленной ниже.
- Геометрия сформировалась как наука еще в давние века. Это явление принято связывать с развитием искусства и разнообразных ремесел. А названия геометрических фигур свидетельствуют об использовании принципов определения подобия и схожести.
- В переводе с древнегреческого термин «трапеция» обозначает столик для трапезы.
- Если вы возьмете различные фигуры, периметр которых будет одинаковым, то наибольшая площадь гарантированно будет у круга.
- В переводе с греческого языка термин «конус» обозначает сосновую шишку.
- Существует известная картина Каземира Малевича, которая начиная с прошлого века притягивает к себе взгляды многих живописцев. Работа «Черный квадрат» всегда была мистической и загадочной. Геометрическая фигура на белом полотне восхищает и поражает одновременно.
Существует большое количество геометрических фигур. Все они отличаются параметрами, а порой даже удивляют формами.
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.
Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами.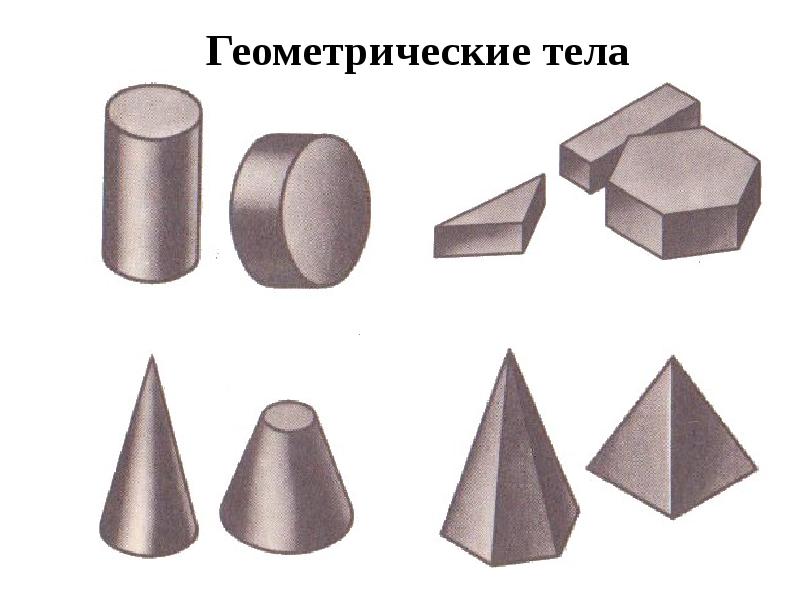 Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)
Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.
Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.
В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.
Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.
Ромб
Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.
Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.
Приемы запоминания
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
- Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.
- Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор – очень много интересных сочетаний можно выложить, комбинируя разные фигурки.
- Купите линейку с отверстиями в форме круга, квадрата, треугольника и других – для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки – интереснейшее занятие.
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Геометрические объемные фигуры — это твердые тела, которые занимают ненулевой объем в евклидовом (трехмерном) пространстве. Эти фигуры изучает раздел математики, который носит название «пространственная геометрия». Знания о свойствах объемных фигур применяются в инженерии и в науках о природе. Рассмотрим в статье вопрос, геометрические объемные фигуры и их названия.
Геометрические объемные тела
Поскольку эти тела имеют конечную размерность в трех пространственных направлениях, то для их описания в геометрии используют систему из трех координатных осей. Эти оси обладают следующими свойствами:
- Они ортогональны друг другу, то есть перпендикулярны.
- Эти оси нормализированы, то есть базисные вектора каждой оси имеют одинаковую длину.
- Любая из осей координат — это результат векторного произведения двух других.
Говоря о геометрических объемных фигурах и их названиях, следует отметить, что все они принадлежат к одному из 2-х больших классов:
- Класс полиэдров.
 Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2. - Класс круглых тел или тел вращения. Эти фигуры имеют хотя бы одну поверхность, образующую их, изогнутой формы. Например, шар, конус, цилиндр, тор.
Что касается свойств объемных фигур, то следует выделить два самых важных из них:
- Наличие определенного объема, который фигура занимает в пространстве.
- Наличие у каждой объемной фигуры площади поверхности.
Оба свойства для каждой фигуры описываются конкретными математическими формулами.
Рассмотрим ниже самые простые геометрические объемные фигуры и их названия: куб, пирамиду, призму, тетраэдр и шар.
Фигура куб: описание
Под геометрической фигурой куб понимают объемное тело, которое образовано 6-тью квадратными плоскостями или поверхностями. Также эту фигуру называют правильный гексаэдр, поскольку она имеет 6 сторон, или прямоугольный параллелепипед, так как он состоит из 3-х пар параллельных сторон, которые взаимно перпендикулярны друг другу. Называют куб и у которой основание является квадратом, а высота равна стороне основания.
Поскольку куб является многогранником или полиэдром, то для него можно применить теорему Эйлера, чтобы определить число его ребер. Зная, что число сторон равно 6, а вершин у куба 8, число ребер равно: Р = С + В — 2 = 6 + 8 — 2 = 12.
Если обозначить буквой «a» длину стороны куба, тогда формулы для его объема и площади поверхности будут иметь вид: V = a 3 и S = 6*a 2 , соответственно.
Фигура пирамида
Пирамида — это полиэдр, который состоит из простого многогранника (основание пирамиды) и треугольников, которые соединяются с основанием и имеют одну общую вершину (вершина пирамиды). Треугольники называются боковыми гранями пирамиды.
Треугольники называются боковыми гранями пирамиды.
Геометрические характеристики пирамиды зависят от того, какой многоугольник лежит в ее основании, а также от того, является ли пирамида прямой или косой. Под прямой пирамидой понимают такую пирамиду, для которой перпендикулярная основанию прямая, проведенная через вершину пирамиды, пересекает основание в ее геометрическом центре.
Одной из простых пирамид является четырехугольная прямая пирамида, в основании которой лежит квадрат со стороной «a», высота этой пирамиды «h». Для этой фигуры пирамиды объем и площадь поверхности будут равны: V = a 2 *h/3 и S = 2*a*√(h 2 +a 2 /4) + a 2 , соответственно. Применяя теорему Эйлера для нее, с учетом того, что число граней равно 5, и число вершин равно 5, получаем количество ребер: Р = 5 + 5 — 2 = 8.
Фигура тетраэдр: описание
Под геометрической фигурой тетраэдр понимают объемное тело, образованное 4-мя гранями. Исходя из свойств пространства, такие грани могут представлять только треугольники. Таким образом, тетраэдр является частным случаем пирамиды, у которой в основании лежит треугольник.
Если все 4-ре треугольника, образующие грани тетраэдра, являются равносторонними и равными между собой, то такой тетраэдр называется правильным. Этот тетраэдр имеет 4 грани и 4 вершины, число ребер составляет 4 + 4 — 2 = 6. Применяя стандартные формулы из плоской геометрии для рассматриваемой фигуры, получаем: V = a 3 * √2/12 и S = √3*a 2 , где a — длина стороны равностороннего треугольника.
Интересно отметить, что в природе некоторые молекулы имеют форму правильного тетраэдра. Например, молекула метана CH 4 , в которой атомы водорода расположены в вершинах тетраэдра, и соединены с атомом углерода ковалентными химическими связями. Атом углерода находится в геометрическом центре тетраэдра.
Простая в изготовлении форма фигуры тетраэдр используется также в инженерии. Например, тетраэдрическую форму используют при изготовлении якорей для кораблей.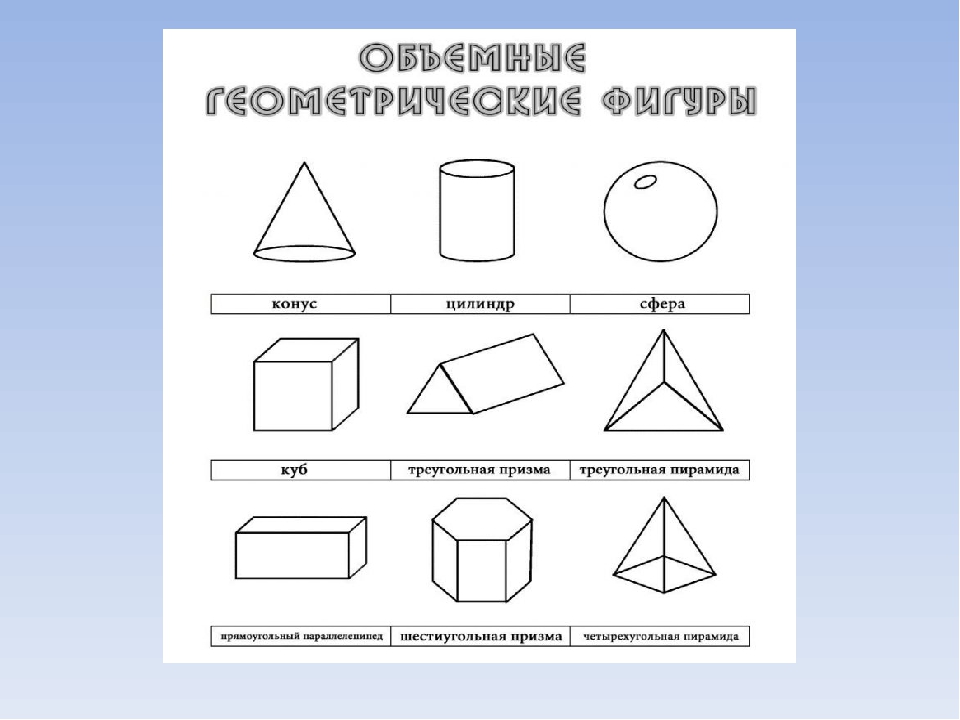 Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Отметим, что космический зонд НАСА, Mars Pathfinder, который совершил посадку на поверхность Марса 4 июля 1997 года, также имел форму тетраэдра.
Фигура призма
Эту геометрическую фигуру можно получить, если взять два многогранника, расположить их параллельно друг другу в разных плоскостях пространства, и соединить их вершины соответствующим образом между собой. В итоге получится призма, два многогранника называются ее основаниями, а поверхности, соединяющие эти многогранники, будут иметь форму параллелограммов. Призма называется прямой, если ее боковые стороны (параллелограммы) являются прямоугольниками.
Призма — это полиэдр, поэтому для нее верна Например, если в основании призмы лежит шестиугольник, тогда, количество сторон у призмы равно 8, а количество вершин — 12. Число ребер будет равно: Р = 8 + 12 — 2 = 18. Для прямой призмы высотой h, в основании которой лежит правильный шестиугольник со стороной a, объем равен: V = a 2 *h*√3/4, площадь поверхности равна: S = 3*a*(a*√3 + 2*h).
Говоря о простых геометрических объемных фигурах и их названиях, следует упомянуть шар. Под объемным телом под названием шар понимают тело, которое ограничено сферой. В свою очередь, сфера — это совокупность точек пространства, равноудаленных от одной точки, которая называется центром сферы.
Поскольку шар относится к классу круглых тел, то для него не существует понятия о сторонах, ребрах и вершинах. сферы, ограничивающей шар, находится по формуле: S = 4*pi*r 2 , а объем шара можно вычислить по формуле: V = 4*pi*r 3 /3, где pi — число пи (3,14), r — радиус сферы (шара).
Все объемные геометрические фигуры и их названия. Старт в науке
Фигура
– это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Точка
– основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.
Линия
– это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.
Прямая линия
– это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.
Луч
– это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.
Отрезок
– это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.
Кривая линия
– это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.
Ломаная линия
– это фигура, которая состоит из отрезков, последовательно соединенных своими концами.
Вершины ломаной
– это
- точка, с которой начинается ломанная,
- точки, в которых соединяются отрезки, образующие ломаную,
- точка, которой заканчивается ломанная.
Звенья ломаной
– это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.
Незамкнутая линия
– это линия, концы которой не соединены вместе.
Замкнутая линия
– это линия, концы которой соединены вместе.
Многоугольник
– это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Цели урока
:
- Познавательная
: создать условия для ознакомления с понятиями плоские
и объёмные геометрические фигуры,
расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры. - Коммуникативная
: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку. - Регулятивная
: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность.
- Личностная
: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.
Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.
предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные
:
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные
:
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование
: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока
: изучение нового материала.
Методы
: словесные, исследовательские, наглядные, практические.
Формы работы
: фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
Чем они похожи?
Можно ли сказать, что это одно и тоже?
Чем же отличается куб от квадрата?
Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
(Ученики получают индивидуальные фигуры – куб и квадрат.)
Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
!
Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
Можно ли куб полностью (весь) прижать к парте? Проверим.
Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
!
Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры:
пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
Какую форму имеют основания этих фигур?
Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
Предложите свои названия.
Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа
:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку
.)
Группа 1.
(Для изучения параллелепипеда)
Группа 2.
(Для изучения пирамиды)
Группа 3.
(Для изучения куба)
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
Что нового вы для себя сегодня открыли?
Все геометрические фигуры можно разделить на объёмные и плоские.
А я узнал названия объёмных фигур
Тема урока
Геометрические фигуры
Что такое геометрическая фигура
Геометрические фигуры – это совокупность множества точек, линий, поверхностей или тел, которые расположены на поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Точка и прямая — это основные геометрические фигуры, расположенные на плоскости.
К самым простым геометрическим фигурам на плоскости принадлежат — отрезок, луч и ломаная линия.
Что такое геометрия
Геометрия – это такая математическая наука, которая занимается изучением свойств геометрических фигур. Если дословно перевести на русский язык термин «геометрия», то он обозначает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Практическое применение геометрии бесценно во все времена и независимо от профессии. Без знаний геометрии не может обойтись ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Вам уже известно, что фигурой называют произвольное множество точек, находящиеся на плоскости.
К геометрическим фигурам принадлежат: точка, прямая, отрезок, луч, треугольник, квадрат, круг и другие фигуры, которые изучает планиметрия.
Точка
Из выше изученного материала вам уже известно, что точка относится к главным геометрическим фигурам. И хотя это самая малая геометрическая фигура, но она необходима для построения других фигур на плоскости, чертеже или изображении и является основой для всех остальных построений. Ведь построение более сложноватых геометрических фигур складывается из множества точек, характерных для данной фигуры.
В геометрии точки обозначают прописными буквами латинского алфавита, например, такими, как: А, В, С, D ….
А теперь подведем итог, и так, с математической точки зрения, точка является таким абстрактным объектом в пространстве, который не имеет объема, площади, длины и других характеристик, но остается одним из фундаментальных понятий в математике.
Точка – это такой нульмерный объект, которые не имеет определения. По определению Евклида, точкой называют то, что невозможно определить.
Прямая
Как и точка, прямая относится к фигурам на плоскости, которая не имеет определения, так как состоит из бесконечного множества точек, находящихся на одной линии, которая не имеет ни начала ни конца. Можно утверждать, что прямая линия бесконечна и не имеет предела.
Если же прямая начинается и заканчивается точкой, то она уже не является прямой и называется отрезком.
Но иногда прямая, с одной стороны имеет точку, а с другой нет. В таком случае прямая превращается в луч.
Если же взять прямую и на ее средине поставить точку, то она разобьет прямую на два противоположно направленных луча. Данные лучи являются дополнительными.
Если же перед вами несколько отрезков, соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Задание
Какая ломаная линия называется незамкнутой?
Как обозначается прямая?
Как называется ломаная линия, у которой четыре замкнутых звена?
Какое название имеет ломаная линия с тремя замкнутыми звеньями?
Когда конец последнего отрезка ломаной совпадает с началом 1-го отрезка, то такую ломаную линию называют замкнутой. Примером замкнутой ломаной является любой многоугольник.
Плоскость
Как точка и прямая, так и плоскость является первичным понятием, не имеет определения и у нее нельзя увидеть ни начала, ни конца. Поэтому, при рассмотрении плоскости, мы рассматриваем только ту ее часть, которая ограничивается замкнутой ломаной линией. Таким образом, плоскостью можно считать любую гладкую поверхность. Этой поверхностью может быть лист бумаги или стола.
Угол
Фигура, которая имеет два луча и вершину, называется углом. Место соединения лучей, является вершиной этого угла, а его сторонами считаются лучи, которые этот угол образуют.
Задание:
1. Как в тексте обозначают угол?
2. Какими единицами можно измерить угол?
3. Какие бывают углы?
Параллелограмм
Параллелограмм — это четырехугольник, противолежащие стороны которого попарно параллельны.
Прямоугольник, квадрат и ромб являются частными случаями параллелограмма.
Параллелограмм, имеющий прямые углы равные 90 градусам, является прямоугольником.
Квадрат — это тот же параллелограмм, у него и углы и стороны равны.
Что до определения ромба, то это такая геометрическая фигура, все стороны которого равны.
Кроме того, следует знать, что любой квадрат является ромбом, но не каждый ромб может быть квадратом.
Трапеция
При рассмотрении такой геометрической фигуры, как трапеция, можно сказать, что в частности она, как и четырехугольник имеет одну пару параллельных противолежащих сторон и является криволинейной.
Окружность и круг
Окружность — геометрическое место точек плоскости, равноудалённых от заданной точки, называемой центром, на заданное ненулевое расстояние, называемое её радиусом.
Треугольник
Также к простым геометрическим фигурам принадлежит и уже изучаемый вами треугольник. Это один из видов многоугольников, у которого часть плоскости ограничена тремя точками и тремя отрезками, которые соединяют эти точки попарно. Любой треугольник имеет три вершины и три стороны.
Задание:
Какой треугольник называют вырожденным?
Многоугольник
К многоугольникам относятся геометрические фигуры разных форм, у которых замкнутая ломаная линия.
В многоугольнике все точки, которые соединяют отрезки, являются его вершинами. А отрезки, из которых состоит многоугольник, являются его сторонами.
А известно ли вам, что возникновение геометрии уходит в глубину веков и связано с развитием различных ремесел, культуры, искусства и наблюдением за окружающим миром. Да и название геометрических фигур является тому подтверждением, так как их термины, возникли не просто так, а благодаря своей схожести и подобию.
Ведь термин «трапеция» в переводе с древнегреческого языка от слова «трапезион» обозначает столик, трапеза и другие производные слова.
«Конус» произошел от греческого слова «конос», что в переводе звучит, как сосновая шишка.
«Линия» имеет латинские корни и происходит от слова «линум», в переводе это звучит, как льняная нить.
А знаете ли вы, что если взять геометрические фигуры с одинаковым периметром, то среди них обладателем самой большой площади оказался круг.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия — одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.
В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий — понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии — теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).
На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным
становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества . Таким образом, целью
данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Объект исследования
: Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.
Задачи исследования:
Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.
Теоретическая и практическая значимость исследования
состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.
Объем и структура исследования:
Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.
Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные геометрические фигуры в архитектуре зданий и сооружений
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии — планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия
(от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.
Самой простой геометрической фигурой является точка.
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.
Прямая
— одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):
Таблица 1
Параллельные прямые | Свойства параллельных прямых | |
Если прямые параллельны, то их одноименные проекции параллельны: | Ессентуки, здание грязелечебницы (фото автора) | |
Пересекающиеся прямые | Свойства пересекающихся прямых | Примеры в архитектуре зданий и сооружений |
Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи: | Здания «горы» на Тайване https://www.sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane | |
Скрещивающиеся прямые | Свойства скрещивающихся прямых | Примеры в архитектуре зданий и сооружений |
Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. Ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях. | Робер, Гюбер — Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287 |
1.2. Плоские геометрические фигуры. Свойства и определения
Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.
Четырехугольники:
Параллелограмм
(др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник — параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Трапеция—
это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Треугольник
— это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника
, а отрезки — сторонами треугольника.
Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.
Многоуго́льник —
это геометрическая фигура, обычно определяемая как замкнутая ломаная.
Круг
— геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.
Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.
Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.
Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».
Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» (греч. — «буква»).
Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5
, квадрат 6
и параллелограмм 7
. Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.
Рис.3. Элементы игры «Танграм» и геометрические фигуры
Рис.4. Задания «Танграм»
Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.
Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.
Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).
Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.
Рис. 5. Приёмы разрезаний
На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.
Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части.
Рис.6.Примеры задач на разрезание:
—— —
воссозданный квадрат; — разрез ножницами;
Основная фигура
2.2.Равновеликие и равносоставленные фигуры
Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.
Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F
на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.
Отсюда вытекает следующая теорема:
равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.
На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).
Рис.7. Преобразование «греческого креста»
В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет.
Рис.8. Паркет, собранный из греческого креста
Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.
Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.
Отметим, что для приведенной выше теоремы справедлива и обратная теорема:
если два многоугольника равновелики, то они равносоставлены.
Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.
Заключение
В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.
Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.
В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».
Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.
Библиографический список
1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. — Нижний Новгород: Изд-во НГТУ, 2002. — 73 с.
2. Энциклопедический словарь юного математика /Сост. А.П. Савин. — М.: Педагогика, 1985. — 352 с.
3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053
Приложение 1
Анкета-опросник для одноклассников
1. Знаете ли вы, что такое головоломка «Танграм»?
2. Что такое «греческий крест»?
3. Было бы вам интересно узнать, что такое «Танграм»?
4. Было бы вам интересно узнать, что такое «греческий крест»?
Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.
Приложение 2
Элементы игры «Танграм» и геометрические фигуры
Преобразование «греческого креста»
Существует бесконечное множество форм. Формой называют внешнее очертание предмета.
Изучение форм можно начинать с самого раннего детства, обращая внимание своего ребенка на окружающий нас мир, который состоит из фигур (тарелка – круглая, телевизор – прямоугольный).
Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник.
Сначала он их должен просто показывать, когда вы это просите. А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника.
Чем больше упражнений на закрепление форм будет выполнено ребенком, тем больше новых фигур он запомнит.
Будущий первоклашка должен знать все простые геометрические фигуры и уметь составлять из них аппликации.
Что мы называем геометрической фигурой?
Геометрическая фигура — это эталон, с помощью которого можно определить форму предмета или его частей.
Фигуры разделяют на две группы: плоские фигуры, объемные фигуры.
Плоскими фигурами мы назовем те фигуры, которые расположены в одной плоскости. К ним относятся круг, овал, треугольник, четырёхугольник (прямоугольник, квадрат, трапеция, ромб, параллелограмм) и всевозможные многоугольники.
К объемным фигурам относят: сфера, куб, цилиндр, конус, пирамида. Это те фигуры, которые имеют высоту, ширину и глубину.
Следуйте двум простым советам при объяснении геометрических фигур:
- Терпение. То, что нам, взрослым, кажется простым и логичным ребенку покажется просто непонятным.
- Попробуйте рисовать фигуры вместе с ребенком.
- Игра. Начинайте изучать фигуры в игровой форме. Хорошие упражнения для закрепления и изучения плоских форм – аппликации из геометрических фигур. Для объемных – можно использовать готовые покупные игры, а также выбирать аппликации, где можно вырезать и склеивать объемную форму.
|
Виды объемных геометрических фигур и их названия. Геометрические фигуры плоские и объёмные
Геометрические фигуры — это замкнутые множества точек на плоскости или в пространстве, которые ограничены конечным числом линий. Они могут быть линейными (1D), плоскими (2D) или пространственными (3D).
Любое тело, имеющее форму, представляет собой совокупность геометрических фигур.
Любую фигуру можно описать математической формулой различной степени сложности. Начиная от простого математического выражения до суммы рядов математических выражений.
Основными математическими параметрами геометрических фигур являются радиусы, длины сторон или граней и углы между ними.
Ниже представлены основные геометрические фигуры, наиболее часто используемые в прикладных расчетах, формулы и ссылки на расчетные программы.
Линейные геометрические фигуры
1. Точка
Точка — это базовый объект измерения. Основной и единственной математической характеристикой точки является её координата.
2. Линия
Линия — это тонкий пространственный объект имеющий конечную длину и представляющий собой цепь связанных друг с другом точек. Основной математической характеристикой линии является длина.
Луч — это тонкий пространственный объект имеющий бесконечную длину и представляющий собой цепь связанных друг с другом точек. Основными математическими характеристиками луча являются координата его начала и направление.
Плоские геометрические фигуры
1. Круг
Круг — это геометрическое место точек на плоскости, расстояние от которых до его центра, не превышает заданного числа, называемого радиусом этого круга. Основной математической характеристикой круга является радиус.
2. Квадрат
Квадрат — это четырёхугольник, у которого все углы и все стороны равны. Основной математической характеристикой квадрата является длина его стороны.
3. Прямоугольник
Прямоугольник — это четырехугольник, у которого все углы равны 90 градусам (прямые). Основными математичскими характеристиками прямоугольника являются длины его сторон.
4. Треугольник
Треугольник — это геометрическая фигура, образованная тремя отрезками, которые соединяют три точки (вершины треугольника), не лежащие на одной прямой. Основными математическими характеристиками треугольника являются длины сторон и высота.
5. Трапеция
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Основными математическими характеристиками трапеции являются длины сторон и высота.
6. Параллелограмм
Параллелограмм — это четырёхугольник, у которого противоположные стороны параллельны. Основными математическими характеристиками параллелограмма являются длины его сторон и высота.
Ромб — это четырехугольник, у которого все стороны, а углы его вершин не равны 90 градусам. Основными математическими характеристиками ромба являются длина его стороны и высота.
8. Эллипс
Эллипс — это замкнутая кривая на плоскости, которая может быть представлена как ортогональная проекция сечения окружности цилиндра на плоскость. Основными математическими характеристиками окружности являются длина его полуосей.
Объемные геометрические фигуры
1. Шар
Шар — это геометрическое тело, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой шара является его радиус.
Сфера — это оболочка геометрического тела, представляющее собой совокупность всех точек пространства, находящихся от его центра на заданном расстоянии. Основной математической характеристикой сферы является её радиус.
Куб — это геометрическое тело, представляющее собой правильный многогранник, каждая грань которого представляет собой квадрат. Основной математической характеристикой куба является длина его ребра.
4. Параллелепипед
Параллелепипед — это геометрическое тело, представляющее собой многогранник, у которого шесть граней и каждая из них прямоугольник. Основными математическими характеристиками параллелепипеда являются длины его ребер.
5. Призма
Призма — это многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани параллелограммами, имеющими общие стороны с этими многоугольниками. Основными математическими характеристиками призмы являются площадь основания и высота.
Конус — это геометрическая фигура, полученная объединением всех лучей, исходящих из одной вершины конуса и проходящих через плоскую поверхность. Основными математическими характеристиками конуса являются радиус основания и высота.
7. Пирамида
Пирамида — это многогранник, основанием которого является произвольный многоугольник, а боковые грани являются треугольниками, имеющие общую вершину. Основными математическими характеристиками пирамиды являются площадь основания и высота.
8. Цилиндр
Цилиндр — это геометрическая фигура, ограниченная цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Основными математическими характеристиками цилиндра являются радиус основания и высота.
Быстро выполнить эти простейшие математические операции можно с помощью наших онлайн программ. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.
На этой странице представлены все геометрические фигуры, которые наиболее часто встречаются в геометрии для представления объекта или его части на плоскости или в пространстве.
Маленькие детки готовы учиться везде и всегда. Их юный мозг способен улавливать, анализировать и запоминать столько информации, сколько трудно даже взрослому человеку. То, чему родители должны научить малышей, имеет общепринятые возрастные рамки.
Основные геометрические фигуры и их названия дети должны узнать в возрасте от 3 до 5 лет.
Поскольку все дети разнообучаемы, то эти границы лишь условно приняты в нашей стране.
Геометрия – это наука о формах, размерах и расположении фигур в пространстве. Может создаться впечатление, что это сложно для малышей. Однако предметы изучения этой науки находятся повсюду вокруг нас. Вот почему иметь основные познания в этой области важно и для детей, и для старших.
Чтобы увлечь детей изучением геометрии, можно прибегнуть к веселым картинкам. Дополнительно хорошо бы иметь пособия, которые ребенок сможет потрогать, ощупать, обвести, раскрасить, узнать с закрытыми глазами. Основной принцип любых занятий с детьми – удержание их внимание и развития тяги к предмету с использованием игровых приемов и непринужденной веселой обстановки.
Сочетание нескольких средств восприятия сделает свое дело очень быстро. Воспользуйтесь нашей мини-методичкой, чтобы научить ребенка отличать геометрические фигуры, знать их названия.
Круг – самая первая из всех фигур. В природе вокруг нас многое имеет круглую форму: наша планета, солнце, луна, сердцевина цветка, многие фрукты и овощи, зрачки глаз. Объемный круг – это шар (мячик, клубок)
Начать изучение формы круга с ребенком лучше, рассматривая рисунки, а потом уже подкрепить теорию практикой, дав ребенку подержать что-нибудь круглое в руках.
Квадрат – это фигура, у которой все стороны имеют одинаковую высоту и ширину. Квадратные предметы – кубики, коробки, дом, окно, подушка, табурет и т. п.
Строить из квадратных кубиков всякие домики очень просто. Рисунок квадрата проще сделать на листочке в клетку.
Прямоугольник – родственник квадрата, который отличается тем, что имеет одинаковые противоположные стороны. Так же, как и у квадрата, у прямоугольника все равны 90 градусам.
Можно найти множество предметов, имеющих форму прямоугольника: шкафы, бытовая техника, двери, мебель.
В природе форму треугольника имеют горы и некоторые деревья. Из ближайшего окружения малышей можно привести в пример треугольную крышу дома, различные дорожные знаки.
В форме треугольника были построены некоторые древние сооружения, например храмы и пирамиды.
Овал – это круг, вытянутый с двух сторон. Формой овала обладают, например: яйцо, орехи, многие овощи и фрукты, человеческое лицо, галактики т. д.
Овал в объеме называется эллипсом. Даже Земля сплюснута с полюсов – эллипсовидная.
Ромб
Ромб – тот же квадрат, только вытянутый, т. е. имеет два тупых угла и пару острых.
Изучать ромб можно с помощью наглядных пособий – нарисованной картинки или объемного предмета.
Приемы запоминания
Геометрические фигуры по названиям запомнить несложно. В игру их изучение для детей можно превратить, применив следующие идеи:
- Купите детскую книжку с картинками, в которой будут веселые и красочные рисунки фигур и их аналогии из окружающего мира.
- Нарежьте из разноцветного картона побольше всяких фигурок, заламинируйте их скотчем и используйте как конструктор – очень много интересных сочетаний можно выложить, комбинируя разные фигурки.
- Купите линейку с отверстиями в форме круга, квадрата, треугольника и других – для детей, которые уже дружат с карандашами, рисунки с помощью такой линейки – интереснейшее занятие.
Можно придумать много возможностей научить малышей знать названия геометрических фигур. Все способы хороши: рисунки, игрушки, наблюдения за окружающими предметами. Начните с малого, постепенно усложняя информацию и задания. Вы не ощутите, как пролетит время, а малыш обязательно порадует вас успехами в скором.
Фигура
– это произвольное множество точек на плоскости. Точка, прямая, отрезок, луч, треугольник, круг, квадрат и так далее – всё это примеры геометрических фигур.
Точка
– основное понятие геометрии, это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.
Линия
– это множество точек, последовательно расположенных друг за другом. У линии измеряют только длину. Ширины и толщины она не имеет.
Прямая линия
– это линия, которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны.
Луч
– это часть прямой линии, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону.
Отрезок
– это часть прямой линии, ограниченная двумя точками. Отрезок имеет начало и конец, поэтому можно измерить его длину.
Кривая линия
– это плавно изгибающаяся линия, которая определяется расположением составляющих её точек.
Ломаная линия
– это фигура, которая состоит из отрезков, последовательно соединенных своими концами.
Вершины ломаной
– это
- точка, с которой начинается ломанная,
- точки, в которых соединяются отрезки, образующие ломаную,
- точка, которой заканчивается ломанная.
Звенья ломаной
– это отрезки, из которых состоит ломаная. Количество звеньев ломаной всегда на 1 меньше, чем количество вершин ломаной.
Незамкнутая линия
– это линия, концы которой не соединены вместе.
Замкнутая линия
– это линия, концы которой соединены вместе.
Многоугольник
– это замкнутая ломанная линия. Вершины ломаной называются вершинами многоугольника, а отрезки — сторонами многоугольника.
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Геометрия — одна из важнейших компонент математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, а также для эстетического воспитания. Изучение геометрии вносит вклад в развитие логического мышления, формирование навыков доказательства.
В курсе геометрии 7 класса систематизируются знания о простейших геометрических фигурах и их свойствах; вводится понятие равенства фигур; вырабатывается умение доказывать равенство треугольников с помощью изученных признаков; вводится класс задач на построение с помощью циркуля и линейки; вводится одно из важнейших понятий — понятие о параллельных прямых; рассматриваются новые интересные и важные свойства треугольников; рассматривается одна из важнейших теорем в геометрии — теорема о сумме углов треугольника, которая позволяет дать классификацию треугольников по углам (остроугольный, прямоугольный, тупоугольный).
На протяжении занятий, особенно при переходе от одной части занятия к другой, смене деятельности встает вопрос о поддержании интереса к занятиям. Таким образом, актуальным
становится вопрос о применении на занятиях по геометрии задач, в которых есть условие проблемной ситуации и элементы творчества . Таким образом, целью
данного исследования является систематизация заданий геометрического содержания с элементами творчества и проблемных ситуаций.
Объект исследования
: Задачи по геометрии с элементами творчества, занимательности и проблемных ситуаций.
Задачи исследования:
Проанализировать существующие задачи по геометрии, направленные на развитие логики, воображения и творческого мышления. Показать, как занимательными приемами можно развить интерес к предмету.
Теоретическая и практическая значимость исследования
состоит в том, что собранный материал может быть использован в процессе дополнительных занятий по геометрии, а именно на олимпиадах и конкурсах по геометрии.
Объем и структура исследования:
Исследование состоит из введения, двух глав, заключения, библиографического списка, содержит 14 страниц основного машинописного текста, 1 таблицу, 10 рисунков.
Глава 1. ПЛОСКИЕ ГЕОМЕТРИЧЕСКИЕ ФИГУРЫ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1. Основные геометрические фигуры в архитектуре зданий и сооружений
В окружающем нас мире существует множество материальных предметов разных форм и размеров: жилые дома, детали машин, книги, украшения, игрушки и т. д.
В геометрии вместо слова предмет говорят геометрическая фигура, при этом разделяя геометрические фигуры на плоские и пространственные. В данной работе будет рассмотрен один из интереснейших разделов геометрии — планиметрия, в которой рассматриваются только плоские фигуры. Планиметрия
(от лат. planum — «плоскость», др.-греч. μετρεω — «измеряю») — раздел евклидовой геометрии, изучающий двумерные (одноплоскостные) фигуры, то есть фигуры, которые можно расположить в пределах одной плоскости. Плоской геометрической фигурой называется такая, все точки которой лежат на одной плоскости. Представление о такой фигуре даёт любой рисунок, сделанный на листе бумаги.
Но прежде, чем рассматривать плоские фигуры, необходимо познакомиться с простыми, но очень важными фигурами, без которых плоские фигуры просто не могут существовать.
Самой простой геометрической фигурой является точка.
Это одна из главных фигур геометрии. Она очень маленькая, но ее всегда используют для построения различных форм на плоскости. Точка — это основная фигура для абсолютно всех построений, даже самой высокой сложности. С точки зрения математики точка — это абстрактный пространственный объект, не обладающий такими характеристиками, как площадь, объем, но при этом остающийся фундаментальным понятием в геометрии.
Прямая
— одно из фундаментальных понятий геометрии.При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии (евклидовой). Если основой построения геометрии служит понятие расстояния между двумя точками пространства, то прямую линию можно определить, как линию, путь вдоль которой равен расстоянию между двумя точками.
Прямые в пространстве могут занимать различные положения, рассмотрим некоторые из них и приведем примеры, встречающиеся в архитектурном облике зданий и сооружений (табл. 1):
Таблица 1
Параллельные прямые | Свойства параллельных прямых | |
Если прямые параллельны, то их одноименные проекции параллельны: | Ессентуки, здание грязелечебницы (фото автора) | |
Пересекающиеся прямые | Свойства пересекающихся прямых | Примеры в архитектуре зданий и сооружений |
Пересекающиеся прямые имеют общую точку, то есть точки пересечения их одноименных проекций лежат на общей линии связи: | Здания «горы» на Тайване https://www.sro-ps.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane | |
Скрещивающиеся прямые | Свойства скрещивающихся прямых | Примеры в архитектуре зданий и сооружений |
Прямые, не лежащие в одной плоскости и не параллельные между собой, являются скрещивающимися. Ноне является общей линией связи. Если пересекающиеся и параллельные прямые лежат в одной плоскости, то скрещивающиеся прямые лежат в двух параллельных плоскостях. | Робер, Гюбер — Вилла Мадама под Римом https://gallerix.ru/album/Hermitage-10/pic/glrx-172894287 |
1.2. Плоские геометрические фигуры. Свойства и определения
Наблюдая за формами растений и животных, гор и извилинами рек, за особенностями ландшафта и далекими планетами, человек заимствовал у природы ее правильные формы, размеры и свойства. Материальные потребности побуждали человека строить жилища, изготавливать орудия труда и охоты, лепить из глины посуду и прочее. Все это постепенно способствовало тому, что человек пришел к осознанию основных геометрических понятий.
Четырехугольники:
Параллелограмм
(др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — черта, линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Признаки параллелограмма:
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий: 1. Если в четырёхугольнике противоположные стороны попарно равны, то четырёхугольник — параллелограмм. 2. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник — параллелограмм. 3. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник — параллелограмм.
Параллелограмм, у которого все углы прямые, называется прямоугольником.
Параллелограмм, у которого все стороны равны, называется ромбом.
Трапеция—
это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны. Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.
Треугольник
— это простейшая геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника
, а отрезки — сторонами треугольника.
Именно в силу своей простоты треугольник явился основой многих измерений. Землемеры при своих вычислениях площадей земельных участков и астрономы при нахождении расстояний до планет и звезд используют свойства треугольников. Так возникла наука тригонометрия — наука об измерении треугольников, о выражении сторон через его углы. Через площадь треугольника выражается площадь любого многоугольника: достаточно разбить этот многоугольник на треугольники, вычислить их площади и сложить результаты. Правда, верную формулу для площади треугольника удалось найти не сразу.
Особенно активно свойства треугольника исследовались в XV-XVI веках. Вот одна из красивейших теорем того времени, принадлежащая Леонарду Эйлеру:
Огромное количество работ по геометрии треугольника, проведенное в XY-XIX веках, создало впечатление, что о треугольнике уже известно все.
Многоуго́льник —
это геометрическая фигура, обычно определяемая как замкнутая ломаная.
Круг
— геометрическое место точек плоскости, расстояние от которых до заданной точки, называемой центром круга, не превышает заданного неотрицательного числа, называемого радиусом этого круга. Если радиус равен нулю, то круг вырождается в точку.
Существует большое количество геометрических фигур, все они отличаются параметрами и свойствами, порой удивляя своими формами.
Чтобы лучше запомнить и отличать плоские фигуры по свойствам и признакам, я придумал геометрическую сказку, которую хотел бы представит вашему вниманию в следующем параграфе.
Глава 2. ЗАДАЧИ-ГОЛОВОЛОМКИ ИЗ ПЛОСКИХ ГЕОМЕТРИЧЕСКИХ ФИГУР
2.1.Головоломки на построение сложной фигуры из набора плоских геометрических элементов.
Изучив плоские фигуры, я задумался, а существуют какие-нибудь интересные задачи с плоскими фигурами, которые можно использовать в качестве заданий-игр или заданий-головоломок. И первой задачей, которую я нашел, была головоломка «Танграм».
Это китайская головоломка. В Китае ее называют «чи тао ту», т.е умственная головоломка из семи частей. В Европе название «Танграм» возникло, вероятнее всего, от слова «тань», что означает «китаец» и корня «грамма» (греч. — «буква»).
Для начала необходимо начертить квадрат 10 х10 и разделить его на семь частей: пять треугольников 1-5
, квадрат 6
и параллелограмм 7
. Суть головоломки состоит в том, чтобы, используя все семь частей, сложить фигурки, показанные на рис.3.
Рис.3. Элементы игры «Танграм» и геометрические фигуры
Рис.4. Задания «Танграм»
Особенно интересно составлять из плоских фигур «образные» многоугольники, зная лишь очертания предметов (рис.4). Несколько таких заданий-очертаний я придумал сам и показал эти задания своим одноклассникам, которые с удовольствием принялись разгадывать задания и составили много интересных фигур-многогранников, похожих на очертания предметов окружающего нас мира.
Для развития воображения можно использовать и такие формы занимательных головоломок, как задачи на разрезание и воспроизведение заданных фигур.
Пример 2. Задачи на разрезание (паркетирование) могут показаться, на первый взгляд, весьма многообразными. Однако в большинстве в них используется всего лишь несколько основных типов разрезаний (как правило, те, с помощью которых из одного параллелограмма можно получить другой).
Рассмотрим некоторые приёмы разрезаний. При этом разрезанные фигуры будем называть многоугольниками.
Рис. 5. Приёмы разрезаний
На рис.5 представлены геометрические фигуры, из которых можно собрать различные орнаментальные композиции и составить орнамент своими руками.
Пример 3. Еще одна интересная задача, которую можно самостоятельно придумать и обмениваться с другими учениками, при этом кто больше соберет разрезанные фигуры, тот объявляется победителем. Задач такого типа может быть достаточно много. Для кодирования можно взять все существующие геометрические фигуры, которые разрезаются на три или четыре части.
Рис.6.Примеры задач на разрезание:
—— —
воссозданный квадрат; — разрез ножницами;
Основная фигура
2.2.Равновеликие и равносоставленные фигуры
Рассмотрим еще один интересный прием на разрезание плоских фигур, где основными «героями» разрезаний будут многоугольники. При вычислении площадей многоугольников используется простой прием, называемый методом разбиения.
Вообще многоугольники называются равносоставленными, если, определенным образом разрезав многоугольник F
на конечное число частей, можно, располагая эти части иначе, составить из них многоугольник Н.
Отсюда вытекает следующая теорема:
равносоставленные многоугольники имеют одинаковую площадь, поэтому они будут считаться равновеликими.
На примере равносоставленных многоугольников можно рассмотреть и такое интересное разрезание, как преобразование «греческого креста» в квадрат (рис.7).
Рис.7. Преобразование «греческого креста»
В случае мозаики (паркета), составленной из греческих крестов, параллелограмм периодов представляет собой квадрат. Мы можем решить задачу, накладывая мозаику, составленную из квадратов, на мозаику, образованную с помощью крестов, так, чтобы при этом конгруэнтные точки одной мозаики совпали с конгруэнтными точками другой (рис.8).
На рисунке конгруэнтные точки мозаики из крестов, а именно центры крестов, совпадают с конгруэнтными точками «квадратной» мозаики — вершинами квадратов. Параллельно сдвинув квадратную мозаику, мы всегда получим решение задачи. Причем, задача имеет несколько вариантов решений, если при составлении орнамента паркета используется цвет.
Рис.8. Паркет, собранный из греческого креста
Еще один пример равносоставленных фигур можно рассмотреть на примере параллелограмма. Например, параллелограмм равносоставлен с прямоугольником (рис.9).
Этот пример иллюстрирует метод разбиения, состоящий в том, что для вычисления площади многоугольника пытаются разбить его на конечное число частей таким образом, чтобы из этих частей можно было составить более простой многоугольник, площадь которого нам уже известна.
Например, треугольник равносоставлен с параллелограммом, имеющим то же основание и вдвое меньшую высоту. Из этого положения легко выводится формула площади треугольника.
Отметим, что для приведенной выше теоремы справедлива и обратная теорема:
если два многоугольника равновелики, то они равносоставлены.
Эту теорему, доказанную в первой половине XIX в. венгерским математиком Ф.Бойяи и немецким офицером и любителем математики П.Гервином, можно представить и в таком виде: если имеется торт в форме многоугольника и многоугольная коробка, совершенно другой формы, но той же площади, то можно так разрезать торт на конечное число кусков (не переворачивая их кремом вниз), что их удастся уложить в эту коробку.
Заключение
В заключении отмечу, что задач на плоские фигуры достаточно представлено в различных источниках, но интерес представили для меня те, на основании которых мне пришлось придумывать свои задачи-головоломки.
Ведь решая такие задачи, можно не просто накопить жизненный опыт, но и приобрести новые знания и умения.
В головоломках при построении действий-ходов используя повороты, сдвиги, переносы на плоскости или их композиции, у меня получились самостоятельно созданные новые образы, например, фигурки-многогранники из игры «Танграм».
Известно, что основным критерием подвижности мышления человека является способность путём воссоздающего и творческого воображения выполнить в установленный отрезок времени определенные действия, а в нашем случае — ходы фигур на плоскости. Поэтому изучение математики и, в частности, геометрии в школе даст мне еще больше знаний, чтобы в дальнейшем применить их в своей будущей профессиональной деятельности.
Библиографический список
1. Павлова, Л.В. Нетрадиционные подходы к обучению черчению: учебное пособие/ Л.В. Павлова. — Нижний Новгород: Изд-во НГТУ, 2002. — 73 с.
2. Энциклопедический словарь юного математика /Сост. А.П. Савин. — М.: Педагогика, 1985. — 352 с.
3.https://www.srops.ru/novosti_otrasli/2015_11_11_pervoe_zdanie_iz_grandioznogo_proekta_big_v_tayvane
4.https://www.votpusk.ru/country/dostoprim_info.asp?ID=16053
Приложение 1
Анкета-опросник для одноклассников
1. Знаете ли вы, что такое головоломка «Танграм»?
2. Что такое «греческий крест»?
3. Было бы вам интересно узнать, что такое «Танграм»?
4. Было бы вам интересно узнать, что такое «греческий крест»?
Было опрошено 22 ученика 8 класса. Результаты: 22 ученика не знают, что такое «Танграм» и «греческий крест». 20-ти ученикам было бы интересно узнать о том, как с помощью головоломки «Танграм», состоящая из семи плоских фигур, получить более сложную фигуру. Результаты опроса обобщены на диаграмме.
Приложение 2
Элементы игры «Танграм» и геометрические фигуры
Преобразование «греческого креста»
Геометрическая фигура
— множество точек на поверхности (зачастую на плоскости), которое образует конечное количество линий.
Основными геометрическими фигурами на плоскости являются точка
и прямая
линия
. Отрезок, луч, ломаная линия — самые простые геометрические фигуры на плоскости.
Точка
— мельчайшая геометрическая фигура, являющаяся основой других фигур во всяком изображении либо чертеже.
Каждая более сложная геометрическая фигура
есть множество точек, которые обладают определенным свойством, характерное только для этой фигуры.
Прямая линия
, либо прямая —
это бесконечное множество точек, расположенных на 1-ой линии, которая не имеет начала и конца. На листе бумаги можно увидеть лишь часть прямой линии, т.к. она не имеет предела.
Прямую изображают так:
Часть прямой линии, которая ограничена с 2-х сторон точками, называют отрезком
прямой, либо отрезком. Его изображают так:
Луч
— это направленная полупрямая, имеющая точку начала и у которой нет конца. Луч изображают так:
Если на прямой поставить точку, то эта точка будет разбивать прямую на 2 противоположно направленных луча. Эти лучи называют дополнительными
.
Ломаная линия
— несколько отрезков, которые соединены друг с другом таким образом, что конец 1-го отрезка оказывается началом 2-го отрезка, а конец 2-го отрезка — началом 3-го отрезка и так далее, причем соседние (которые имеют 1-ну общую точку) отрезки располагаются на разных прямых. Когда конец последнего отрезка не совпадает с началом 1-го, значит, эта ломаная линия будет называться незамкнутой
:
Когда конец последнего отрезка ломаной совпадает с началом 1-го, значит, эта ломаная линия будет замкнутой
. Пример замкнутой ломаной — это всякий многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник (прямоугольник) :
Трехзвенная замкнутая ломаная линия —
учим плоские и объемные геометрические фигуры
Масару Ибука в своей книге «После трёх уже поздно» утверждает, что в первые три года жизни у ребенка самый высокий потенциал к обучению и развитию, поэтому бездействие сродни преступлению.
Конечно, нам может казаться, что ребенок слишком мал. Да и чему он может научиться, если не умеет даже говорить? Но мозг ребёнка, как губка, впитывает всю окружающую его информацию. И от родителей зависит, что усвоит ребенок в этом возрасте.
Стоит ли начинать изучать геометрические фигуры в столь раннем возрасте? Безусловно. Ребенок живет в окружении геометрических форм. Знания, которые вы даёте, не должны быть оторваны от вашей повседневной жизни. Мама – проводник малыша в этом мире, и ей совершенно не обязательно иметь ученую степень, чтобы рассказать ребенку, как устроен мир.
Зачем ребенку учить геометрические фигуры?
Первые три года жизни ребенка – это период развития мозговых клеток, когда образуется прочная база для новых свершений. Уже в 3-4 месяца малыш способен различать формы. Это не означает, что пришла пора заучивать названия геометрических фигур, но мама при разговоре с крохой может стараться употреблять фразы: «А вот и наше любимое круглое блюдце», «Давай посмотрим, что в квадратной коробке» и подобные.
Знание геометрических фигур помогает:
- развивать пространственное мышление, ориентацию в пространстве;
- расширять кругозор;
- развивать способность сравнивать, анализировать, обобщать и выделять главное, классифицировать;
- пополнять словарный запас.
И, конечно же, полученные дошкольником знания послужат ему отличным подспорьем в изучении математики в школе.
Как учить геометрические фигуры с дошкольником?
- Обучение для дошкольников должно строиться в виде увлекательной игры.
- Не нужно ругать ребенка, если он не запомнил названия фигур с 1 раза, даже если с 31 – не стоит.
- Не забывайте органично вплетать геометрические познания в жизнь: «подай квадратную коробочку», «возьми яблоко с круглой тарелки».
- По дороге в сад ищите предметы прямоугольной или круглой формы, соревнуйтесь, кто больше найдет и назовет.
- В игровом арсенале у вас должны быть игрушки правильной геометрической формы — мячи, кубики, детали конструктора.
- Обычно малыши любят помогать маме на кухне. Приобретите круглые, квадратные, прямоугольные формочки и испеките съедобные геометрические фигуры.
- Важно при изучении фигур задействовать и тактильную память. Ребенку гораздо интереснее будет не только увидеть, но и пощупать, погладить, а может еще и лизнуть объект изучения.
- Нагружайте мозг ребёнка дозировано, постепенно дополняя информацией. Например, при изучении фигур повторяйте ещё и цвета: «Смотри, какой синий овал получился».
Основные техники и методики запоминания фигур
Есть немало техник и методик, которые сделают запоминание фигур интересным для детей. Подбор методик будет зависеть от возраста и познаний ребёнка.
- До достижения 1,5 лет проговариваем вслух окружающие предметы, снабжая свой рассказ информацией о форме (давай возьмем круглое яблоко).
- В возрасте 1,5 — 2 лет пользуемся картинками, раскрашиваем фигуры, используем сортеры для изучения фигур. Начинаем с самого простого — круга. Остальные фигуры будем подключать только после того, как ребенок усвоил понятие «круг».
- С 2 лет до достижения школьного возраста можем применять все существующие методики, следуя от простого к сложному.
При изучении геометрических фигур, важно действовать поэтапно. Начать следует с легких фигур: круг, квадрат, треугольник, ромб, прямоугольник, овал. Знания этих фигур доступны для детей 2-3 лет.
Детки постарше, 4-5 лет, включают в свой лексикон и берут в оборот представления об трапеции, параллелограмме, пентагоне, гексагоне, октагоне, декагоне и других многоугольниках. Они уже умеют анализировать, поэтому с легкостью сравнивают и находят отличия между фигурами.
Старшие дошколята знакомятся с объемными фигурами: цилиндр, пирамида, куб, шар, конус, призма.
Разберем некоторые варианты техник по изучению геометрических фигур:
1. Сортер – ищем «домик» для каждой фигуры. Ребенок не только запомнит фигуры, но и будет развивать мелкую моторику вкупе с мышлением.
2. Лепка. Лепите вместе с малышом геометрические фигуры – лучшего занятия для развития мелкой моторики рук и усидчивости просто не придумаешь.
3. Объемные наклейки и магниты, изображающие геометрические фигуры, тоже могут помочь ребенку закрепить в памяти названия фигур.
4. Ищем половинки. Разрежьте геометрические фигуры на две части, смешайте и предложите малышу найти вторую половину.
5. Аппликации. Также из вырезанных фигур можно составлять геометрическую аппликацию. Например, домик (квадрат + треугольник), ёлочку, машинку.
6. Обводить пунктирные геометрические фигуры.
7. Раскрасить или заштриховать предложенные вами геометрические фигуры.
7. Дорисовать фигуру по образцу.
8. Рисовать фигуры при помощи трафаретов.
9. Послушать сказку, где главные герои — геометрические фигуры, а потом зарисовать услышанное.
10. Положить в непрозрачный мешок фигуры разной формы и предложить на ощупь угадать форму предмета.
11. Отличная игра для развития памяти и внимательности. Взрослый готовит вырезанные фигуры разных цветов и размеров и выкладывает перед малышом. Они обсуждают цвета, называют фигуры, а после взрослый прячет фигуру. Задача ребенка обнаружить и назвать, какой фигуры нет.
12. Выкладывание геометрических фигур при помощи счетных палочек или спичек. Когда ребенок овладеет этим навыком, можно перейти на более сложный уровень — решать задачки. Например, убери одну спичку так, чтобы получился треугольник.
13. Ассоциации. Предложите ребенку назвать предметы, на которые похож круг или прямоугольник.
14. Шнуровки и различные рамки-вкладыши, например, квадраты Никитина, где нужно из нескольких предметов воссоздать квадрат, либо доски Сегена, где необходимо вставить недостающую деталь.
15. Подвижные игры. Например, на асфальте рисуются овал, треугольник, квадрат, прямоугольник. По команде взрослого ребенок должен найти названную фигуру и встать в неё.
16. Видеоматериалы. Существует большое количество мультфильмов и обучающих материалов про геометрические фигуры. Посмотрите видео с малышом и обязательно обсудите увиденное.
17. Найдите в интернете и распечатайте картины, которые художники рисуют геометрическими формами, и предложите ребенку посчитать, сколько здесь кругов, прямоугольников и т. д.
Учим объемные геометрические фигуры
Объемные фигуры можно изучать по аналогии с окружающим предметами (например, мяч = шар). И, конечно же, задействовать изучение предмета через игры:
- Найти объемную фигуру по плоскому образцу — отличное упражнение на развитие пространственного мышления.
- «Сыщик». Детям раздают «ориентировку» – плоский рисунок искомой фигуры со всех сторон. Детям необходимо сопоставить картинки и найти нужную фигуру.
- Создать трехмерную модель самому. Взрослый может распечатать трафареты с интернета. Ребенку остается согнуть по линиям и склеить, чтобы получилась фигура.
- Макеты, оригами – можно попробовать с вместе с ребенком создать свою объемную игрушку из бумаги.
- Конструктор. Постройте при помощи деталей башню или замок для принцессы. Эта игра будет способствовать развитию мелкой моторики, воображению, пониманию свойств объемных фигур.
Изучение геометрических фигур не должно становиться пыткой для ребенка и взрослого. Выбирайте ту методику, которая подходит именно вам. Проявите терпение и изобретательность, и тогда результат не заставит себя долго ждать. Главное, не забывайте поощрять ребенка за его новые открытия и время от времени повторять полученные знания.
Математика и логика для детей 7-13 лет
Развиваем логическое мышление через решение сюжетных математических задач в интерактивном игровом формате
узнать подробнее
Называются все фигуры. Плоские и объемные геометрические фигуры
Раиса Баландина
«Объемные геометрические фигуры»
Конспект НОД в подготовительной группе на тему
:
«Объемные геометрические фигуры
»
.
Задачи
:
Упражнять в счёте в пределах 20 в прямом и обратном порядке
Закрепить знания о последовательности дней недели, времён года
Закрепить представления детей о геометрических фигурах
НОД занятия.
Ребята, посмотрите, сегодня утром я шла в детский сад и встретила почтальона. Он мне дал вот такое интересное письмо. Его прислал Буратино. Он уже ходит в школу. Вот,что он пишет
:
«Дорогие ребята! Для того чтобы хорошо учиться в школе, надо много знать, уметь, думать, догадываться. А также решать необычные задачи, выполнять задания на смекалку и сообразительность. Вот мне и задали такие задания, а я затрудняюсь их выполнить. Помогите мне, пожалуйста».
Ребята, давайте поможем Буратино.
1 задание.Ответьте на вопросы
:
Какое время года сейчас? (Весна)
Назовите весенние месяцы
Какой месяц сейчас идёт? (март)
Сколько дней в недели? (семь)
Назови их;
Какой сегодня день недели? (вторник)
Какой четверг по счету? (четвертый)
Вчера какой был день недели?
Завтра какой будет день недели?
2 задание.
Ребята, Буратино, не может выполнить следующее задание.Давайте ему поможем
:
Какой бывает счет? (прямой и обратный)
Считай от 10 до 20;
Считай от 20 обратно;
Назови число меньше пятнадцати;
Назови соседа 11 и 14;
Сравни числа 16 и 18;
Сравни числа 15 и 15;
3 задание.
Воспитатель
: А сейчас мы будем работать с карточкой, которую прислал Буратино. Вы должны рассказать, где и как расположены фигуры
.
Воспитатель
: — Где находиться прямоугольник?
Ребенок
: — Прямоугольник находится посередине.
Воспитатель
: — Где находится овал?
Ребенок
: — Овал находится справа от прямоугольника
Воспитатель
: — Где находится круг?
Ребенок
: — Круг находится внизу, под прямоугольником
Воспитатель
: — Где находится квадрат?
Ребенок
: — Квадрат находится слева от прямоугольника
Воспитатель
: — Где находится треугольник?
Ребенок
: — Треугольник находится сверху, над прямоугольником.
Физминутка.
Поработали, ребятки,
А теперь все на зарядку!
Столько раз ногою топнем (показываю цифру 6)
Столько раз руками хлопнем (показываю цифру 10)
Мы присядем столько раз (показываю цифру 7)
Мы наклонимся сейчас (показываю цифру 4)
Мы подпрыгнем ровно столько (показываю цифру 8)
Ай да счёт! Игра и только.
4 задание.
На столе перед детьми расположены объёмные геометрические фигуры
(шар, куб, цилиндр, конус)
— Следующее задание
: Дети что это? Какие фигуры
? Сколько их? Какая фигура стоит первой
? Второй? Третьей? Какая стоит последней?
Воспитатель
: Ребята, а вы знаете, что геометрические фигуры можно нарисовать
, начертить в тетради, вырезать из цветной бумаги. А еще их можно выложить из счетных палочек. И не одну, а сразу несколько. Давайте попробуем.
А)- отсчитайте три палочки и сделайте треугольник
Отсчитайте еще две палочки и сделайте еще один треугольник
Сколько треугольников получилось? (два)
Сколько палочек вы отсчитали?
Б)- отсчитайте четыре палочки и сделайте квадрат.
Отсчитайте еще три палочки и сделайте еще один квадрат
Какая фигура у вас получилась
? (прямоугольник)
Сколько четырехугольников получилось? (три)
А сколько многоугольников получилось? (три)
Назовите их (два квадрата и один многоугольник)
На какие делятся геометрические фигуры
? (объёмные и плоские)
Чем они отличаются друг от друга? (плоские можно расположить на плоскости, а объёмные нет)
.
Мы сейчас с вами выкладывали на столе объемные или плоские фигуры
?
А сейчас мы с вами сделаем из палочек и пластилина фигуру
, которая состоит из нескольких… а чего? Вы узнаете,отгадав загадку
:
Три вершины в нем видны,
Три угла, три стороны,
С ним знаком даже дошкольник
Ведь фигура –
(треугольник)
.
Ребята, как называется фигура
, которая состоит из нескольких треугольников? (пирамида)
Давайте, сделаем из пластилина и счетных палочек пирамиду.
5 задание.
Ребята, Буратино говорит, что вы уже устали — давайте поиграем. Эта игра — испытание «Верно-неверно»
— поможем исправить ошибки, которые Буратино специально кое-где оставил.
Если вы услышите то, что считаете правильным, хлопайте в ладоши, если же то, что не правильно – покачайте головой
Утром солнышко встает; (верно)
По утрам нужно делать зарядку; (верно)
Нельзя умываться по утрам; (неверно)
Днем ярко светит луна; (неверно)
Утром дети идут в детский сад; (верно)
Ночью люди обедают; (неверно)
Вечером вся семья собирается дома; (верно)
В неделе 7 дней; (верно)
За понедельником следует среда; (неверно)
После субботы идет воскресение; (верно)
Перед пятницей стоит четверг; (верно)
Всего 5 времен года; (неверно)
Весна наступает после лета; (неверно)
.
8 задание. А теперь Буратино приготовил вам графический диктант. Вы должны нарисовать один из признаков (явлений весны)
.
Дети, поставьте карандаш на выделенную точку и рисуйте по клеткам.
Посмотрите и сравните получившийся у вас рисунок с образцом.
Молодцы, ребята!
Итог занятия.
Вот и выполнили вы все задания Буратино. Что же мы сегодня нового узнали? Какие задания с вами выполняли? Какие задания были трудными?
Буратино благодарит вас за помощь.
В сегодняшней статье я хотела бы рассказать о том, как легко и увлекательно можно изучать геометрические фигуры с малышом, и зачем вообще в столь раннем возрасте грузить ребенка геометрией. Какие игры будут интересны малышу от 1 года, и какие материалы вам понадобятся для занятий – обо всем этом, читайте в статье. Кроме этого, здесь вы найдете несколько полезных материалов для скачивания.
Зачем изучать геометрические фигуры с малышом?
- Изучение геометрических фигур полезно для общего развития малыша, расширения его знаний об окружающем мире. Если знакомить ребенка с формами в раннем возрасте, в школе ему придется гораздо проще.
Геометрические формы встречаются нам повсюду, их можно разглядеть в большинстве окружающих нас предметов: мяч круглый, стол прямоугольный и т.д. Анализируя сходство окружающих предметов с геометрическими фигурами, ребенок замечательно тренирует ассоциативное и пространственное мышление.
На умении отличать геометрические фигуры основано множество интересных развивающих игр. Это конструирование, игры с , мозаикой, математическим планшетом, и т.п. Поэтому изучение форм в столь раннем возрасте будет способствовать дальнейшему успешному развитию ребенка.
Итак, игры для изучения и закрепления знаний о геометрических фигурах
:
1. Называем геометрические фигуры всегда и везде
Если во время игр или чтения книг вам встречается какая-либо фигура, обязательно обращайте на нее внимание малыша и называйте ее («Посмотри, мячик похож на круг, а кубик – на квадрат»). Даже если вам кажется, что ребенок еще вряд ли запомнит названия фигур, все равно произносите их, и они обязательно отложатся у него в голове. Делать это можно уже до года. Поначалу указывайте только на основные фигуры (квадрат, круг, треугольник), затем, когда поймете, что малыш их усвоил, начинайте изучать и другие фигуры.
2.
Играем в геометрическое лото
Для первых занятий с малышом лучше использовать лото, где всего 3-4 фигуры. Когда малыш хорошо освоит такую игру, постепенно усложняйте поставленную задачу. Также полезно на первое время все фигуры на игровом поле сделать одного цвета и размера. В этом случае ребенок будет ориентироваться только на один признак – форму, другие же характеристики не будут ни отвлекать, ни подсказывать ему.
Накладывать на игровое поле можно как карточки с изображением фигур, так и объемные фигуры. Хорошо с этой целью подойдут блоки Дьенеша
(Ozon
, KoroBoom
), фигурки от сортера, рамки-вкладыша.
Ну и самый нехлопотный вариант — это приобрести готовое лото с геометрическими фигурами
.
3. Играем с сортером
Примерно в возрасте 1 года ребенок начинает замечать, что выбранную им фигурку сортера
(Озон
, Лабиринт
, My-shop
) можно протолкнуть далеко не в каждое отверстие. Поэтому во время игры необходимо акцентировать на этом внимание: «Так, вот у нас круг – сюда он не подходит, сюда не подходит, а куда же подходит?». Поначалу повернуть фигуру под правильным углом малышу может быть тяжеловато, но это не страшно, это вопрос практики. Главное, не забывайте вовремя увлекательного процесса «проталкивания» все время произносить названия фигур, и ребенок незаметно их все запомнит.
Важно! При выборе сортера обратите внимание на то, чтобы там были представлены все основные геометрические фигуры, а не только сердечки и полумесяцы.
4. Играем с рамкой-вкладышем
Понадобится такая рамка-вкладыш
, на которой представлены все основные фигуры. По своей сути игра аналогична сортеру.
Вот еще одна интересная игра на распознавание форм – «» (Лабиринт
, My-shop
). Несмотря на то, что возраст на ней указан 3-5 лет, она будет интересна ребенку 2-х лет и даже чуть раньше.
9. Учим формы по карточкам Домана
На самом деле, я считаю, что этот метод изучения форм самый эффективный. Если вы занимаетесь по , ребенок очень быстро запомнит все фигуры, а вы потратите на это минимум усилий. Однако нужно заметить, что для того, чтобы знания, полученные по карточкам Домана, отложились у малыша в голове, их нужно закреплять посредством других игр
(см. выше). Иначе ребенок быстро забудет все, что вы ему показывали. Поэтому я рекомендую начинать смотреть карточки Домана с геометрическими фигурами примерно в возрасте 1 года, так как в это время малышу становятся интересны сортеры, рамки-вкладыши, рисование, аппликация и т.п. И, изучив формы по картинкам, он сможет использовать полученные знания в этих играх. Кстати, карточки «Геометрические фигуры» можно , а купить ЗДЕСЬ
.
О нашем опыте изучения фигур по карточкам Домана можно почитать .
10. Смотрим развивающие мультфильмы
Ну и, конечно, не помешает просмотр мультфильмов на тему «Геометрические фигуры», сейчас на просторах интернета их можно найти немало. Вот некоторые из них:
Вместо заключения
Очень часто процесс обучения ребенка геометрическим фигурам (да и не только фигурам) воспринимается родителями исключительно как постоянное экзаменирование ребенка, т.е. они пару раз показывают ребенку, например, квадрат, а в дальнейшем же обучение сводится к вопросу «Скажи, какая это фигура?». Такой подход крайне неправильный. Во-первых, потому что как и любой человек, ребенок не слишком любит, когда ему устраивают проверку знаний, и это только отбивает у него охоту заниматься. Во-вторых, прежде чем о чем-то спрашивать малыша, ему нужно очень много раз это объяснить и показать!
Поэтому постарайтесь сводить проверочные вопросы к минимуму. Просто повторяйте и повторяйте изучаемую информацию, будь то названия фигур или чего-то еще. Делайте это во время игр и бесед с малышом. А то, что ребенок все усвоил, вы вскоре и сами увидите без лишних проверок.
Геометрия – точная математическая наука, которая занимается изучением пространственных и других подобных отношений и форм. Но ее часто называют «сухой», поскольку она не способна описать форму многих природных объектов, ведь облака – это не сферы, горы – не конусы, а молнии распространяются не по прямым линиям. Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.
Тем не менее, существует ряд удивительных фигур, которые обычно не изучаются на школьных уроках геометрии, но именно они окружают человека в реальном мире: в природе и архитектуре, головоломках, компьютерных играх и т. д.
Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.
При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными. Его придумал в 1975 г. Бенуа Мандельброт, позаимствовав латинское слово «fractus» (ломанный, дробленный).
Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.
Это одна из самых необыкновенных трехмерных фигур в геометрии, которую легко сделать в домашних условиях. Для этого достаточно взять бумажную полоску, ширина которой в 5-6 раз меньше ее длины, и, перекрутив один из концов на 180°, склеить их между собой.
Если все сделано правильно, то можно проверить самостоятельно ее удивительные свойства:
- Наличие только одной стороны (без разделения на внутреннюю и внешнюю). Это легко проверить, если попробовать закрасить карандашом одну из ее сторон. Независимо от того, в каком месте и направлении будет начато закрашивание, в результате вся лента будет закрашена одним цветом.
- Непрерывность: если вести ручкой линию вдоль всей поверхности, ее конец соединится с начальной точкой без пересечения границ поверхности.
- Двухмерность (связность): при разрезании ленты Мебиуса вдоль она остается цельной, просто получаются новые фигуры (к примеру, при разрезании надвое получится одно кольцо большего размера).
- Отсутствие ориентированности. Путешествие по такой ленте Мебиуса всегда будет бесконечным, оно приведет к начальной точке пути, только в зеркальном отображении.
Лента Мебиуса широко используется в промышленности и науке (в ленточных конвейерах, матричных принтерах, механизмах для заточки и пр.). Кроме этого существует научная гипотеза, по которой сама Вселенная также представляет собой ленту Мебиуса невероятных размеров.
Полимино
Это плоские геометрические фигуры, которые образуются за счет соединения нескольких квадратов равных размеров по их сторонам.
Названия полимино зависят от количества квадратов, из которых они сформированы:
- мономино – 1;
- домино – 2;
- тримино – 3;
- тетрамино – 4 и т. д.
При этом для каждой разновидности существует разное количество типов фигур: у домино 1 тип, у тримино – 3 типа, у гексамино (из 6 квадратов) – 35 типов. Число различный вариаций зависит от количества используемых квадратов, но при этом еще никому из ученых не удалось найти удивительную формулу, которая будет выражать эту зависимость. Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.
Полиамонд
Наряду с полимино, существует еще одна удивительная геометрическая фигура, используемая для составления других фигур – полиамонд. Он представляет собой многоугольник, сформированный из нескольких равносторонних треугольников равного размера.
Название придумал математик Т. О’Бейрн на основании одного из названий ромба в английском языке – диамонд, который можно составить из 2-х равносторонних треугольников. По аналогии, фигуру из 3-х равносторонних треугольников О’Бейрн назвал триамондом, из 4-х – тетриамондом и т. д.
Главным вопросом их существования остается вопрос о возможном количестве полиамондов, которые можно составить из определенного количества треугольников. Применение полиамондов в реальной жизни также аналогично использованию полимино. Это могут быть разного рода головоломки и логические задачи.
Треугольник Рело
Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.
Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:
- сверла Уаттса, которое позволяет сверлить отверстия практически идеальной квадратной формы, только с чуть закругленными краями;
- медиатора, необходимого для игры на музыкальных щипковых инструментах;
- кулачковых механизмов, используемых для создания зигзагообразных швов в швейных машинах, а также немецких часах;
- стрельчатых арок, характерных для готического стиля в архитектуре.
Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:
Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.
Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей». На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.
Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.
Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.
Существует бесконечное множество форм. Формой называют внешнее очертание предмета.
Изучение форм можно начинать с самого раннего детства, обращая внимание своего ребенка на окружающий нас мир, который состоит из фигур (тарелка – круглая, телевизор – прямоугольный).
Уже с двух лет малыш должен знать три простые фигуры – круг, квадрат, треугольник.
Сначала он их должен просто показывать, когда вы это просите. А в три года уже называть их самостоятельно и отличать круг от овала, квадрат от прямоугольника.
Чем больше упражнений на закрепление форм будет выполнено ребенком, тем больше новых фигур он запомнит.
Будущий первоклашка должен знать все простые геометрические фигуры и уметь составлять из них аппликации.
Что мы называем геометрической фигурой?
Геометрическая фигура — это эталон, с помощью которого можно определить форму предмета или его частей.
Фигуры разделяют на две группы: плоские фигуры, объемные фигуры.
Плоскими фигурами мы назовем те фигуры, которые расположены в одной плоскости. К ним относятся круг, овал, треугольник, четырёхугольник (прямоугольник, квадрат, трапеция, ромб, параллелограмм) и всевозможные многоугольники.
К объемным фигурам относят: сфера, куб, цилиндр, конус, пирамида. Это те фигуры, которые имеют высоту, ширину и глубину.
Следуйте двум простым советам при объяснении геометрических фигур:
- Терпение. То, что нам, взрослым, кажется простым и логичным ребенку покажется просто непонятным.
- Попробуйте рисовать фигуры вместе с ребенком.
- Игра. Начинайте изучать фигуры в игровой форме. Хорошие упражнения для закрепления и изучения плоских форм – аппликации из геометрических фигур. Для объемных – можно использовать готовые покупные игры, а также выбирать аппликации, где можно вырезать и склеивать объемную форму.
Цели урока
:
- Познавательная
: создать условия для ознакомления с понятиями плоские
и объёмные геометрические фигуры,
расширить представление о видах объёмных фигур, научить определять вид фигуры, сравнивать фигуры. - Коммуникативная
: создать условия для формирования умения работать в парах, группах; воспитание доброжелательного отношения друг к другу; воспитывать у учащихся взаимопомощь, взаимовыручку. - Регулятивная
: создать условия для формирования планировать учебную задачу, выстраивать последовательность необходимых операций, корректировать свою деятельность. - Личностная
: создать условия для развития вычислительных навыков, логического мышления, интереса к математике, формирования познавательных интересов, интеллектуальных способностей учащихся, самостоятельность в приобретении новых знаний и практических умений.
Планируемые результаты:
личностные:
- формирование познавательных интересов, интеллектуальных способностей учащихся; формирование ценностных отношений друг к другу;
самостоятельность в приобретении новых знаний и практических умений; - формирование умений воспринимать, перерабатывать полученную информацию, выделять основное содержание.
метапредметные:
- овладение навыками самостоятельного приобретения новых знаний;
- организация учебной деятельности, планирования;
- развитие теоретического мышления на основе формирования умений устанавливать факты.
предметные:
- усвоить понятия плоские и объёмные фигуры, научиться сравнивать фигуры, находить плоские и объёмные фигуры в окружающей действительности, научиться работать с развёрткой.
УУД общенаучные
:
- поиск и выделение необходимой информации;
- применение методов информационного поиска, осознанное и произвольное построение речевого высказывания в устной форме.
УУД личностные
:
- оценивать свои и чужие поступки;
- проявление доверия, внимательности, доброжелательности;
- умение работать в паре;
- выражать положительное отношение к процессу познания.
Оборудование
: учебник, интерактивная доска, смайлики, модели фигур, развёртки фигур, светофоры индивидуальные, прямоугольники -средства обратной связи, Толковый словарь.
Тип урока
: изучение нового материала.
Методы
: словесные, исследовательские, наглядные, практические.
Формы работы
: фронтальная, групповая, парная, индивидуальная.
1. Организация начала урока.
Утром солнышко взошло.
Новый день нам принесло.
Сильными и добрыми
Новый день встречаем мы.
Вот мои руки, я раскрываю
Их навстречу солнцу.
Вот мои ноги, они твердо
Стоят на земле и ведут
Меня верной дорогой.
Вот моя душа, я раскрываю
Её навстречу людям.
Наступи, новый день!
Здравствуй, новый день!
2. Актуализация знаний.
Создадим хорошее настроение. Улыбнитесь мне и друг другу, садитесь!
Чтобы дойти до цели, надо прежде всего идти.
Перед вами высказывание, прочитайте. Что означает это высказывание?
(Чтобы чего-то добиться, нужно что-то делать)
И действительно, ребята, попадающим в цель может стать только тот, кто настраивает себя на собранность и организованность своих действий. И вот я надеюсь, что мы с вами на уроке достигнем своей цели.
Начнем наш путь к достижению цели сегодняшнего урока.
3. Подготовительная работа.
Посмотрите на экран. Что вы видите? (Геометрические фигуры)
Назовите эти фигуры.
Какое задание, вы можете предложить своим одноклассникам? (разделите фигуры на группы)
У вас на партах лежат карточки с этими фигурами. Выполните это задание в парах.
По какому признаку вы разделили эти фигуры?
- Плоские и объемные фигуры
- По основаниям объемных фигур
С какими фигурами мы уже работали? Что учились находить у них? Какие фигуры встречаются нам на геометрии впервые?
Какая же тема нашего урока? (Учитель добавляет слова на доске: объёмные, на доске появляется тема урока: Объёмные геометрические фигуры.)
Чему мы должны научиться на уроке?
4. «Открытие» нового знания в практической исследовательской работе.
(Учитель показывает куб и квадрат.)
Чем они похожи?
Можно ли сказать, что это одно и тоже?
Чем же отличается куб от квадрата?
Давайте проведём опыт. (Ученики получают индивидуальные фигуры – куб и квадрат.)
Попробуем приложить квадрат к плоской поверхности порты. Что видим? Он весь (целиком) лёг на поверхность парты? Вплотную?
!
Как назовём фигуру, которую можно целиком расположить на одной плоской поверхности? (Плоской фигурой.)
Можно ли куб полностью (весь) прижать к парте? Проверим.
Можно ли назвать куб плоской фигурой? Почему? Есть ли пространство между рукой и партой?
!
Значит, что мы можем сказать о кубе? (Занимает определённое пространство, является объёмной фигурой.)
ВЫВОДЫ: Чем же отличаются плоские и объёмные фигуры? (Учитель вывешивает на доске выводы.)
- Можно целиком расположить на одной плоской поверхности.
ОБЪЁМНЫЕ
- занимают определённое пространство,
- возвышаются над плоской поверхностью.
Объёмные фигуры:
пирамида, куб, цилиндр, конус, шар, параллелепипед.
4. Открытие новых знаний.
1. Назовите фигуры, изображенные на рисунке.
Какую форму имеют основания этих фигур?
Какие еще формы можно увидеть на поверхности куба и призмы?
2. Фигуры и линии на поверхности объемных фигур имеют свои названия.
Предложите свои названия.
Боковые стороны, образующие плоскую фигуру называются гранями. А боковые линии – рёбра. Углы многоугольников – вершины. Это элементы объемных фигур.
Ребята, а как вы думаете, как называются такие объемные фигуры, у которых много граней? Многогранники.
Работа с тетрадями: чтение нового материала
Соотнесение реальных объектов и объёмных тел.
А теперь подберите для каждого предмета ту объёмную фигуру, на которую он похож.
Коробка – параллелепипед.
- Яблоко – шар.
- Пирамидка – пирамида.
- Банка – цилиндр.
- Горшок из-под цветка — конус.
- Колпачок – конус.
- Ваза – цилиндр.
- Мяч – шар.
5. Физминутка.
1. Представьте себе большой шар, погладьте его со всех сторон. Он большой, гладкий.
(Ученики «обхватывают» руками и гладят воображаемый шар.)
А теперь представьте себе конус, дотроньтесь до его вершины. Конус растёт вверх, вот он уже выше вас. Допрыгните до его вершины.
Представьте, что вы внутри цилиндра, похлопайте по его верхнему основанию, потопайте по нижнему, а теперь руками по боковой поверхности.
Цилиндр стал маленькой подарочной коробочкой. Представьте, что вы сюрприз, который находится в этой коробочке. Я нажимаю кнопку и… сюрприз выскакивает из коробочки!
6. Групповая работа
:
(Каждая группа получает одну из фигур: куб, пирамиду, параллелепипед.Полученную фигуру дети изучают, выводы записывают в подготовленную учителем карточку
.)
Группа 1.
(Для изучения параллелепипеда)
Группа 2.
(Для изучения пирамиды)
Группа 3.
(Для изучения куба)
7. Решение кроссворда
8. Итог урока. Рефлексия деятельности.
Решение кроссворда в презентации
Что нового вы для себя сегодня открыли?
Все геометрические фигуры можно разделить на объёмные и плоские.
А я узнал названия объёмных фигур
Плоские и объемные геометрические фигуры.
Тема: «Плоские и объёмные геометрические фигуры»
Цель: совершенствовать знания о геометрических фигурах и форме предметов.
Задачи: совершенствовать умение соотносить цифру с количеством; закреплять умения сравнивать предметы по длине, высоте; закреплять умения ориентироваться на листе бумаги развивать внимание, память, мышление; воспитывать интерес к математике;
Оборудование: картинки «Геометрические деревья», «Геометрическая улица», наборы геометрических фигур, альбомные листы (по колличеству детей), шар, куб; игрушка Старичка – лесовичка; строительный материал, карточки с изображением качели.
Ход занятия:
Мотивация
Организационный момент.
Игра-приветствие «Наши умные головки»
Наши умные головки
Будут думать много, ловко.
Ушки будут слушать,
Ротик четко говорить.
Ручки будут хлопать,
Ножки будут топать.
Спинки выпрямляются,
Друг другу улыбаемся,
Занятие начинается.
Воспитатель: — Внимание, ребята! Хочу вам сообщить, сегодня путешествие хотим мы совершить. Я знаю волшебные слова, которые помогут нам отправиться в путешествие в страну геометрических фигур.
Постановка цели
Воспитатель: Какие геометрические фигуры вы знаете? (ответы детей).
Воспитатель: Круг, овал, треугольник, прямоугольник, квадрат — это плоскостные фигуры. Еще есть фигуры объемные — куб, шар, цилиндр.
В геометрической стране геометрические фигуры везде-везде. А с нами пойдет Старичок – лесовичок, он все тропки в стране геометрических фигур знает. Нам много придется сегодня пройти и много задачек решить по пути. Итак, отправляемся в сказочное путешествие.
«Ножкой топнем – в ладоши хлопнем
Вокруг себя повернемся, дружно за руки возьмемся
Глаза закроем – скажем «АХ» — и окажемся в гостях»
Вот мы и в стране геометрических фигур.
Совместная деятельность воспитателя с детьми
Наш первый привал. А называется он «Трудные задачки».
— На привале посидим, и задачки все решим.
Ребята, садитесь за столы.
Упражнение «Геометрические деревья»
Перед вами карточки, на которых изображены деревья с кронами, похожими на геометрические фигуры. Сосчитайте, сколько всего деревьев на рисунке? (Пять деревьев). Покажите дерево, с кроной похожей на круг (овал, треугольник, прямоугольник, квадрат).
Какое по счету дерево с круглой кроной (овальной, треугольной, прямоугольной, квадратной)?
Воспитатель: — Молодцы, ребята! Вы справились с заданием, и мы отправляемся дальше.
Шли мы, шли, шли мы, шли, на второй привал «Угадай — ка» пришли.
Этот привал находится на улице «Геометрическая».
— Рассмотрите дома геометрической страны.
— Как вы думаете, в каком доме живет какая геометрическая фигура?
— Чей дом самый высокий (низкий)?
— Чей дом самый широкий (узкий)?
— К чьему дому ведет самая длинная (короткая) дорожка?
Самостоятельная деятельность детей
Упражнение «Геометрические качели»
— В стране геометрических фигур есть волшебные качели. На качелях катаются геометрические фигуры. С левой стороны качелей посадите кататься три круга. А на правую сторону посадите квадратов, на один меньше, чем кругов. Что можно сделать, чтобы кругов и квадратов стало поровну? (Добавить один квадрат или убрать один круг.)
Шли мы, шли, шли мы, шли и на третий привал пришли.
Упражнение «Расставь геометрические фигуры на листе»
— А сейчас возьмите с края стола листы бумаги и приготовьте для работы картонные геометрические фигуры.
— Поставь квадрат в правый верхний угол.
— Поставь круг в середину листа.
— Поставьте треугольник в левый нижний угол.
— Поставьте овал в левый верхний угол.
— Поставьте треугольник в правый нижний угол.
— Молодцы ребята, вы отлично справились с заданием.
Динамическая пауза «Сосчитай и сделай»
А сейчас, ребята, давайте немного отдохнем.
Вставайте из-за столов и выходите ко мне.
Нас ждет физкультминутка!
Сколько точек в этом круге (5),
Столько раз поднимем руки.
Сколько палочек до точки (6),
Столько встанем на носочки.
Сколько ёлочек зелёных (4),
Столько сделаем наклонов.
Сколько здесь у нас кружков (7),
Столько сделаем прыжков.
Совместная деятельность воспитателя с детьми.
— В стране геометрических фигур Старичку-лесовичку очень нравится и ему бы хотелось здесь остаться. Он просит, чтобы вы помогли ему построить дом, а для строительства он принес материал. Вот, что он принес (показ строительного материала).
— Поможем построить дом для Старичка-лесовичка? (Ответ детей)
— Какие фигуры подойдут для строительства? Это кубы, они объёмные, у них есть углы, ребра, грани. Одна грань куба – квадрат.
— Чем куб отличается от квадрата? (Квадрат плоский, куб объемный)
— Чем куб отличается от шара? (Есть углы, не может катиться).
— Какое общее свойство у куба и шара? (Они оба объемные)
Воспитатель: — Почему из кубов удобно строить? (Они не катятся, объемные).
— Из каких фигур мы строили дом? (Ответы детей).
— Ребята, а кем были вы во время строительства домов? (Строителями). А кто такие строители? (Ответы детей)
Воспитатель: — Нелегкое дело — строительство дома. Устали вы, наверное, пока строили, давайте немного взбодримся.
Физкультминутка:
— 1, 2, 3, 4, 5 – хотим строителями стать (хлопки, руки в стороны)
Дружно доски поднимаем (руки вверх)
Быстро гвозди забиваем (кулачком об кулачок)
Кистью красим новый дом (поворот вокруг себя, «красят кистью»)
Чтоб уютно было в нём.
1, 2, 3, — дом построен – посмотри! (Прыжки, руки в стороны).
Воспитатель: — Ну как Старичок – лесовичок, ребята построили для вас дом?
— Молодцы, ребята! Старичок-лесовичок благодарит вас за помощь!
— Ну что ж, как не грустно, но нам пора возвращаться домой, все тропинки одолели без запинки.
— Закройте все глаза, а мы сосчитаем обратным счётом от 3 до 1. Вот мы и в группе, но я думаю, что мы ещё не раз побываем в замечательной стране геометрических фигур.
Рефлексия
Вы сегодня побывали в гостях у сказки, где все связано с математикой. Все вы старались, внимательно слушали, поэтому и справились со всеми заданиями.
— Какие задания вам показались интересными? Какие сложными? С какими заданиями вы справились быстрее.
— Занятие закончилось, спасибо Старичку-лесовичку за наше сказочное путешествие!
Автор:
Николаевская М.О.
математических формул для основных фигур и трехмерных фигур
В математике (особенно в геометрии) и естественных науках вам часто нужно вычислять площадь поверхности, объем или периметр различных форм. Будь то сфера или круг, прямоугольник или куб, пирамида или треугольник, каждая форма имеет определенные формулы, которым вы должны следовать, чтобы получить правильные измерения.
Мы собираемся изучить формулы, которые понадобятся вам для определения площади поверхности и объема трехмерных фигур, а также площади и периметра двухмерных фигур.Вы можете изучить этот урок, чтобы изучить каждую формулу, а затем сохранить ее для быстрого ознакомления в следующий раз, когда она вам понадобится. Хорошая новость заключается в том, что в каждой формуле используются одни и те же базовые измерения, поэтому изучение каждого нового становится немного проще.
Площадь и объем сферы
Д. Рассел
Трехмерный круг известен как сфера. Чтобы рассчитать площадь поверхности или объем сферы, вам необходимо знать радиус ( r ). Радиус — это расстояние от центра сферы до края, и оно всегда одинаково, независимо от того, от каких точек на краю сферы вы измеряете.
Когда у вас есть радиус, формулы довольно просто запомнить. Как и в случае с окружностью круга, вам нужно будет использовать число пи ( π ). Как правило, это бесконечное число можно округлить до 3,14 или 3,14159 (принятая дробь — 22/7).
- Площадь поверхности = 4πr 2
- Объем = 4/3 πr 3
Площадь поверхности и объем конуса
Д. Рассел
Конус — это пирамида с круглым основанием, имеющая наклонные стороны, которые сходятся в центральной точке.Чтобы рассчитать его площадь поверхности или объем, необходимо знать радиус основания и длину стороны.
Если вы этого не знаете, вы можете найти длину стороны ( s ), используя радиус ( r ) и высоту конуса ( h ).
После этого вы можете найти общую площадь поверхности, которая является суммой площади основания и площади стороны.
- Площадь основания: πr 2
- Площадь стороны: πrs
- Общая площадь поверхности = πr 2 + πrs
Чтобы найти объем сферы, вам нужны только радиус и высота.
Площадь и объем цилиндра
Д. Рассел
Вы обнаружите, что с цилиндром намного легче работать, чем с конусом. Эта форма имеет круглое основание и прямые параллельные стороны. Это означает, что для определения его площади поверхности или объема вам понадобятся только радиус ( r ) и высота ( h ).
Тем не менее, вы также должны учитывать то, что есть как верх, так и низ, поэтому радиус необходимо умножить на два для площади поверхности.
- Площадь поверхности = 2πr 2 + 2πrh
- Объем = πr 2 ч
Площадь и объем прямоугольной призмы
Д. Рассел
Прямоугольник в трех измерениях становится прямоугольной призмой (или коробкой). Когда все стороны равны, он становится кубом. В любом случае для определения площади поверхности и объема требуются одни и те же формулы.
Для них вам нужно знать длину ( л ), высоту ( х ) и ширину ( х ).С кубом все три будут одинаковыми.
- Площадь поверхности = 2 (слева) + 2 (lw) + 2 (белый)
- Объем = lhw
Площадь и объем пирамиды
Д. Рассел
С пирамидой с квадратным основанием и гранями из равносторонних треугольников работать сравнительно легко.
Вам нужно будет знать размер одной длины основания ( b ). Высота ( х ) — это расстояние от основания до центральной точки пирамиды.Сторона ( s ) — это длина одной грани пирамиды от основания до верхней точки.
- Площадь поверхности = 2bs + b 2
- Объем = 1/3 млрд 2 ч
Другой способ вычислить это — использовать периметр ( P ) и площадь ( A ) базовой формы. Это можно использовать для пирамиды с прямоугольным, а не квадратным основанием.
- Площадь поверхности = (½ x P x s) + A
- Объем = 1/3 Ач
Площадь поверхности и объем призмы
Д.Рассел
При переходе от пирамиды к равнобедренной треугольной призме необходимо также учитывать длину формы ( l ). Запомните сокращения для основания ( b ), высоты ( h ) и стороны ( s ), потому что они необходимы для этих расчетов.
- Площадь поверхности = bh + 2ls + lb
- Объем = 1/2 (bh) л
Тем не менее, призма может быть любой формы. Если вам нужно определить площадь или объем нечетной призмы, вы можете полагаться на площадь ( A ) и периметр ( P ) базовой формы.Часто в этой формуле будет использоваться высота призмы или глубина ( d ), а не длина ( l ), хотя вы можете видеть любое сокращение.
- Площадь поверхности = 2A + Pd
- Объем = Ad
Площадь сектора круга
Д. Рассел
Площадь сектора круга может быть вычислена в градусах (или радианах, как это чаще всего используется в расчетах). Для этого вам понадобятся радиус ( r ), пи ( π ) и центральный угол ( θ ).
- Площадь = θ / 2 r 2 (в радианах)
- Площадь = θ / 360 πr 2 (в градусах)
Площадь эллипса
Д. Рассел
Эллипс также называют овалом и по сути представляет собой удлиненный круг. Расстояния от центральной точки до стороны непостоянны, что делает формулу для определения ее площади немного сложной.
Чтобы использовать эту формулу, вы должны знать:
- Semiminor Axis ( a ): кратчайшее расстояние между центральной точкой и краем.
- Большая полуось ( b ): наибольшее расстояние между центральной точкой и краем.
Сумма этих двух точек остается постоянной. Вот почему мы можем использовать следующую формулу для вычисления площади любого эллипса.
Иногда вы можете увидеть эту формулу, записанную как r 1 (радиус 1 или малая полуось) и r 2 (радиус 2 или большая полуось), а не a и b .
Площадь и периметр треугольника
Треугольник — одна из самых простых фигур, и вычислить периметр этой трехсторонней формы довольно просто. Вам необходимо знать длины всех трех сторон ( a, b, c ), чтобы измерить полный периметр.
Чтобы узнать площадь треугольника, вам понадобится только длина основания ( b ) и высота ( h ), которая измеряется от основания до вершины треугольника. Эта формула работает для любого треугольника, независимо от того, равны ли стороны или нет.
Площадь и окружность круга
Подобно сфере, вам нужно знать радиус ( r ) круга, чтобы узнать его диаметр ( d ) и длину окружности ( c ). Имейте в виду, что круг — это эллипс, который имеет одинаковое расстояние от центральной точки до каждой стороны (радиуса), поэтому не имеет значения, где на краю вы измеряете.
- Диаметр (d) = 2r
- Окружность (c) = πd или 2πr
Эти два измерения используются в формуле для вычисления площади круга.Также важно помнить, что отношение длины окружности к ее диаметру равно пи ( π ).
Площадь и периметр параллелограмма
У параллелограмма есть два набора противоположных сторон, идущих параллельно друг другу. Форма четырехугольная, поэтому у нее четыре стороны: две стороны одной длины ( a ) и две стороны другой длины ( b ).
Чтобы узнать периметр любого параллелограмма, используйте эту простую формулу:
Когда вам нужно найти площадь параллелограмма, вам понадобится высота ( х ).Это расстояние между двумя параллельными сторонами. Также требуется основание ( b ) — это длина одной из сторон.
Имейте в виду, что b в формуле площади не то же самое, что b в формуле периметра. Вы можете использовать любую из сторон, которые были соединены как a и b при вычислении периметра, хотя чаще всего мы используем сторону, перпендикулярную высоте.
Площадь и периметр прямоугольника
Прямоугольник — тоже четырехугольник.В отличие от параллелограмма, внутренние углы всегда равны 90 градусам. Кроме того, стороны, противоположные друг другу, всегда будут иметь одинаковую длину.
Чтобы использовать формулы для периметра и площади, вам необходимо измерить длину прямоугольника ( l ) и его ширину ( w ).
- Периметр = 2h + 2w
- Площадь = h x w
Площадь и периметр квадрата
Квадрат даже проще, чем прямоугольник, потому что это прямоугольник с четырьмя равными сторонами.Это означает, что вам нужно знать только длину одной стороны ( s ), чтобы найти ее периметр и площадь.
Площадь и периметр трапеции
Трапеция — это четырехугольник, который может показаться сложной задачей, но на самом деле это довольно просто. У этой формы только две стороны параллельны друг другу, хотя все четыре стороны могут иметь разную длину. Это означает, что вам нужно знать длину каждой стороны ( a, b 1 , b 2 , c ), чтобы найти периметр трапеции.
- Периметр = a + b 1 + b 2 + c
Чтобы найти площадь трапеции, вам также понадобится высота ( х ). Это расстояние между двумя параллельными сторонами.
Площадь и периметр шестиугольника
Шестигранный многоугольник с равными сторонами — это правильный шестиугольник. Длина каждой стороны равна радиусу ( r ). Хотя это может показаться сложной формой, вычисление периметра — это простой вопрос умножения радиуса на шесть сторон.
Определить площадь шестиугольника немного сложнее, и вам придется запомнить эту формулу:
Площадь и периметр восьмиугольника
Правильный восьмиугольник похож на шестиугольник, но у этого многоугольника восемь равных сторон. Чтобы найти периметр и площадь этой формы, вам понадобится длина одной стороны ( a ).
- Периметр = 8a
- Площадь = (2 + 2√2) a 2
Формула площади и объема для геометрических фигур
пи (π) = 3.14155 …
Формула периметра | ||||||
| Квадрат | 4 × сторона | |||||
| Прямоугольник | 2 × (длина + ширина) | |||||
| Параллелограмм | 2 × | сторона1 + сторона2 + сторона3 | ||||
| Правильный n-многоугольник | n × сторона | |||||
| Трапеция | высота × (основание1 + основание2) / 2 | |||||
| Трапеция | + высота csc (theta1) + csc (theta2)] | |||||
| Круг | 2 × pi × радиус | |||||
| Эллипс | 4 × radius1 × E (k, pi / 2) E (k, pi / 2) — полный эллиптический интеграл второго рода k = (1 / radius1) × sqrt (radius1 2 — radius2 2 ) | |||||
Формула площади | ||||||
| Квадрат | сторона 2 | |||||
| Прямоугольник | длина × ширина | |||||
| Параллелограмм | основание × высота | |||||
| Треугольник | основание × высота / 2 | n-образный | n-образный (1/4) × n × сторона 2 × кроватка (pi / n) | |||
| Трапеция | высота × (base1 + base2) / 2 | |||||
| Окружность | pi × радиус 2 | |||||
| Эллипс | пи × радиус1 × радиус2 | |||||
| Куб (поверхность) | 6 × сторона 2 | |||||
| Сфера (поверхность) | 4 × пи × радиус 2 | |||||
| периметр окружности × высота | ||||||
| 2 × pi × радиус × высота | ||||||
| Цилиндр (вся поверхность) | Площади верхней и нижней окружностей + Площадь стороны | |||||
| 2 (пи × радиус 2 ) + 2 × пи × радиус × высота | ||||||
| Конус (поверхность) | пи × радиус × сторона | |||||
| Тор (поверхность) | пи 2 × (радиус2 2 — радиус1 2 ) | |||||
Формула объема | ||||||
| Куб | сторона 3 | |||||
| Прямоугольная призма | сторона1 × сторона 2 × сторона3 | 9039 3) × пи × радиус 3 | ||||
| Эллипсоид | (4/3) × пи × радиус1 × радиус2 × радиус3 | |||||
| Цилиндр | пи × радиус 2 × высота | Конус | (1/3) × pi × радиус 2 × высота | |||
| Пирамида | (1/3) × (площадь основания) × высота | |||||
| Torus | (1/4) × pi 2 × (r1 + r2) × (r1 — r2) 2 | |||||
Источник: Spiegel, Murray R.Математический справочник формул и таблиц.
Серия набросков Шаума по математике. McGraw-Hill Book Co., 1968.
Калькулятор объема
. Определение | Формулы
Калькулятор объема вычислит объем некоторых из наиболее распространенных трехмерных твердых тел. Прежде чем мы перейдем к тому, как рассчитать объем, вы должны знать определение объема. Объем отличается от площади, которая представляет собой объем пространства, занимаемого двухмерной фигурой. Поэтому вы можете быть сбиты с толку относительно того, как найти объем прямоугольника по сравнению с тем, как найти объем коробки.Калькулятор поможет вычислить объем сферы, цилиндра, куба, конуса и прямоугольных тел.
Что такое объем? Определение объема
Объем — это объем пространства, занимаемого объектом или веществом. Как правило, под объемом контейнера понимается его вместимость, а не пространство, которое сам контейнер перемещает. Кубический метр (м 3 ) — это единица измерения объема в системе СИ.
Однако термин том может также относиться ко многим другим вещам, например,
- степень громкости или интенсивность звука (вы можете проверить наш калькулятор шумового загрязнения или калькулятор дБ)
- количество или количество чего-либо (обычно большого количества)
- формальное слово для книги или одной из набора связанных книг.
Единицы объема, таблица пересчета
Популярные единицы объема:
- Метрические единицы объема
- кубических сантиметров (см³)
- кубических метров (м³)
- литров (л, л)
- миллилитры (мл, мл)
- Стандарт США, Великобритания
- жидкая унция (жидкая унция)
- кубический дюйм (у.е.)
- кубических футов
- стаканов
- пинт (пт)
- кварты (кварты)
- галлонов (гал.)
Если вам нужно преобразовать единицы объема, вы можете использовать наш конвертер больших объемов.Еще один полезный инструмент — наш калькулятор граммов в чашки, который может помочь, если вы хотите использовать рецепт еды из другой страны. Обратите внимание, что это не простое преобразование, а переход от веса (граммов) к единице объема (чашки) — поэтому вам нужно знать тип ингредиента (или, точнее, его плотность).
Кроме того, вы можете взглянуть на эту аккуратную таблицу преобразования единиц объема, чтобы узнать коэффициент преобразования в мгновение ока:
| кубических дюймов | кубических футов | кубических ярдов | жидких галлонов сша | американских сухих галлонов | imp жидких галлонов | баррелей (нефть) | чашек | жидких унций (Великобритания) | жидких унций (США) | пинт (Великобритания) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| кубический метр | 6.1 10 4 | 35,3 | 1,30 8 | 264,2 | 227 | 220 | 6,29 | 4227 | 3,52 10 4 | 3,38 10 4 | 1760 |
| кубический дециметр | 61.02 | 0,035 | 1,3 10 -3 | 0,264 | 0,227 | 0,22 | 0,006 | 4,23 | 35,2 | 33,8 | 1,76 |
| кубический сантиметр | 0.061 | 3,5 10 -5 | 1,3 10 -6 | 2,64 10 -4 | 2,27 10 -4 | 2,2 10 -4 | 6,29 10 -6 | 4,2 10 -3 | 3,5 10 -2 | 3.34 10 -2 | 1,76 10 3 |
| кубический миллиметр | 6,1 10 -5 | 3,5 10 -8 | 1,31 10 -9 | 2,64 10 -7 | 2,27 10 -7 | 2,2 10 -7 | 6.3 10 -9 | 4,2 10 -6 | 3,5 10 -5 | 3,4 10 -5 | 1,76 10 -6 |
| гектолитров | 6,1 10 3 | 3,53 | 0,13 | 26.4 | 22,7 | 22 | 0,63 | 423 | 3,5 10 3 | 3381 | 176 |
| литра | 61 | 3,5 10 -2 | 1.3 10 -3 | 0,26 | 0,23 | 0,22 | 6,3 10 -3 | 4,2 | 35,2 | 33,8 | 1,76 |
| сантилитров | 0,61 | 3.5 10 -4 | 1,3 10 -5 | 2,6 10 -3 | 2,3 10 -3 | 2,2 10 -3 | 6,3 10 -5 | 4,2 10 -2 | 0,35 | 0,338 | 1.76 10 -2 |
| миллилитры | 6,1 10 -2 | 3,5 10 -5 | 1,3 10 -6 | 2,6 10 -4 | 2,3 10 -4 | 2,2 10 -4 | 6,3 10 -6 | 4.2 10 -3 | 3,5 10 -2 | 3,4 10 -2 | 1,76 10 -3 |
| куб. Дюймы | 1 | 5,79 10 -4 | 2,1 10 -5 | 4,3 10 -3 | 3.7 10 -3 | 3,6 10 -3 | 10 -4 | 6,9 10 -2 | 0,58 | 0,55 | 2,9 10 -2 |
| кубических футов | 1728 | 1 | 0.037 | 7,48 | 6,43 | 6,23 | 0,18 | 119,7 | 997 | 958 | 49,8 |
| кубических ярдов | 4,7 10 4 | 27 | 1 | 202 | 173.6 | 168,2 | 4,8 | 3232 | 2,69 10 4 | 2,59 10 4 | 1345 |
| галлон жидкого топлива сша | 231 | 0,134 | 4,95 10 -3 | 1 | 0.86 | 0,83 | 0,024 | 16 | 133,2 | 128 | 6,7 |
| галлонов сухих сша | 268,8 | 0,156 | 5,76 10 -3 | 1.16 | 1 | 0,97 | 0,028 | 18,62 | 155 | 148,9 | 7,75 |
| imp жидкие галлоны | 277,4 | 0,16 | 5,9 10 -3 | 1.2 | 1,03 | 1 | 0,029 | 19,2 | 160 | 153,7 | 8 |
| баррели (масло) | 9702 | 5,61 | 0,21 | 42 | 36.1 | 35 | 1 | 672 | 5596 | 5376 | 279,8 |
| чашки | 14,4 | 8,4 10 -3 | 3,1 10 -4 | 6.2 10 -2 | 5,4 10 -2 | 5,2 10 -2 | 1,5 10 -3 | 1 | 8,3 | 8 | 0,4 |
| жидких унций (Великобритания) | 1,73 | 10-3 | 3.7 10 -5 | 7,5 10 -3 | 6,45 10 -3 | 6,25 10 -3 | 1,79 10 -4 | 0,12 | 1 | 0,96 | 5 10 -2 |
| жидких унций (США) | 1.8 | 10 -3 | 3,87 10 -5 | 7,8 10 -3 | 6,7 10 -3 | 6,5 10 -3 | 1,89 10 -4 | 0,13 | 1,04 | 1 | 0.052 |
| пинты (Великобритания) | 34,7 | 0,02 | 7,4 10 -4 | 0,15 | 0,129 | 0,125 | 3,57 10 3 | 2,4 | 20 | 19.2 | 1 |
Как рассчитать объем? Формулы объема
На этот вопрос нет однозначного ответа, так как он зависит от формы рассматриваемого объекта. Вот формулы для некоторых из наиболее распространенных форм:
Куб =
с³, где с — длина стороны.Сфера =
(4/3) πr³, где r — радиус.Цилиндр =
πr²h, где r — радиус, а h — высота.Конус =
(1/3) πr²h, где r — радиус, а h — высота.Прямоугольное тело (объем ящика) =
lwh, где l — длина, w — ширина и h — высота (примером такой формы может служить простой бассейн).Пирамида =
(1/3) Ah, где A — площадь основания, а h — высота. Для пирамиды с правильным основанием можно также использовать другое уравнение: Пирамида =(n / 12) * h * длина_сокры ² * кроватка (π / n), где n — количество сторон основания для правильный многоугольник.Призма =
πAh, где A — площадь основания, а h — высота. Для прямоугольной призмы уравнение можно легко вывести, как и для правой прямоугольной призмы, которая, по-видимому, имеет ту же форму, что и прямоугольник.
| Форма | Имя | Формула |
|---|---|---|
| Куб | В = с³ | |
| Призма прямоугольная правая (прямоугольная, прямоугольная) | V = lwh | |
| Призма или цилиндр | В = Ач | |
| Пирамида или конус | В = Ач / 3 | |
| Сфера | V = 4πr³ / 3 |
Калькулятор объема и инструменты, предназначенные для определенных форм
Мы решили сделать из этого калькулятора объема простой инструмент, охватывающий пять самых популярных трехмерных фигур.Однако не все уравнения объема и формы могут быть реализованы здесь, так как это сделает калькулятор перегруженным и не интуитивно понятным. Так что, если вы ищете конкретную форму, ознакомьтесь с калькуляторами, посвященными объемам выбранных форм:
Калькулятор объема
— как использовать
Давайте посмотрим на примере использования этого калькулятора объема:
Выберите тип 3D-формы . Если вы не можете найти форму, объем которой хотите рассчитать, выберите другие специальные специальные калькуляторы (ссылки вы найдете выше).В этом примере предположим, что вы хотите рассчитать объем цилиндра.
Выберите правую часть калькулятора объема . В нашем случае это деталь под названием Объем цилиндра .
Введите данные в соответствующие поля . Наш цилиндр имеет радиус 1 фут и высоту 3 фута. Вы можете изменить единицы измерения простым щелчком по названию единицы.
Поехали! Отображается объем выбранной формы .В нашем случае это 9,42478 куб. Футов
Если вы хотите проверить, сколько это в баррелях США, просто нажмите на название единицы и выберите бочки из раскрывающегося списка. Наш цилиндр имеет емкость ~ 2,24 баррелей масла.
Измерение объема твердых тел, жидкостей и газов
Как найти объем объектов с разным состоянием материи?
- Цельный
Для обычных трехмерных объектов вы можете легко вычислить объем, измерив его размеры и применив соответствующее уравнение объема.Если это неправильная форма, вы можете попробовать сделать то же самое, что заставило Архимеда выкрикнуть знаменитое слово * Эврика *! Вероятно, вы слышали эту историю — Архимеда попросили выяснить, сделана ли корона Иеро из чистого золота или просто позолочена, но не сгибая и не разрушая ее. Идея пришла ему в голову, когда он принимал ванну — войдя в ванну, он заметил, что уровень воды поднялся. Из этого наблюдения он пришел к выводу, что объем вытесненной воды должен быть равен объему той части его тела, которую он погрузил в воду.Зная объем необычного объекта и его вес, он мог вычислить плотность и сравнить ее с плотностью чистого золота. Легенда гласит, что Архимед был так взволнован этим открытием, что выскочил из ванны и побежал голым по улицам Сиракуз.
Итак, если вы хотите измерить объем необычного объекта, просто следуйте по стопам Архимеда (хотя вы можете опустить часть «голая гонка»):
Возьмите емкость больше, чем объект, объем которого вы хотите измерить .Это может быть ведро, мерный стаканчик, химический стакан или мерный цилиндр. На нем должна быть шкала.
Налейте воду в емкость и снимите показания объема.
Поместите объект внутрь . Он должен быть полностью погружен для измерения всего объема объекта. Прочтите том. Этот метод не сработает, если ваш объект растворяется в воде.
Разница между замерами — это объем нашего объекта.
Эти измерения необходимы для расчета выталкивающей силы, основанной на принципе Архимеда.
- Жидкость
Обычно измерить объем жидкости довольно просто — все, что вам нужно, — это какой-нибудь мерный сосуд с градуировкой. Выберите тот, который соответствует вашим потребностям: необходимо учитывать количество жидкости и степень точности. Емкости, используемые для выпечки торта (посмотрите отличный калькулятор для рецепта блинов), будут отличаться от тех, которые используются в химии (например.грамм. в расчетах молярной концентрации) будет отличаться от тех, которые используются в медицинских целях (например, доза лекарства).
- Газ
Мы должны использовать более сложные методы для измерения объема газа. Вы должны помнить, что на объем газа влияют температура и давление, и что газы расширяются, чтобы заполнить любой контейнер, в который они помещены. Вы можете попробовать измерить это:
Надуйте баллон газом, который вы хотите измерить (например,г., с гелием, чтобы поднять вас в воздух). Затем можно воспользоваться методом Архимеда — опустить баллон в ведро с водой и проверить разницу объемов. Вы найдете подробные инструкции на странице wikihow.
Проверьте показатели, связанные с объемом ваших легких, с помощью прибора под названием спирометр .
В химии, газовый шприц используется для ввода или отбора объема газа из закрытой системы . Эту лабораторную посуду также можно использовать для измерения объема газа, выделяющегося в результате химической реакции.
Или рассчитать :
Найдите объем газа, учитывая его плотность и массу . Используйте простое уравнение объема
V = m / d.Рассчитайте объем сжатого газа в баллоне, используя уравнение идеального газа.
Как найти объем * прямоугольника * по сравнению с объемом * коробки *
Вы не можете рассчитать объем прямоугольника , объем круга или объем квадрата, потому что это двухмерные геометрические фигуры.Таким образом, прямоугольник не имеет объема (но имеет площадь). Вероятно, вы ищете объем прямоугольного кубоида (или, говоря более общим языком, вы хотите найти объем коробки), который представляет собой трехмерный объект.
Чтобы найти объем коробки, просто умножьте длину, ширину и высоту — и готово! Например, если размер коробки 5х7х2 см, то объем коробки составляет 70 кубических сантиметров.
Для размеров, которые представляют собой относительно небольшие целые числа, легко вычислить объем вручную.Для больших или десятичных чисел использование калькулятора объема очень эффективно.
В реальной жизни есть много приложений, в которых может пригодиться калькулятор объема. Один из таких примеров — строительство дорог или тротуаров, где должны быть построены бетонные плиты. Как правило, бетонные плиты представляют собой твердые тела прямоугольной формы, поэтому можно использовать калькулятор бетона, который является приложением калькулятора объема.
Также формулы объема могут быть полезны, если вы увлеченный садовник или просто счастливый обладатель дома с двором.Ознакомьтесь с нашими замечательными инструментами, такими как:
Более того, вы можете встретить объем у себя на кухне или в ванной: у любой жидкости, которую мы пьем (например, воды в бутылках), а также косметических товаров или зубной пасты на упаковке продукта указан объем (в миллилитрах / литрах или жидких унциях). / галлоны).
Еще одно родственное приложение, хотя и немного другое, — это концепция площади поверхности. Предположим, что весь фасад здания должен быть окрашен. Чтобы знать, сколько нужно купить краски, необходимо рассчитать площадь здания.Удобный в использовании калькулятор площади рассчитает это за вас.
FAQ
Как найти объем?
Формула объема зависит от формы объекта . Одна из самых популярных форм — прямоугольная призма, также известная как коробка, где вы можете просто умножить длину на ширину на высоту , чтобы найти ее объем. Другой распространенной формой является цилиндр — чтобы найти его объем, умножьте высоту цилиндра на площадь его основания (π ⨉ r 2 ).Для других трехмерных фигур проверьте Калькулятор объема Omni.
Как измерить объем?
Измерение объема зависит от состояния вещества вашего объекта. Для жидкостей вы можете использовать мерный цилиндр или бюретку для измерений в химической лаборатории или мерный стакан и ложку для повседневных целей. Что касается газов, чтобы приблизительно измерить объем, вы можете надуть баллон и использовать его для вытеснения воды в мерном цилиндре. Аналогичный метод работает для твердых тел — поместите объект в градуированный контейнер и измерьте изменение показаний.
Объем — квадрат или куб?
Объем — это «куб» , так как это трехмерная мера. Площадь — это «квадратное» значение, поскольку площадь фигуры охватывает два измерения. Вы можете вспомнить, что объем представляет собой кубическое значение, вспомнив несколько названий единиц объема, например, кубических метров , кубических футов или кубических ярдов .
Как рассчитать объем?
В зависимости от формы объекта вы можете использовать разные формулы для расчета объема:
- Объем куба = сторона 3 .
- Кубоид (прямоугольная коробка) объем = длина ⨉ ширина ⨉ высота
- Объем сферы = (4/3) ⨉ π ⨉ радиус 3
- Объем цилиндра = π ⨉ радиус 2 ⨉ высота
- Объем конуса = (1/3) ⨉ π ⨉ радиус 2 ⨉ высота
- Объем пирамиды = (1/3) площадь основания ⨉ высота
В чем измеряется объем?
Кубический метр — единица объема в системе СИ.Однако, поскольку это непрактично, чаще всего вы можете встретить объем, выраженный в:
.
- Кубические сантиметры
- Кубические дюймы
- Миллилитры
- литров
- галлонов
Как найти объем жидкости?
Градуированные цилиндры и Колбы Эрленмейера подойдут, если вам нужно приблизительно измерить объем жидкости. Для более точных измерений нужно использовать мерную пипетку и бюретку.Однако, если вы печете торт или готовите вкусное блюдо и в рецепте используются единицы измерения объема, вы можете просто использовать мерный стакан, стакан или ложку.
Какая единица измерения объема в системе СИ?
Кубический метр (м 3 ) — единица измерения объема в системе СИ. Он образован от основной единицы длины в системе СИ — метра. Хотя кубический метр является основной единицей СИ, чаще используются другие единицы: для метрической системы популярны миллилитры, литры или кубические сантиметры, а для имперской системы вы можете найти объем, выраженный в пинтах, галлонах, кубических дюймах и т. Д. кубические футы или кубические ярды.
Объемный объем интенсивный или обширный?
Объем — это обширное свойство , такое же, как количество вещества, массы, энергии или энтропии. Обширное свойство — это мера, в которой зависит от количества вещества . Посмотрите на этот пример: стакан, бочка и бассейн, полный воды, имеют разные объем и массу ( расширенных свойств ), но вода в этих трех контейнерах будет иметь одинаковую плотность, показатель преломления и вязкость ( интенсивных свойств ). ).
В чем разница между площадью поверхности и объемом?
Объем — это трехмерная мера , а площадь поверхности — двумерная . Объем сообщает нам о кубическом пространстве, которое занимает объект, а площадь поверхности — это сумма всех областей, образующих трехмерную форму. Возьмем, например, картонную коробку 📦:
- Объем — это объем места, занимаемый коробкой, то есть свободного места внутри коробки
- Площадь поверхности — это пространство , занимаемое сторонами коробки , вычисленное при покраске сторон или упаковке коробки в бумагу.
Как найти объем объекта неправильной формы?
Вы можете использовать метод смещения жидкости для твердых объектов неправильной формы:
- Заполните емкость водой и отметьте уровень воды.
- Бросьте ваш объект внутрь и снова отметьте уровень. Убедитесь, что ваш объект не растворяется в воде.
- Для масштабируемых контейнеров вы можете всего вычесть исходного объема из нового объема. И все, поздравляю!
Но если на вашем оригинальном контейнере нет весов:
- Вынуть предмет.
- Заполните вашу емкость водой до второй отметки, залейте этой воды в мерный цилиндр / другую мерную емкость.
- Повторите шаг 6 для другого отмеченного уровня и вычтите объемы.
- Пат себе на спину — вы нашли объем объекта неправильной формы!
Что измеряет объем?
Объем измеряет пространства, занимаемого объектом в трех измерениях .Еще один близкий термин — вместимость, то есть объем внутреннего пространства объекта. Другими словами, вместимость описывает, сколько контейнер может вместить (воды, газа и т. Д.).
Каков объем Земли?
Объем Земли приблизительно равен 1,08321 × 10 12 км 3 ( 1,08 квадриллион кубических километров ), или 2,59876 × 10 11 кубических миль ( 259 триллионов кубических миль ). Вы можете получить этот результат, используя формулу объема сферы (4/3) ⨉ π ⨉ radius 3 и предполагая, что средний радиус Земли составляет 6371 километр (3958.76 миль).
Как рассчитать отношение площади поверхности к объему?
Чтобы вычислить отношение площади поверхности к объему SA: V, вы просто разделите площадь поверхности на объем . Для некоторых выбранных форм:
- Соотношение SA: V для куба = (сторона 6 ⨉ 2 ) / (сторона 3 ) = 6 / сторона
- Отношение SA: V для сферы = (4 ⨉ π ⨉ радиус 2 ) / ((4/3) ⨉ π ⨉ радиус 3 ) = 3 / радиус
- Соотношение SA: V для цилиндра = (2 ⨉ π ⨉ радиус 2 + 2 ⨉ π ⨉ радиус ⨉ высота) / (π ⨉ радиус 2 ⨉ высота) = 2 ⨉ (радиус + высота) / ( радиус ⨉ высота)
Расчетный объем | SkillsYouNeed
На этой странице объясняется, как рассчитать объем твердых объектов, т.е.е. насколько вы могли бы поместиться в предмет, если бы, например, вы залили его жидкостью.
Площадь — это мера того, сколько места находится внутри двухмерного объекта (подробнее см. Нашу страницу: Расчет площади).
Объем — это мера пространства внутри трехмерного объекта. Наша страница, посвященная трехмерным формам, объясняет основы таких форм.
В реальном мире вычисление объема, вероятно, не то, что вы будете использовать так часто, как вычисление площади.
Однако это все еще может быть важным. Возможность рассчитать объем позволит вам, например, определить, сколько у вас есть места для упаковки при переезде, сколько офисного пространства вам нужно или сколько варенья вы можете уместить в банку.
Это также может быть полезно для понимания того, что имеют в виду средства массовой информации, когда говорят о пропускной способности плотины или течении реки.
Примечание к единицам
Площадь выражается в квадратных единицах, потому что это два измерения, умноженные вместе.
Объем выражается в кубических единицах, потому что это сумма трех измерений (длина, ширина и глубина), умноженных вместе. Кубические единицы включают см 3 , м 3 и кубические футы.
ВНИМАНИЕ!
Объем также можно выразить как вместимость по жидкости.
Метрическая система
В метрической системе объем жидкости измеряется в литрах, что напрямую сопоставимо с кубическим размером, поскольку 1 мл = 1 см 3 .1 литр = 1000 мл = 1000 см 3 .
Британская / английская система
В британской / британской системе эквивалентными измерениями являются жидкие унции, пинты, кварты и галлоны, которые нелегко перевести в кубические футы. Поэтому лучше придерживаться жидких или твердых единиц объема.
Подробнее см. На нашей странице Системы измерения
Основные формулы для расчета объема
Объем прямоугольных тел
В то время как основная формула для площади прямоугольной формы — длина × ширина, основная формула для объема — длина × ширина × высота.
То, как вы относитесь к различным размерам, не меняет расчет: например, вы можете использовать «глубину» вместо «высоты». Важно то, что три измерения умножаются. Вы можете умножать в любом порядке, поскольку это не изменит ответ (подробнее см. Нашу страницу о умножении ).
Коробка размером 15 см в ширину, 25 см в длину и 5 см в высоту имеет объем:
15 × 25 × 5 = 1875 см 3
Объем призм и цилиндров
Эта базовая формула может быть расширена для охвата цилиндров и призм .Вместо прямоугольного конца у вас просто другая форма: круг для цилиндров, треугольник, шестиугольник или любой другой многоугольник для призмы.
Фактически, для цилиндров и призм объем — это площадь одной стороны, умноженная на глубину или высоту формы.
Таким образом, основная формула для определения объема призм и цилиндров:
Площадь формы торца × высота / глубина призмы / цилиндра.
Объем конусов и пирамид
Тот же принцип, что и выше (ширина × длина × высота), применяется для вычисления объема конуса или пирамиды, за исключением того, что, поскольку они достигают точки, объем составляет только долю от общего количества, которое было бы, если бы они продолжались. в той же форме насквозь.
Объем конуса или пирамиды составляет ровно одну треть от объема коробки или цилиндра с таким же основанием.
Таким образом, формула:
Площадь основания или торца × высота конуса / пирамиды × 1 / 3
Вернитесь на нашу страницу Расчет площади , если вы не можете вспомнить, как рассчитать площадь круга или треугольника.
Например, чтобы вычислить объем конуса с радиусом 5 см и высотой 10 см:
Площадь внутри круга = πr2 (где π (пи) приблизительно равно 3.14 и r — радиус окружности).
В этом примере площадь основания (круга) = πr 2 = 3,14
× 5 × 5 = 78,5 см 2 .78,5 × 10 = 785
785 × 1/3 = 261,6667 см 3
Объем сферы
Как и в случае с кругом, вам нужно π (пи) для вычисления объема сферы.
Формула: 4/3 × π × радиус 3 .
Вам может быть интересно, как определить радиус шара.Если не протыкать через него спицу (эффективный, но конечный для мяча!), Есть способ попроще.
Вы можете измерить расстояние вокруг самой широкой точки сферы напрямую, например, с помощью рулетки. Этот круг является окружностью и имеет тот же радиус, что и сама сфера.
Длина окружности вычисляется как радиус 2 x π x.
Чтобы вычислить радиус по окружности, вы:
Разделите окружность на (2 x π) .
Рабочие примеры: расчет объема
Пример 1
Вычислите объем цилиндра длиной 20 см, круговой конец которого имеет радиус 2,5 см.
Сначала обработайте площадь одного из круглых концов цилиндра.
Площадь круга равна πr 2 (π × радиус × радиус). π (пи) приблизительно равно 3,14.
Таким образом, площадь конца равна:
3.14 x 2,5 x 2,5 = 19,63 см 2
Объем — это площадь конца, умноженная на длину, и, следовательно, составляет:
19,63 см 2 x 20 см = 392,70 см 3
Пример 2
Что больше по объему: сфера радиусом 2 см или пирамида с основанием в квадрате 2,5 см и высотой 10 см?
Сначала определим объем сферы .
Объем сферы равен 4/3 × π × радиус 3 .
Таким образом, объем сферы составляет:
.
4 ÷ 3 x 3,14 × 2 × 2 × 2 = 33,51 см 3
Затем определите объем пирамиды .
Объем пирамиды 1/3 × площадь основания × высота.
Площадь основания = длина × ширина = 2,5 см × 2,5 см = 6,25 см 2
Объем, следовательно, равен 1/3 x 6,25 × 10 = 20.83см 3
Таким образом, сфера больше по объему, чем пирамида.
Расчет объема твердых частиц неправильной формы
Точно так же, как вы можете вычислить площадь неправильных двумерных форм, разбив их на правильные, вы можете сделать то же самое для вычисления объема неправильных твердых тел. Просто разделите твердое тело на более мелкие части, пока не получите только твердые тела, с которыми вы сможете легко работать.
Рабочий пример
Вычислите объем водяного цилиндра общей высотой 1 м, диаметром 40 см и полусферической верхней частью.
Сначала вы делите фигуру на две части: цилиндр и полусферу (полусферу).
Объем сферы равен 4/3 × π × радиус 3 . В этом примере радиус составляет 20 см (половина диаметра). Поскольку верхняя часть является полусферической, ее объем будет вдвое меньше полной сферы. Таким образом, объем данного участка формы:
.
0,5 × 4/3 × π × 203 = 16,755,16 см 3
Объем цилиндра равен площади основания × высоте.Здесь высота цилиндра — это общая высота за вычетом радиуса сферы, которая составляет 1 м — 20 см = 80 см. Площадь базы 2 грн.
Таким образом, объем цилиндрического сечения данной формы составляет:
80 × π × 20 × 20 = 100 530,96 см 3
Таким образом, общий объем этого резервуара для воды составляет:
100 530,96 + 16 755,16 = 117 286,12 см 3 .
Это довольно большое число, поэтому вы можете преобразовать его в 117.19 литров путем деления на 1000 (поскольку в литре 1000 см 3 ). Однако вполне правильно выразить его как cm 3 , поскольку задача не требует, чтобы ответ был выражен в какой-либо конкретной форме.
Дополнительная литература по навыкам, которые вам нужны
Понимание геометрии
Часть необходимых навыков Руководство по счету
Эта электронная книга охватывает основы геометрии и рассматривает свойства форм, линий и твердых тел.Эти концепции выстроены в книге с отработанными примерами и возможностями, позволяющими вам практиковать свои новые навыки.
Если вы хотите освежить в памяти основы или помочь детям в учебе, эта книга для вас.
В заключение…
Используя эти принципы, если необходимо, теперь вы сможете рассчитать объем практически всего в своей жизни, будь то упаковочный ящик, комната или водяной баллон.
Объемный анализ
Объемный анализ — широко используемый количественный аналитический метод.Как следует из названия, этот метод включает измерение объема раствора известной концентрации, который используется для определения концентрации аналита.
- Приготовьте раствор из точно взвешенного образца до +/- 0,0001 г анализируемого материала.
- Выберите вещество, которое будет быстро и полностью реагировать с аналитом, и приготовьте стандартный раствор этого вещества. Концентрация стандартного раствора должна составлять +/- 0.0001 М.
- Поместите стандартный раствор в бюретку и медленно добавьте его к неизвестному. Этот процесс называется титрованием, а раствор в бюретке — титрантом. Продолжайте титрование до завершения реакции; то есть до тех пор, пока количество добавляемого реагента не станет точно тем количеством, которое требуется для реакции со всеми анализируемыми составляющими. Эта точка называется точкой эквивалентности, и ее можно обнаружить, добавив индикатор к неизвестному раствору перед началом титрования.Индикатор — это вещество, которое дает изменение цвета в точке эквивалентности или около нее. Точка, в которой происходит изменение цвета, является конечной точкой титрования.
- Измерить необходимый объем стандартного раствора по показаниям бюретки до и после титрования. Поскольку молярность стандартного раствора известна, количество молей титранта можно рассчитать. Зная уравнение реакции, можно также рассчитать количество молей компонента, присутствующего в образце.
- Самый точный и удобный способ приготовления стандартного раствора — взвесить реагент, растворить его и разбавить раствор до определенного объема в мерной колбе. Этот метод можно использовать только в том случае, если реагент является первичным стандартом.
- Чтобы реагент был первичным стандартом, он должен быть доступным в чистом виде (как правило, с чистотой не менее 99,98%), стабильным как в чистом виде, так и в растворе, легко сушиться и оставаться сухим, а также растворимым в подходящем растворителе .
- Многие полезные реагенты не соответствуют этим требованиям, поэтому реагент растворяется и разбавляется приблизительно до желаемой концентрации. Затем раствор стандартизируют путем титрования его относительно первичного раствора. Этот стандартизованный раствор называется вторичным стандартом.
- Очистите бюретку перед использованием и промойте водой. Если на стенках скапливаются капли воды, бюретка не чистая. После очистки бюретки промойте ее титрантным раствором перед заполнением.Налейте около 5 мл титранта в бюретку и, удерживая бюретку почти горизонтально, медленно поверните ее так, чтобы титрант очистил бюретку целиком. Сделайте это трижды.
- Поместите бюретку в зажим для бюретки, прикрепленный к большой кольцевой стойке. С помощью воронки заполните бюретку титрантом до уровня выше нулевой отметки. Поместите стакан под бюретку и откройте кран на несколько секунд, чтобы удалить весь воздух из наконечника и заполнить его. Верх раствора теперь должен быть ниже нулевой отметки.
- Считайте показание бюретки до +/- 0,01 мл с мениском на уровне глаза, чтобы минимизировать параллакс (см. Рис. 1). Параллакс — это изменение видимого положения мениска на уровне глаз. Если вы смотрите на мениск, показания будут низкими. Если вы посмотрите на него, значение будет высоким.
Рис. 1. Поместите черную полосу за бюреткой, чтобы было легче увидеть мениск и облегчить чтение объема.
- Поместите титруемый раствор в колбу Эрленмейера и добавьте 3-5 капель соответствующего индикатора.Поместите колбу под бюретку.
- Медленно добавьте титрант из бюретки, взбалтывая содержимое колбы, чтобы обеспечить необходимое перемешивание (см. Рисунок 2). По мере приближения к конечной точке титрант нужно добавлять очень медленно — по капле за раз. Обычно есть индикация приближения к конечной точке. Если конечной точкой является изменение цвета, изменение происходит мгновенно, когда реагент падает в раствор, но исчезает при перемешивании в раствор. Это затухание происходит медленнее по мере приближения к конечной точке.
Рис. 2. Правильное обращение с запорным краном бюретки. Это позволяет максимально контролировать скорость добавления титранта.
- Когда будет достигнута конечная точка, дайте раствору отстояться в течение 10 секунд, чтобы жидкость в бюретке могла осесть, затем считайте показания бюретки. Вычтите начальное показание бюретки из окончательного, чтобы получить объем использованного титранта.
Индикаторы используются для определения конечной точки титрования.Индикатор используется при кислотно-основном и окислительно-восстановительном титровании. Изменение цвета индикатора должно быть около точки эквивалентности реакции. На следующих графиках показаны часто используемые индикаторы и их цвет.
Кислотно-основные показатели
Рис. 3. Раствор, содержащий индикаторный фенолфталеин, перед титрованием.
Рис. 4. Раствор, содержащий фенолфталеин, после титрования.
Индикаторы окисления-восстановления
Проверка по сравнению с ПЭТ у пациентов с зависимой от потока вазодилатации или без нее
Потенциальным ограничением нашей методики является то, что только высококачественные записи доплеровских спектров
требуют оптимального
позиционирования FloWire и правильного выбора затвора,
обеспечивают оптимальные результаты.Это ограничение, однако, еще больше касается
обычных измерений FloWire.
ЗАКЛЮЧЕНИЕ
Мы представляем, насколько нам известно, впервые
валидацию in vivo на людях процедуры внутри-
коронарного измерения Q с использованием доплеровской системы FloWire
, которая может учитывать изменения профиля потока и площади судна
. Эта способность имеет особое клиническое значение, потому что
изменений диаметра коронарных артерий происходят с зависимым от потока
вазодилатации.Этот метод обеспечивает точные данные по CFR как
, подтвержденным валидацией по сравнению с ПЭТ MPR, что представляет собой
как неинвазивный золотой стандарт.
ПОДТВЕРЖДЕНИЕ
Это исследование было частично профинансировано за счет грантов Швейцарского национального научного фонда
(грант SNSF-профессора
PP00A-68835 и грант 3100-068368).
СПРАВОЧНАЯ ИНФОРМАЦИЯ
1. Кампизи Р., Чернин Дж., Шредер Х., Сайре Дж. В., Шельберт Х.Р. L-аргинин нормальный-
определяет коронарную вазомоторную реакцию у курильщиков, длительно куривших.Тираж. 1999; 99: 491– 497.
2. Кауфманн П.А., Некки-Русконе Т., ди Терлицци М., Шаферс К.П., Люшер Т.Ф.,
Камичи П.Г. Ишемическая болезнь сердца у курильщиков: витамин С восстанавливает коронарную
микроциркуляторную функцию. Тираж. 2000; 102: 1233–1238.
3. Гетлин М., Касел А.М., Коппенрат К., Циглер С., Делиус В., Швайгер М.
Отсроченный ответ резерва миокардиального кровотока на гиполипидемическую терапию
flувастатином. Тираж. 1999; 99: 475–481.
4. Кауфманн П.А., Некки-Русконе Т., Шаферс К.П., Люшер Т.Ф., Камичи П.Г. Низкий уровень холестерина липопротеидов
плотности и коронарная микрососудистая дисфункция при гипер-
холестеринемии. J Am Coll Cardiol. 2000; 36: 103–109.
5. Оферк Д., Молл Дж., Зебе Х. и др. Снижение коронарного резерва: механизм
стенокардии у пациентов с артериальной гипертензией и нормальной коронарной артерией —
гг. Тираж. 1984; 69: 1–7.
6. Ди Карли М.Ф., Бьянко-Батлес Д., Ланда М.Э. и др.Влияние вегетативной нервной системы на коронарный кровоток у пациентов с сахарным диабетом. Тираж.
1999; 100: 813–819.
7. Кауфманн П.А., Камичи П.Г. Измерение кровотока в миокарде с помощью ПЭТ: технические аспекты и клинические применения. J Nucl Med. 2005; 46: 75–88.
8. Де Брюйн Б., Пейлс Н.Х., Смит Л., Вивегг М., Хейндриккс Г.Р. Коронарный
термодилюция для оценки резерва потока: экспериментальная проверка. Тираж. 2001;
104: 2003–2006.
9. Николс В.В., О’Рурк MF. Природа течения жидкости. В: Nichols WW,
O’Rourke MF, eds. Макдональдс Кровоток в артериях. 3-е изд. Лондон, Великобритания:
Эдвард Арнольд; 1990: 12–53.
10. Дженни Р., Кауфманн П.А., Цзян З., Аттенхофер С., Линка А., Мандинов Л. In vitro
Подтверждение измерения объемного кровотока с помощью доплеровской проволоки.
Ультразвук Med Biol. 2000; 26: 1301–1310.
11. Дженни Р., Мэтьюз Ф., Ашкенаси С.В. и др.Новая процедура in vivo для измерения объемного расхода
. Ультразвук Med Biol. 2004; 30: 633–637.
12. Мандинов Л., Кауфманн П., Штауб Д., Бэкингем Т.А., Аманн Ф.В., Гесс О.М.
Коронарная вазомоция после чрескожной транслюминальной коронарной ангиопластики de-
зависит от тяжести основного поражения. J Am Coll Cardiol. 1997; 30: 682–688.
13. Cerqueira MD, Verani MS, Schwaiger M, Heo J, Iskandrian AS. Профиль безопасности аденозиновой стресс-перфузионной визуализации
: результаты реестра многоцентрового исследования Аденоскан
.J Am Coll Cardiol. 1994; 23: 384–389.
14. Кауфманн П.А., Некки-Русконе Т., Яп Дж. Т., Римольди О., Камичи П. Г.. Оценка
воспроизводимости исходных и гиперемированных измерений кровотока в миокарде —
измерений с водой, меченной 15O, и ПЭТ. J Nucl Med. 1999; 40: 1848–1856.
15. Wyss CA, Koep i P, Mikolajczyk K, Burger C, von Schulthess GK, Kaufmann
PA. Велосипедная физическая нагрузка в ПЭТ для оценки резерва коронарного кровотока:
Воспроизводимость и сравнение с аденозиновым стрессом.J Nucl Med. 2003; 44: 146 —
154.
16. Challis RE, Kitney RI. Обработка биомедицинских сигналов (в четырех частях). Часть 2. Частотные преобразования
и их взаимосвязи. Med Biol Eng Comput. 1991;
29: 1–17.
17. Кауфманн П., Вассалли Г., Утцингер У., Гесс ОМ. Коронарная вазомоция во время динамических упражнений
: влияние никардипина внутривенно и внутрикоронарно. JAm
Coll Cardiol. 1995; 26: 624 — 631.
18. Кауфманн П., Мандинов Л., Гесс О.М.Сужение сосудов коронарного стеноза: влияние
на ишемию миокарда. Eur Heart J. 1997; 18: 1853–1859.
19. Кауфманн П.А., Фрилингсдорф Дж., Мандинов Л., Зайлер С., Хуг Р., Хесс О.М. Устранение
аномальной коронарной вазомоции антагонистами кальция у пациентов с гипер-
холестеринемией. Тираж. 1998; 97: 1348–1354.
20. Хермансен Ф., Эшбернер Дж., Спинкс Т.Дж., Кунер Дж.С., Камичи П.Г. Создание изображений миокардиального фактора
непосредственно из динамического сканирования h315O без использования сканирования пула крови
C15O.J Nucl Med. 1998; 39: 1696–1702.
21. Кауфманн П.А., Ширло С., Павличек В. и др. Повышенный кровоток в миокарде
во время острого воздействия на смоделированных высотах. J Nucl Cardiol. 2001; 8: 158–164.
22. Wyss CA, Koep i P, Fretz G, Seebauer M, Schirlo C, Kaufmann PA. Влияние
высотной экспозиции на резерв коронарного потока. Тираж. 2003. 108: 1202–1207.
23. Koep i P, Hany TF, Wyss CA, et al. Коррекция затухания КТ для количественной оценки перфузии миокарда
с использованием гибридного сканера ПЭТ / КТ.J Nucl Med. 2004; 45:
537–542.
24. Wyss CA, Koep i P, Namdar M, et al. Тетрагидробиоптерин восстанавливает нарушенную
коронарную микрососудистую дисфункцию при гиперхолестеринемии. Eur J Nucl Med
Mol Imaging. 2005; 32: 84–91.
25. Cerqueira MD, Weissman NJ, Dilsizian V, et al. Стандартизированный сегмент миокарда
и номенклатура для томографической визуализации сердца: заявление
для медицинских работников от Комитета кардиологической визуализации Совета
по клинической кардиологии Американской кардиологической ассоциации.Тираж. 2002;
105: 539 –542.
26. Бланд Дж. М., Альтман Д. Г.. Статистические методы для оценки соответствия между двумя методами клинического измерения
. Ланцет. 1986; 8: 307–310.
27. Джагатесан Р., Кауфманн П.А., Розен С.Д. и др. Оценка долгосрочной воспроизводимости
исходного уровня и добутамин-индуцированного миокардиального кровотока у
пациентов со стабильной ИБС. J Nucl Med. 2005; 46: 212–219.
28. Кауфманн П.А., Дженни Р.К оценке резерва коронарного потока только по профилям средней скорости
следует относиться с осторожностью. J Am Coll Cardiol. 2000;
35: 1363–1365.
29. White CW, Wright CB, Doty DB и др. Предсказывает ли визуальная интерпретация коронарной артериограммы
физиологическое значение коронарного стеноза? N Engl
J Med. 1984; 310: 819–824.
30. Zijlstra F, van Ommeren J, Reiber JH, Serruys PW. Предсказывает ли количественная оценка
размеров коронарной артерии физиологическое значение
коронарного стеноза? Тираж.1987; 75: 1154–1161.
31. Тополь EJ, Nissen SE. Наша озабоченность коронарной люминологией: диссоциация между клиническими и ангиографическими данными при ишемической болезни сердца.
Тираж. 1995; 92: 2333–2342.
32. Гулд К.Л., Липскомб К., Гамильтон Г.В. Физиологические основы оценки критического стеноза коронарных артерий
. Am J Cardiol. 1974; 33: 87–92.
33. Гулд К.Л., Киркиид Р.Л., Бучи М. Резерв коронарного кровотока как физиологический
мера степени тяжести стеноза.J Am Coll Cardiol. 1990; 15: 459–474.
34. Бах Р.Г., Донохью Т.Дж., Керн М.Дж. Измерение скорости интракоронарного допплеровского кровотока —
единиц для оценки и лечения ишемической болезни сердца. Curr Opin
Cardiol. 1995; 10: 434–442.
35. Судхир К., Харгрейв В.К., Джонсон Э.Л. и др. Измерение объемного коронарного кровотока
с помощью допплеровского катетера: проверка на модели на животных. Am Heart J.
1992; 124: 870-875.
36. Doucette JW, Corl PD, Payne HM, et al.Проверка доплеровского проводника для внутрисосудистого измерения скорости кровотока в коронарной артерии
. Тираж. 1992;
85: 1899 –1911.
37. Лабовиц А.Дж., Антонис Д.М., Кравенс Т.Л., Керн М.Дж. Проверка измерений объемного потока
с помощью проводника для коронарной ангиопластики с доплеровским наконечником.
Am Heart J. 1993; 126: 1456–1461.
38. Набель Э.Г., Селвин А.П., Ганц П. Крупные коронарные артерии у людей
реагируют на изменение кровотока: эндотелий-зависимый механизм, который не работает у
пациентов с атеросклерозом.J Am Coll Cardiol. 1990; 16: 349–356.
39. Россен Дж. Д., Квиллен Дж. Э., Лопес А. Г., Стенберг Р. Г., Талман К. Л., Виннифорд М. Д..
Сравнение коронарной вазодилатации при внутривенном введении дипиридамола и адено-
синуса. J Am Coll Cardiol. 1991; 18: 485–491.
40. Россен Дж. Д., Оскарссон Х., Минор Р. Л. и др. Влияние антагонизма аденозина на
метаболически опосредованную коронарную вазодилатацию у людей. J Am Coll Cardiol.
1994; 23: 1421–1426.
41. Jenni R, Buchi M, Zweifel HJ, Ritter M.Влияние размера доплеровского проводника и скорости потока
на профили внутрисосудистой скорости. Катет Кардиоваск Диагностика. 1998; 45:
96–100.
ЗАПАС ОБЪЕМНОГО КОРОНАРНОГО ПОТОКА • Kaufmann et al. 1277
от 6 мая 2015 г. Только для личного пользования. jnm.snmjournals.org Скачано с
Примеры объемных пленок
Если вы хотите посмотреть объемные фильмы, чтобы ощутить творческий потенциал, ознакомьтесь с проектами ниже. Для некоторых требуются специализированные гарнитуры виртуальной реальности или дополненной реальности, другие доступны в Интернете или на мобильных устройствах.
по Scatter
Основанный на полнометражном документальном фильме «Нулевые дни», снятом Алексом Гибни, «Zero Days VR», созданный на основе полнометражного документального фильма «Нулевые дни», предлагает новое измерение оригинальной функции, рассказывая историю с точки зрения, которая была невозможна до появления виртуальной реальности. Опыт Zero Days VR визуализирует историю Stuxnet по-новому: зрители будут помещены в невидимый мир компьютерных вирусов, которым предстоит столкнуться с высокими ставками кибервойны в человеческом масштабе.Zero Days VR — это первый объемный опыт, получивший премию «Эмми»!
Испытайте Zero Days VR на Oculus Rift, Oculus Go, Steam VR
Джонатан Минард и Джеймс Джордж (соучредитель, Scatter)
В Интернете появилось поколение художников и хакеров, использующих технологии с открытым исходным кодом для экспериментов в искусстве и дизайне. ОБЛАКА — это интерактивный документальный фильм и портрет этого сообщества пионеров цифровых технологий, исследуемый через призму кода.Проект задает вопросы о будущем творчества в то время, когда алгоритмы играют важную роль в формировании культуры.
CLOUDS стал родоначальником Depthkit, первого интерактивного документального фильма, в котором использовалась комбинация объемного видеозахвата с виртуальной реальностью.
Испытайте CLOUDS на Oculus Rift или Desktop (ПК / Mac)
от TheWaveVR
Награжденный премией Грэмми исполнитель звукозаписи и новатор в музыкальных технологиях Имоджен Хип и TheWaveVR, революционная платформа социальной виртуальной реальности (VR), объединились для создания первого в своем роде иммерсивного музыкального представления.
Imogen Heap VR основан на голографическом опыте с Depthkit, где Имоджин исполняет серию песен, включая неизданный трек Фру Фру и совершенно новый микс «Hide and Seek». Спектакль, дебютировавший на TheWaveVR, переносит зрителей в домашнюю студию Имоджин в Лондоне.
Смотрите концерт Имоджен Хип TheWaveVR на Oculus Rift или Steam
Universe Within: Digital Lives in the Global Highrise — это интерактивный документальный фильм, который переносит нас в квартиры, сердца, умы и компьютеры вертикальных граждан по всему миру, чтобы раскрыть цифровое состояние человека в 21 веке.Можем ли мы найти в сети любовь, ненависть, мир, бога, сообщество или лучший мир, пойманные в ловушку наших высотных подразделений?
Познакомьтесь с вселенной Highrise в в Интернете
от Google Data Arts
Virtual Art Sessions — это эксперимент Chrome в области искусства виртуальной реальности, созданный с помощью захватывающей программы для рисования Tilt Brush. Google объединился с шестью всемирно известными художниками, предложив им новый способ рисовать, рисовать и лепить. Их сеансы были записаны с помощью Depthkit и доступны в Интернете, так что вы можете изучить, как художники создавали свои творения виртуальной реальности под любым углом.
Участвующие художники: Андреа Бласич, Кристоф Ниманн, Харальд Белкер, Кэти Роджерс, Сын Юл О и Йок и Шерио
Посетите сеансы виртуального искусства в Интернете
Загляните за кулисы с Джеффом Нусом и его командой.
Ширин Анлен и Ор Флейшер
В начале 2017 года площадь Цина Дизенгоф, одно из знаковых мест Тель-Авива, была снесена. Площадь была домом для одиноких и маргинальных персонажей этого района.Этот проект рассказывает о людях, которые тяготели к площади и проводили на ней свои дни. В этом интерактивном документальном фильме о WebVR они рассказывают о своей жизни и мире. Цина: симфония тоски приглашает зрителя на физическую прогулку, чтобы исследовать площадь и ее персонажей в разное время дня, с элементами анимации, фэнтези и интерактивным звуком.
Посмотрите в Интернете «Симфонию страсти Тзина»
Поскольку это такой новый носитель, многие из недавних объемных фильмов все еще проходят фестивали в качестве инсталляций и еще не распространены.Хотя вы еще не можете загрузить их самостоятельно, прочтите ниже, чтобы узнать о предстоящих удивительных событиях.
по Scatter
Blackout — это документальный фильм о виртуальной реальности, в котором жители Нью-Йорка рассказывают свои истории собственным голосом. Blackout — это живой документ, продолжающийся совместный проект, в котором собираются истории реальных людей, живущих в этом городе в условиях сегодняшнего обострения политического климата. Blackout стремится преодолеть социальные различия, освещая моменты, когда наши жизни пересекаются в пространстве, где эти расслоения наиболее заметны — в метро Нью-Йорка.
Blackout демонстрирует готовящийся к выпуску продукт Depthkit Studio для многокамерной съемки всего тела на 360 градусов.
Послушайте интервью Scatter на Engadget и New Yorker Radio Hour.
, Центр общественного правосудия Браунсвилля, Народная культура
География Браунсвилля, Бруклин, разделена продолжающимся соперничеством между жилищными фондами. В этом документальном фильме о виртуальной реальности игроки с обеих сторон конфликта работают вместе, чтобы исследовать истории, истории и мечты сообщества и его жителей.Участвуя в этом симуляторе приключений в мире, игроки должны исследовать структурные реалии района, пытаясь ответить на простой вопрос; у нас больше общего, чем мы когда-то думали?
Прочтите о проекте на Engadget или послушайте интервью с командой на WNYC
Кадр из светлячков Браунсвилля
Автор: Аарон Брэдбери, NSC Creative
В этом творческом научно-популярном опыте используется мульти-повествовательный и объемный захват, чтобы путешествовать через разум Лизы, когда она вспоминает свою потерянную любовь, Эрика.Фрагменты воспоминаний об их совместной жизни появляются внутри пустоты и со временем запутываются в навязчивом видении, кульминацией которого является шокирующий момент смерти Эрика.
Vestige использует преимущества нового Zero Days Look, доступного в подключаемом модуле Unity v0.2.4.
Прочтите о создании фильма «Вести без кино»
Асад Дж. Малик, 1RIC
Терминал 3 — это интерактивный документальный фильм с дополненной реальностью, в котором исследуются современные мусульманские идентичности в США.С. через объектив допроса в аэропорту. Когда зрители надевают гололены, они вступают в сверхъестественное, чтобы напрямую допросить и определить судьбу пассажира голограммы перед ними. Эти допросы становятся поразительно личными встречами, которые заканчиваются только тогда, когда участник решает, впустить голограмму в страну или нет, — но здесь есть поворот.
Послушайте интервью с директором Терминала 3 Асадом Дж. Маликом на BBC или прочтите об этом на Fast Company
Илья Шилак и Кирилл Цибулски
Queerskins исследует динамическое напряжение между «реальным» и виртуальным, фактом и вымыслом, воспоминаниями и желаниями в убедительном повествовании, управляемом персонажами.История вращается вокруг сложных отношений между набожной католичкой матерью и ее сыном-геем, который умирает от СПИДа. Queerskins исследует типичное человеческое желание превзойти обычную реальность через память, веру и воображение.
Читайте о Queerskins в Forbes
Ирем Харнак, Элли Райнаи
Состоящий из фотографий и передовых объемных отзывов о виртуальной реальности, Made This Way: Redefining Masculinity — это интерактивный документальный фильм с использованием смешанных средств массовой информации, в котором исследуется, как трансгендерные мужчины бросают вызов гендерным нормам и пересматривают традиционные представления о мужественности.
Линетт Уоллворт
От легендарного художника / режиссера Линетт Уоллворт и амазонского народа Яванава, «Ававена» — это потрясающая история о метаморфозах, вторая из серии работ Линетт Уоллворт и продюсера Николь Ньюнхэм в смешанной реальности после их VR-фильма, получившего Эмми. «Столкновения».
Для амазонского Яванавы «медицина» имеет силу перенести вас в видении в место, где вы никогда не были. Хушуху, первая женщина-шаман Яванавы, использует виртуальную реальность как лекарство, чтобы открыть портал к другому способу познания.AWAVENA — это сотрудничество между сообществом и художником, объединяющее технологии и трансцендентный опыт, чтобы можно было поделиться видением и историей, рассказанной о людях, восставших на грани исчезновения.
Depthkit используется для съемки первой шаманки в качестве руководства, чтобы поделиться историей и видениями Яванавы. В этой захватывающей работе представлены флуоресцентные и биолюминесцентные образцы в ранее невидимых цветах из лесного мира, чтобы создать яркое, яркое видение.
Послушайте, как режиссер Линетт Уоллворт обсуждает свой процесс с BBC в студии
Кадр из Ававены
Габо Арора, Superbright и Sensorium
Понимание суфизма по самой своей природе основано на опыте.Это часто неправильно понимаемая ветвь ислама, которую часто называют эзотерической, мистической и далеко за пределами общепринятых практик. Но во многих мусульманских странах суфизм глубоко привязан к национальному наследию и другим художественным направлениям. Зикр позволяет четырем людям одновременно испытать суфизм так же, как практикующие в Тунисе, и вместе участвовать в ритуалах экстатической музыки и открывать новые духовные возможности.
Depthkit используется для захвата исполнения суфийских ритуалов, смешанных с 360-градусным видео для получения волшебного реального опыта.
Кадр из Зикра
От UNLTD
Trinity — это пилотный эпизод серии VR, действие которой происходит в будущем, в котором люди уже давно вымерли, а андроиды ведут последнюю войну против всемогущего ИИ.
Прочтите о Trinity в блоге Made with Unity
В Scatter мы считаем всех, кто использует Depthkit, своими творческими сотрудниками, помогающими формировать среду. У нас есть специальная программа Powered by Depthkit, предназначенная для оказания творческой, технической и производственной поддержки проектам нашего сообщества.

 Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.
Эти фигуры, исходя из названия класса, имеют прямые ребра и плоские грани. Грань — это плоскость, которая ограничивает фигуру. Место соединения двух граней называется ребром, а точка соединения трех граней — это вершина. К полиэдрам относятся геометрическая фигура куб, тетраэдры, призмы, пирамиды. Для этих фигур справедлива теорема Эйлера, которая устанавливает связь между числом сторон (С), ребер (Р) и вершин (В) для каждого полиэдра. Математически эта теорема записывается так: С + В = Р + 2.