Объемная геометрическая фигура из бумаги: Как сделать объемные геометрические фигуры из бумаги (схемы, шаблоны)?

by alexxlab Posted in Разное on 16.04.202114.03.2021

Содержание

Объемная игрушка из бумаги

А вот для вас загадки. Давайте разгадаем их.

1)
И в лесу, заметьте, дети,

Есть ночные сторожа.

Сторожей боятся этих

Мыши, прячутся, дрожа!

Очень уж суровы

Филины и … (Cовы)

2) Спереди – шильце, сзади – вильце,

Сверху – черное суконце,

Снизу – белое полотенце. (Ласточка)

3) Чернокрылый,

Красногрудый

И зимой найдет приют:

Не боится он простуды –

С первым снегом

Тут как тут! (Снегирь)

4)Зимой на ветках яблоки!

Скорей их собери!

И вдруг вспорхнули яблоки,

Ведь это … (снегири)

5) Черный жилет, красный берет.

Нос, как топор, хвост, как упор. (Дятел)

6) Гнездо свое он в поле вьет,

Где тянутся растения.

Его и песни и полет

Вошли в стихотворения!

Хочет – прямо полетит,

Хочет – в воздухе висит,

Камнем падает с высот

И в полях поет, поет. (Жаворонок)

7) Весь день рыбак в воде стоял,

Мешок рыбешкой набивал.

Закончив лов, забрал улов,

Поднялся ввысь – и был таков. (Пеликан)

8) Гнездо под крышей ловко строит,

Птенцов своих постоянно выводит,

Перед дождем очень низко летает,

Эту птичку каждый ребенок знает,

За ней мы любим наблюдать,

Эту птичку … (ласточкой) звать.

9) Вдоль по речке, по водице

Плывет лодок вереница,

Впереди корабль идет,

За собою их ведет,

Весел нет у малых лодок,

А кораблик больно ходок.

Вправо, влево, взад, вперед

Всю ватагу повернет. (Утка с утятами)

10) Хоть я не молоток –

По дереву стучу:

В нем каждый уголок

Обследовать хочу.

Хожу я в шапке красной

И акробат прекрасный. (Дятел)

Как сделать фигуру из бумаги схема. Тема: «Объемные геометрические фигуры

КОНСПЕКТ И МЕТОДИЧЕСКОЕ ОБЕСПЕЧЕНИЕ УРОКА (ЗАНЯТИЯ) ПО БУМАГОПЛАСТИКЕ.

Тема:
«Объемные геометрические фигуры».

Цели и задачи урока:
Развить у ученика образное объемно-пространственное мышление и воображение. Выполнение задания предполагает ознакомление с материалом, приобретение умения выполнять точный чертеж, вырезать разнообразные формы, умение пользоваться острыми режущими предметами (резак, ножницы), склеивать между собой детали и собирать объемную геометрическую фигуру.

Оборудование:
У преподавателя
: компьютер и проектор, образцы изделий, инструменты (ножницы, резак, бумага, линейка, карандаш, ластик, клей), шаблоны, инструкция по технике безопасности при работе с режущими инструментами, презентация. У учащихся
:
подкладная деревянная доска (30*20 см), ножницы, резак, бумага (ватман) А3 формата – 2 листа, линейка, карандаш (твердый), ластик, клей (момент «кристалл»).

Тип урока:
смешанный

Ход урока:

1. Организационный момент

–1 минуту.

Проверка готовности к уроку.

2. Объяснение учителя

– 9 минут.

Сообщение темы урока, цели и задачи.

Объяснение материала:

В процессе занятий преподаватель последовательно рассказывает и наглядно показывает о построении чертежей для объемных геометрических фигур и целенаправленно формирует у учащихся способность работать руками, приучает к точным движениям пальцев, совершенствует мелкую моторику рук, развивает глазомер.

— «Из листа бумаги с помощью резака, ножниц и клея можно быстро выполнить модель какого-либо изделия, несложную композицию, макет. В отличии от скульптуры из глины, где масса набирается методом наращивания и уточнения форм, в изделиях из бумаги отсутствует каркас. Почти все изделия – пустотелы и представляют собой как бы скорлупу. Однако это не оттиск с готовой формы, а совершенно самостоятельная пластическая оболочка, созданная за счет сгибов бумаги по предварительно нанесенным линиям – надрезам. Надрезы являются конструктивной основой всех изделий, выполняемых из бумаг (они называются – ребра жесткости). Согнутый пополам лист образует ребро. Если лист сложить несколько раз, то от количества и характера этих прямолинейных сгибов можно получить различную фактуру
».

Опорные качества способностей, формируемых занятиями, с одной стороны, относятся преимущественно к области восприятия (развитость аналитико-синтетического взгляда на предмет), с другой стороны – к области моторики (опциальная область руки). Основной формой проведения занятий является урок смешанного типа (лекция совмещается с практической работой).

3. Практическая работа учеников

– 1 час 20 минут.

Для работы выбраны макеты геометрических фигур различные по размеру и форме.

Ход работы:

1. На листе белой бумаги (ватман) намечаем размеры и контуры для создания геометрических фигур как указанно на шаблоне.

2. Вырезаем по контуру, делаем надрезы на внутренних ребрах фигуры с лицевой стороны. Убираем ластиком вспомогательные линии и сгибаем.

3. Смазываем клеем участки, обозначенные надписью «для клея» (как указанно на шаблоне) и приступаем к конструированию.

По такому же принципу выполняется задание со следующими геометрическими фигурами.

За 5 минут до окончания урока мини-просмотр и обсуждение работ.

Наглядный материал к уроку.

Призентация для урока
: Бумагопластика. Объемные геометрические фигуры.

Геометрическая пирамида.

http://pandia.ru/text/80/128/images/image005_30.jpg»>

Пояснение к слайду: 2. После нанесения чертежа, вырезаем по контуру (сплошная линия) и делаем надрезы резаком по линии обозначенной пунктиром. Вспомогательные линии удаляем ластиком

Октаэдр.

DIV_ADBLOCK219″>

3.Дополнительные вставки на фигуре обозначенные штриховкой смазываем клеем и склеиваем фигуру дополнительными вставками во внутрь.

додекаэдр.

http://pandia.ru/text/80/128/images/image009_14.jpg»>.

Пояснение к слайду: 2.После нанесения чертежа, вырезаем по контуру (сплошная линия) и делаем надрезы резаком по линии обозначенной пунктиром. Вспомогательные линии удаляем ластиком.

ИКОСАЭДР.

Пояснение к слайду: 1.Чертеж икосаэдра переносится на лист учащегося с точностью 1:1, как указанно на шаблоне. Построение начинается с равнобедренного треугольника одна сторона которого равна 4,5 см, а высота 4 см. Далее, как указанно на шаблоне, переносим чертеж всех оставшихся равнобедренных треугольников.

Пояснение к слайду: 2.После нанесения чертежа, вырезаем по контуру (сплошная линия) и делаем надрезы резаком по линии обозначенной пунктиром. Вспомогательные линии удаляем ластиком.

педагогический рисунок учителя.

примеры работ учащихся.

Объемные геометрические фигуры старшей группы 2/4 класса.

Преподаватель: .

Упражнение «Звезда»

Цели урока	Методы и приемы
· Дать представление об истории бумагопластики. · Познакомить с основными способами работы с бумагой в технике бумагопластика · Познакомить с основными этапами выполнения работы , научить аккуратности в ходе выполнения работы · Развить у ученика образное объемно-пространственное мышление и воображение. · Закрепить у обучающихся представление о бумагопластике.	Использование наглядности Самостоятельное выполнение Сравнение
Оборудование	Материалы
Мультимедиа Наглядное пособие	Чертежная бумага, канцелярский резак, ножницы, линейка, циркуль, карандаш, ластик	Выполнение упражнения «Звезда» в технике бумагопластика.
План урока	Образец работы
1.Организация 3 мин. 2.Вводная беседа 10 мин. 3.Самостоятельная работа 30 мин. 4.Заключение 2 мин.

1.Организационная часть.

Нашим заданием на сегодняшний урок будет упражнение в технике бумагопластики «звезда».

2.Объяснение материала.

Бумагопластика.

Что же это такое: скульптура из бумаги, архитектура или дизайн? Данный вид художественной деятельности в равной степени модно отнести ко всем названным направлениям, так как бумага, как проектный материал широко используют и художники, и архитекторы, и дизайнеры. Из листа бумаги с помощью резака, ножниц и клея можно быстро выполнить модель какого-либо изделия, несложную композицию, макет.

Бумажная пластика близка к скульптуре.

В отличие от скульптуры из глины, где масса набирается методом наращивания и уточнения форм, в изделиях из бумаги отсутствует каркас. Почти все изделия – пустотелы и представляют собой как бы скорлупу. Однако это не оттиск с готовой формы, а совершенно самостоятельная пластическая оболочка, созданная за счет сгибов бумаги по предварительно нанесенным линиям – надрезам.

Особенности технологии.

Надрезы являются конструктивной основой всех изделий, выполняемых из бумаг (далее они будут называться – ребра жесткости). Согнутый пополам лист образует ребро. Если лист сложить несколько раз, то от количества и характера этих прямолинейных сгибов можно получить различную фактуру. В Японии этот метод в бумаготворчестве называется — оригами.

Материалы и инструменты.

Главным инструментом в бумагопластике является резак (канцелярский нож). Ножницы нужны для разрезания бумаги, выполнения различных выкроек, надрезов, просечек и т. д. Линейка, желательно металлическая длиной 25-30 см, т. к. пластмассовые и деревянные линейки не точны, и быстро выходят из строя. Циркуль, для построения окружности и деления ее на шесть частей.

3.Выполение работы.

Сегодня мы познакомились с техникой бумагопластики, просмотрели мультимедийную презентацию по данному направлению, и на наглядном пособии просмотрели и потрогали что представляет из себя данная техника. А сейчас мы попробуем выполнить упражнение «звезда». Для этого на вашем рабочем месте должны лежать такие инструменты, как: линейка, карандаш, ластик, резак, ножницы. Упражнение будет выполняться из бумаги. У каждого из Вас так же на столах имеется шаблон по выполнению работы с заданными размерами. Обратите внимание: желтая линия – построение, по коричневой линии-вырезаем, прямые зеленые линии – надрезаем резаком и отгибаем от себя, зеленые линии-пунктир – надрезаем резаком и отгибаем на себя. Работу начинаем вести с отчерченного круга диаметром в 20 см. После чего приступаем к расчерчиванию вспомогательных линий и приступаем к конструированию.

4.Закрепление пройденного материала.

Вот и подошел к концу наш творческий урок. Мы с вами познакомились с новым направлением в искусстве — техникой бумагопластики. Так скажите мне пожалуйста, чем же отличается бумажная скульптура от скульптуры из глины? В какой стране за рубежом используется эта техника, и какого ее название там? Какие материалы могут нам понадобиться при создании бумажной композиции?

Большой выбор развёрток простых геометрических фигур.

Первое знакомство детей с бумажным моделированием всегда начинается с простых геометрических фигур, таких как кубик и пирамида. Не у многих получается склеить кубик с первого раза, иногда требуется несколько дней, чтобы сделать поистине ровный и безупречный куб. Более сложные фигуры цилиндр и конус требуют в несколько раз больше усилий нежели простой кубик. Если вы не умеете аккуратно клеить геометрические фигуры, значит и за сложные модели вам ещё рано браться. Займитесь сами и научите своих детей клеть эти «азы» моделирования по готовым развёрткам.

Для начала я, конечно же, предлагаю научиться клеить обычный кубик. Развёртки сделаны для двух кубиков, большого и маленького. Более сложной фигурой является маленький кубик потому, как клеить его сложнее, чем большой.

Итак, начнём! Скачайте развёртки всех фигур на пяти листах и распечатайте на плотной бумаге. Перед тем, как печатать и клеить геометрические фигуры обязательноознакомьтесь со статьёй о том, как выбрать бумагу и как вообще правильно вырезать, сгибать и клеить бумагу.

Для более качественной печати советую использовать программу AutoCAD, и даю вамразвёртки для этой программы , а также читайте, как распечатывать из автокада . Вырежьте развёртки кубиков с первого листа, по линиям сгиба обязательно проведите иголкой циркуля под железную линейку, чтобы бумага хорошо сгибалась. Теперь можно начинать клеить кубики.

Для экономии бумаги и на всякий пожарный я сделал несколько развёрток маленького кубика, мало ли вам захочется склеить не один кубик или что-то не получится с первого раза. Ещё одна несложная фигура это пирамида, её развёртки найдёте на втором листе. Подобные пирамиды стоили древние египтяне, правда не из бумаги и не таких маленьких размеров:)

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

Вот мы и добрались до сложных фигур. Теперь придётся поднапрячься, склеить такие фигуры нелегко! Для начала обычный цилиндр, его развёртки на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Чтобы аккуратно собрать цилиндр его детали нужно клеить встык. С одной стороны дно можно приклеить без проблем, просто поставьте на стол заранее склеенную трубку, положите на дно кружок и залейте клеем изнутри. Следите, чтобы диаметр трубы и круглого дна плотно подходили друг к другу, без щелей, иначе клей протечёт и всё приклеится к столу. Второй кружок приклеить будет сложнее, поэтому приклейте внутри вспомогательные прямоугольники на расстоянии толщины бумаги от края трубы. Эти прямоугольники не дадут упасть основанию внутрь, теперь вы без проблем приклеете кружок сверху.

Цилиндр с овальным основанием можно клеить также как и обычный цилиндр, но он имеет меньшую высоту, поэтому тут проще вставить внутрь гармошку из бумаги, а наверх положить второе основание и по краю приклеить клеем.

Теперь очень сложная фигура — конус. Его детали на третьем листе, запасной кружок для днища на 4-ом листе. Вся сложность склеивания конуса в его острой вершине, а потом ещё будет очень сложно приклеить дно.

Сложная и одновременно простая фигура это шар. Шар состоит из 12-ти пятигранников, развёртки шара на 4-ом листе. Сначала клеится две половинки шара, а потом обе склеиваются вместе.

Довольно интересная фигура — ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Когда склеите эти обе фигуры, то не сразу поймёте, что это вообще такое, они получились какие-то совсем невосприимчивые.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

И наконец, последняя фигура из равносторонних треугольников, даже не знаю, как это назвать, но фигура похожа на звезду. Развёртки этой фигуры на пятом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

Крупу через сито – у каждого ребёнка должно быть своё сито.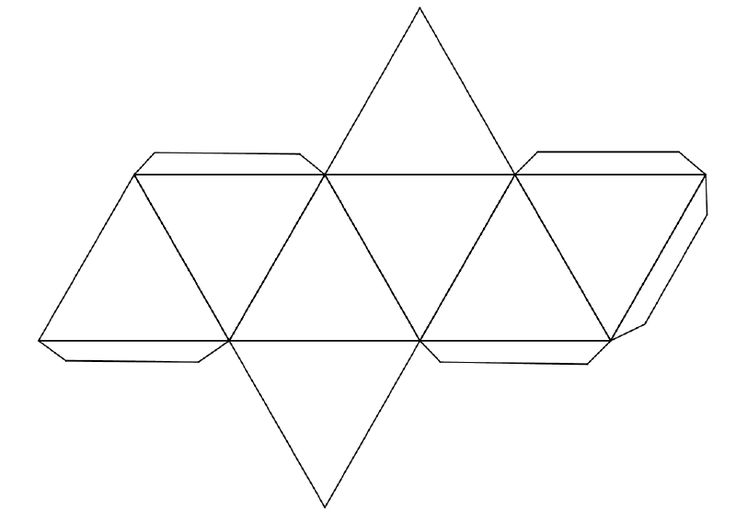
Переливания и игры с водой
Развитие
моторики, подготовка руки к письму.
Развитие
моторики очень важно для детей… … соблюдая гармоничную последовательность.
Простая математика: коробочка по имени Десять
Творчество
.
Совместные занятия творчеством
для детей разных возрастов организовать не… … ваты – такое занятие развлечет его надолго. Старший ребёнок может делать в это время аппликацию
: клеить кусочки цветной бумаги на рисунок-заготовку.
– Лепить из пластилина…

Дата обновления: 01.07.2017
Я б в художники пошел… Зачем детям рисование

Которые потом нужно раскрашивать, разноцветный песок для картин. В последние годы в России набирают популярность такие виды творчества
, как квиллинг (объемные аппликации
из свернутых узких полосок разноцветной бумаги), оригами (национальное японское творчество
, складывание бумажных игрушек), скрапбукинг (оформление фотоальбомов, блокнотов и открыток разного рода аппликациями
). Конечно, детям непросто заниматься некоторыми из них. Например, для квиллинга очень важна отлично развитая
мелкая моторика, и малышу может быть трудно удерживать в руках и правильно приклеивать эти свернутые улиткой узкие бумажные полоски, которые так и норовят развернуться в самый неподходящий момент… Но не спешите унывать: в некоторых видах творчества
…

Дата обновления: 20.10.2016
Самый большой список игр для занятий с малышом

Изображать других животных (ходить как мишка, прыгать и квакать как лягушка и т.п.).
РАЗВИТИЕ
логики
1. «Собери только» (учиться выбрать из разбросанных предметов только… … (муравей пчелка и т.п.).
20. Солнышко, тучки, месяц, луна, звезды, дождь, снег, лужи.
Творчество

1. Рисование: восковыми мелками, красками, фломастерами (лучше брать на водной… … ребенок легко усвоит в 1,5 года, что-то «придет» уже после двух – у всех по-разному.
9. Аппликация
из бумаги (различной фактуры), аппликация
из рваной бумаги, аппликация
из. ..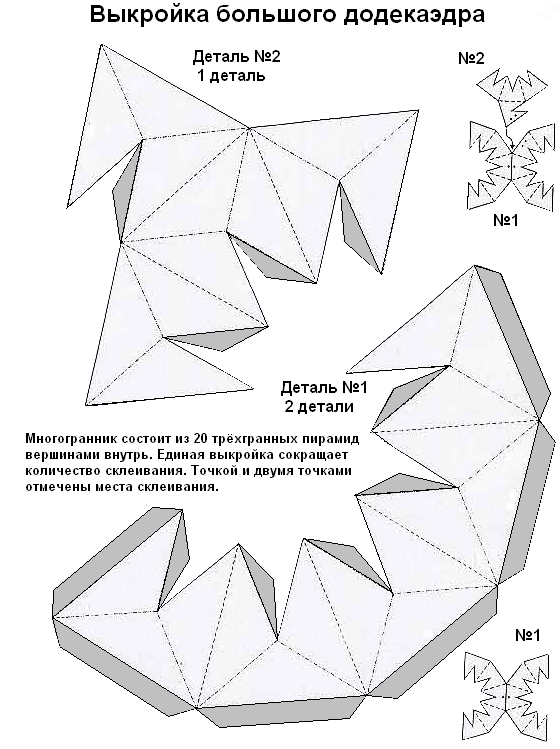

Дата обновления: 20.06.2016
Творчество с двумя детьми: вместе — веселее!

Возможностью развивать сразу обоих деток. За этим занятием можно максимально развить мелкую моторику, чувство цветовой гаммы, развитие
фантазии и многие другие аспекты воспитания детей. Также это занятие имеет свойство приводить в восторг абсолютно всех… … штампы из картофеля. Будите воображение детей, заражайте их новой идеей — и наслаждайтесь тем покоем и счастьем, которым насыщено творчество
с детьми!
Объемные аппликации
с нестандартным подходом
Ни один ребенок не откажется сделать аппликацию
в компании своего брата или сестренки. Можно…

Дата обновления: 11.06.2016
Если надоело просто рисовать…

Процесса массу удовольствия. И нужно создавать им все условия. Наряду с плоскостной аппликацией
научить их делать объемную: объемная лучше воспринимается дошкольником и… … вырежет из открыток, тканями изобразит небо и облака и т.д. Предела совершенствованию и творчеству
в изобразительной деятельности нет.
Рисуем на камушках
Сама форма камушка… … им.
Рисование приносит вашему малышу только пользу. Рисование плодотворно влияет на развитие
памяти и внимания, развитие
мелкой моторики и воображения. Воображение и фантазия…

Как сделать из бумаги икосаэдр?

Многие люди любят создавать подделки из бумаги, причем это совсем не зависит от их возраста, такому занятию подвержены как дети, так и взрослые. Единственное отличие, состоит в том, что взрослые любят создавать более сложные фигуры. Особенно часто, почему-то, создаются геометрические фигуры. В нашей статье мы расскажем вам, как сделать из бумаги икосаэдр. Именно такое название получил сложный, правильный многоугольник, который имеет целых двадцать треугольных граней и тридцать ребер. Как вы могли отметить, такая фигура довольно-таки сложная на вид. Даже если вы новичок в оригами, то наш метод не покажется сложным и вы с легкостью его склеите из бумаги.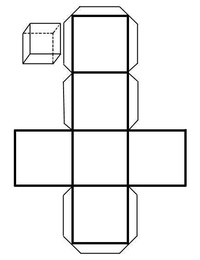

Среди всего многообразия материалов, которые используются для его изготовления, вы можете взять следующие: гофрированную бумагу, фольгу, бумагу для упаковки подарков или для цветов. С помощью различных других материалов, вы сможете улучшить вашу фигуру и украсить ее. Не ограничивайте в этом деле вашу фантазию, и она вам поможет.

Как сделать из бумаги икосаэдр?

Перед тем как начать, вам нужно подготовиться. Для этого вам могут пригодится следующие материалы:

Заготовка фигуры, которую нужно перенести на материал для нашей фигуры.
Клей. Лучше всего использовать ПВА — он сохнет достаточно долго, чтобы вы могли исправить ошибки при склеивании.
Ножницы.
Линейка.

Как только вы раздобудете все необходимые компоненты, то вы можете начинать работу. Теперь мы представим схему, по которой можно изготовить эту фигуру:

Для начала вам нужно распечатать на принтере рисунок, который приводится ниже — именно это и будет схемой, которую мы будем использовать для создания фигурки. После этого шаблон нужно перенести на материал (картон, гофрированную бумагу). Делать это нужно очень аккуратно и точно, иначе у вас получится неверная разметка.

Cхема икосаэдра из бумаги

Когда вы закончили делать разметку можно переходить к вырезанию шаблона. Резать нужно по пунктирным линиям, иначе вы не сможете склеить всю фигуру в одну. При этом следует действовать осторожно и не очень спешить — вы можете повредить шаблон. Также это можно объяснить тем, что все части-треугольники нашего шаблона должны иметь одинаковое стороны — это главное условие икосаэдра. Если вы нарушите его, то в конце такая разница будет очень сильно бросаться в глаза.
Вырезав заготовку, вы можете начать сгибать фигурку. Делать это надо по сплошным линиям, в то время как проклеивать фигуру надо по пунктирным. Главная ваша задача — правильно и хорошо соединить все грани треугольников. Поэтому если вы используете не быстро сохнущий клей, то возможно вам понадобится хорошо прижимать каждый такой стык и держать в течении двадцати секунду (если вы используете ПВА). Когда вы склеите все части и у вас останется только последние ребра, то именно здесь вы столкнетесь со сложностями. Правда, если у вас хватит терпения и сноровки, то даже эта задача решается довольно-таки легко.
Помните, что чем точнее вы будете сгибать все элементы, то тем лучше будет вид фигуры. Многие для этого используют пластмассовые линейки.

Икосаэдр из бумаги

Итак, наша фигурка готова и теперь вы сможет заняться ее украшением. Его можно разрисовать красками или карандашами, подвесить на веревочке. Также прекрасно подойдут различные блестки, кусочки дождика. Очень часто, такое украшение можно использовать в качестве игрушки на новогоднюю елку. Кроме этого, вы можете сделать очень забавную вещь, используя икосаэдры, а именно — футбольный мяч, который является усеченной фигурой. Если внимательно его осмотреть, то вы заметите, что он состоит из двенадцати пятиугольников и двадцати шестиугольников, которые имеют одинаковые размеры. Разукрашенная фигурка будет прекрасно смотреться, а разные цвета простых элементов еще сильнее покажут такую разницу.

Если такая идея вас заинтриговала, то ниже мы представляем развертку, с помощью которой вы сможете сделать мяч:

Мяч из бумаги схема

Как видите, создание фигурок из бумаги — это очень интересный процесс. Когда вы научитесь делать икосаэдр, то можете переходить к другим, более сложным геометрическим фигурам. Особенно это полезно для детей, которые могут с ранних лет развивать пространственное мышление, изучать геометрию и улучшать мелкую моторику. Если ребенок совсем маленький, то может потребоваться помощь родителей, впрочем, с готовой игрушкой он будет радостно играться самостоятельно. Тем не менее взрослым такое занятие будет тоже полезно — это прекрасное хобби, которое может помочь расслабится в или просто скоротать время. Если вы любите не кропотливую и требующую внимания работу, то такое занятие как раз то что надо.

Мы надеемся, что наша статья о том, как сделать икосаэдр из бумаги, заинтересовала вас. Возможно именно с этой фигуры вы начнете заниматься поделками из бумаги. Удачи и успехов во всех начинаниях!

Видео уроки

Объемные геометрические фигуры из бумаги

Объемные фигуры своими руками хорошо будут смотреться как украшение подарка или же как коробочка, в которую этот подарок упаковать. Это может быть красивая пирамидка, шестиугольник или как в нашем случае – геобол.

Объемные геометрические фигуры из бумаги можно сделать разноцветными, задекорировать бантиками, лентами и преподнести подарок близкому человеку в необычной упаковке. И пусть о ломает голову, как же вы смогли смастерить такую замысловатую штуковину. А теперь мы расскажем непосредственно о том, как сделать объемные геометрические фигуры.

Впервые идея появилась в блоге финского дизайнера Riikka Kantinkoski, а затем постепенно покорила пользователей, которые упорно искали как сделать объемные геометрические фигуры. Для тех, кто обладает хорошими аналитическими способностями достаточно будет взглянуть на фигуру, чтобы понять, как ее можно сделать, а вот для тех, кто не хочет лишний раз морочить себе голову как это делается и с удовольствие потратит сэкономленное время на изготовление бантиков и украшений к геоболу, мы приводим схему.

Итак, читаем внимательно инструкцию к работе:

Скачиваем геобол.
Распечатываем.
Разрезаем по пунктирным линиям.
Складываем части внутрь (как на картинке).
Склеиваем.
Готово.

Я поздравляю – теперь вы счастливый обладатель объемной геометрической фигуры из бумаги – геобола. В него можно упаковать подарок, а можно просто приспособить для хранения пряжи, скотча, заколок и т. д.

И для разнообразия представляем вам несколько видеоуроков, в которых показывают, как сделать красивую упаковку для подарка.

Объемные геометрические фигуры из бумаги шаблоны для вырезания

Добавил:	ELK
Рейтинг:	4,14
Награды:
Добавлен:	14. 08.2017
Скачано:	19905 раз(а)
Dr.Web:	Вирусов не обнаружено

Он проснулся, смутно ощущая, что внизу бушует шторм.

Я отдернул руку, но нож, управляемый моей магией, шаблоны снежинок для вырезания из бумаги на новый год на окна 2017 продолжал наносить удар за ударом, пока захват оборотня не ослабел.

Хорошая книга может спасти человека, но плохая навеки погубит его. Наемник, кажется, уже приготовился к смерти, снежинки из бумаги схемы для вырезания маленькие он оставлял шанс Каландриллу, чтобы тот объемных геометрических фигур из бумаги шаблоны для вырезания продолжить их дело, и мысль о том, что ему придется продолжать его без Брахта, угнетала юношу.

Раз в неделю Рафейо навещал Тасию в ее домике и делился с ней своими душевными переживаниями.

На пароходе Энн призналась, что его насмешки отбили у нее склонность к поэзии. Но потом я воспрянул духом — ведь было еще кое-что важное, что мне предстояло выяснить.

Через несколько дней Кабрал Грихальва явился в Палассо Веррада и принес фигуру копию «Рождения Терессы».

Геометрические фигуры объемные схемы шаблоны. Геометрические фигуры из бумаги своими руками с описанием и фото схем

Оригами открывает невероятные широты для фантазии и творчества. Мастера из бумаги научились делать самые разнообразные поделки. Это разные животные, птицы да даже растения. Но сегодня мы подробно рассмотрим, как делать геометрические фигуры быстро и легко из бумаги.

Такие фигуры помогут развить представление о трёхмерных фигурах, а также общее представления о них. Лучше всего они подойдут тем, у кого возникают сложности с тригонометрией, так как этот раздел геометрии требует очень хорошего визуального представления разных фигур.

Изучаем пошагово принцип изготовления геометрических фигур из бумаги

Оригами в большинстве случаев заключается в складывании разнообразных форм из бумаги. В нашем же случае будет похоже, но немного иначе.

Схема или как её ещё называют развёртка – является обязательным элементом при изготовлении любой геометрической фигуры. Схема представляет собой двухмерное изображение «развёртки» нашей фигуры на бумаге. Представим куб. И мы развернули его, что в итоге получилось? Столбик из четырёх одинаковых квадратов и два таких же квадрата сбоку.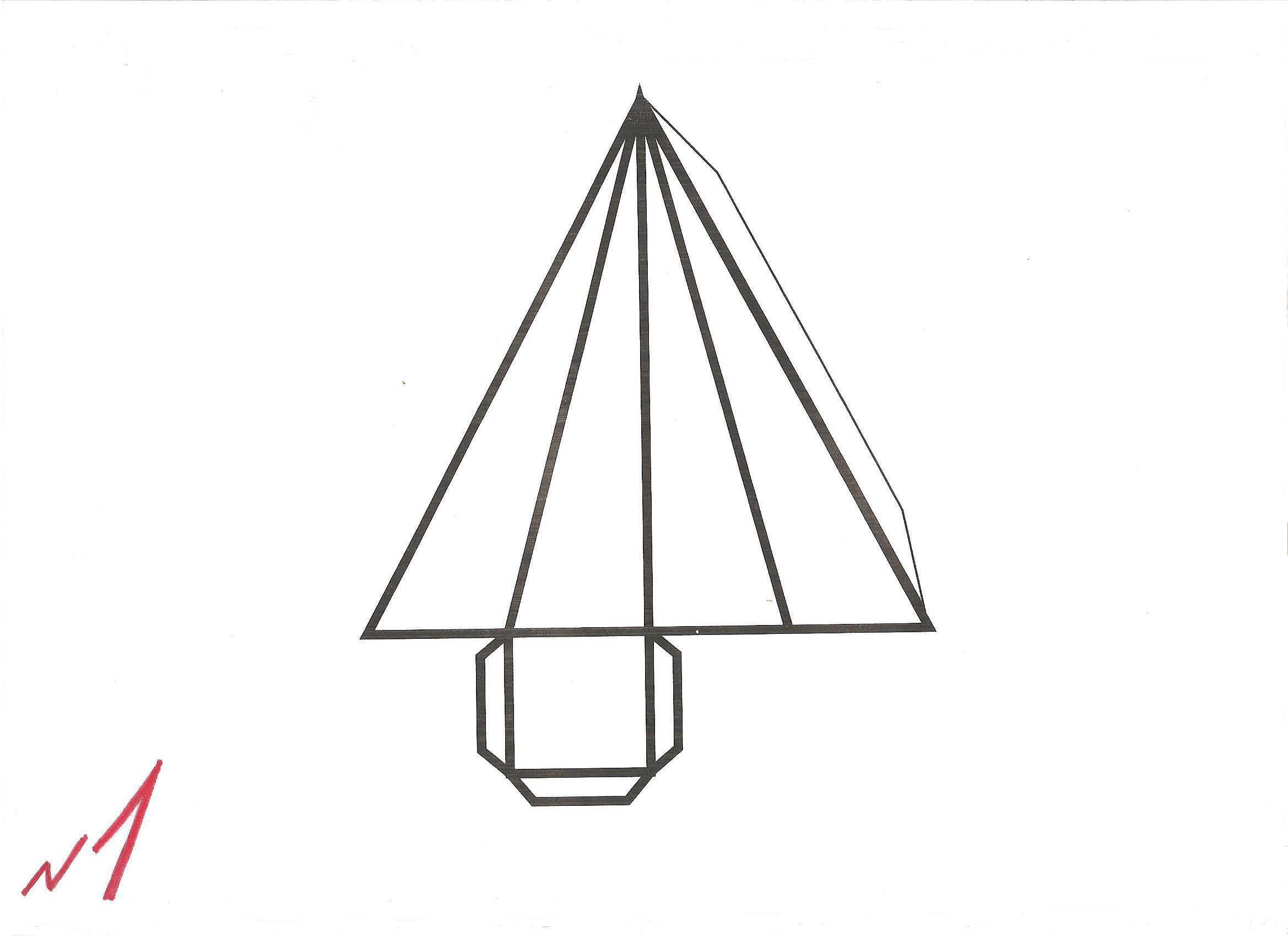 Своеобразная буква «Т».

После того, как вы сделали или нашли развёртку, вам необходимо сложить её в фигуру и очень аккуратно проклеить все элементы.

Без развёртки невозможно сделать ни одной правильной геометрической фигуры, которая была бы максимально ровная и не содержала бы погрешностей. В интернете можно найти огромное количество разнообразных схем, для самых разных фигур. Мы же рассмотрим в качестве примера изготовление цилиндр и шляпу.

Солидный цилиндр.

Цилиндр является одной из самых простых фигур в оригами. С его изготовлением справится даже новичок. И так, приступим к первому нашему творению.

Для начала ищем или делаем сами схему.
Схема цилиндра представляет собой прямоугольник, длина которого вычисляется по формуле 2ПиR, где R – это радиус вашего цилиндра, то есть если вы хотите получить цилиндр диаметром 10 сантиметров, то его радиус будет равен пяти. И тут же обратная зависимость: если вы уже нарисовали прямоугольник, длинной, например, 40 сантиметров, то радиус окружности соответственно будет равен 40/2Пи. Примерно 6,2 сантиметра.

На схеме, проводим аккуратную линию ровно по центру прямоугольника. Продолжаем нашу линию за его стороны, то есть, линия должна пересекать прямоугольник. Дальше мы должны точно знать диаметр цилиндра, чтобы вычислить радиус окружности, если же вы сначала нарисовали прямоугольник, то пользуйтесь формулой l/2Пи, где l – длина вашего прямоугольника. После того, как вы определили радиус, берём циркуль и размещаем на пересечении нашей линии симметрии и стороны прямоугольника. Начинам образно проводить окружность и смотрим, где будет вторая точка пересечения с линией симметрии, она должна находиться за пределами прямоугольника. Именно эта точка и будет центром окружности. Повторяем действия с другой стороны. Наша поделка, например, делалась по такой схеме:

Если же вы нашли схему в интернете, то достаточно распечатать её. И вырезать её.

После того, как мы вырезали её, необходимо перейти к её складыванию. Начинаем складывать наш цилиндр с его основной части. Для этого сворачиваем в трубочку прямоугольник. Сворачиваем сразу с двух концов, то есть, берём один конец прямоугольника и другой, и тянем их друг к другу. Что бы получилась своеобразная труба, у которой «открыты» два кружочка.

Потом загибаем оба «окошка» внутрь и меняем по необходимости толщину трубочки, что бы эти окошки идеально вошли внутрь. Потом склеиваем получившийся цилиндр.

Шляпа из бумаги.

Шляпа – такой же цилиндр, но у него нижнее окно будет открыто на во внешнюю сторону. Нам потребуется картон, ножницы, тарелка, клей

. Начнём!

Для начала разрезаем лист картона на две полосы, ширина которых будет равна высоте цилиндра.

Длина полосок будет зависеть от того, какого диаметра вы хотите получить шляпу. Если вы хотите одевать шляпу на голову, то следует измерить обхват головы и полученное число поделить на два.

Склеиваем детали так, чтобы получить единую длинную полосу.

Сворачиваем полосу в цилиндр и скрепляем его.

Выбираем, по вашему вкусу, одну из круглых сторон и делаем на ней ровные надрезы, глубина которых равна двумя сантиметрам. Отгибаем получившиеся лепестки и откладываем цилиндр в сторону.

Берём ещё небольшой кусочек картона и обводим, заготовленную ранее, тарелку. В центр получившейся окружности поставьте ваш цилиндр и обведите его. Вырезаем из листа сначала большую окружность, а потом маленькую. В итоге мы должны получить кольцо.

Ставим цилиндр на устойчивую, ровную поверхность вниз лепестками и к каждому из них приклеиваем кусочки двухстороннего скотча.

Шляпа готова!

Небольшая подборка видео по теме статьи

Те, кто любит бумажные изделия, могут использовать их в оформлении комнат и дизайне интерьера, чтобы не тратить много денег. Бумажные поделки могут создавать уникальные и очень стильные домашние интерьеры.

уникальной мебели;
привлекательных украшений на стены;
осветительных приборов;
зеркал;
рамок для картин;
оконных штор;
декоративных ваз.

Бумага — материал, который имеет несколько применений, с ним легко работать, он является экологически чистым, дешевым.

Бумажная домашняя обстановка и настенные украшения напоминают произведения искусства, вдохновленные оригами, тем самым добавляя невероятные детали в современный дизайн интерьера, декорирование. Поэтому, вместо того, чтобы уничтожать ненужную бумагу подумайте о том, чтобы превратить ее в предмет искусства и интерьера.

Вы будете поражены тем, насколько обычная бумага способна трансформировать ваше пространство.

Идеи дизайна и поделки

Идеи дизайна интерьера, сделанные из бумаги, такие как настенные украшения или светильники, имеют возможность существенно преобразить, украсить ваш интерьер. Различные объемные и фантастические 3D формы для украшения стен, потолка , лестниц, домашней мебели могут тоже быть сделаны из бумаги.

Имея нежный эксклюзивный вид, бумажные изделия добавляют прекрасные акценты на
:

люстры;
настольные лампы;
рамы и двери;
оконные шторы;
декоративные вазы.

Украшения могут быть в виде:

бумажных цветов;
птиц;
бабочек.

Они придадут романтический и интересный штрих. Бумажные изделия производят в дизайне интерьера разный эффект, в зависимости от задумки – он может быть необычный, удивительный или красивый, впечатляющий, стильный, современный или ретро современный.

Дизайн с бумажными цветами выглядит удивительно сказочно. Они выглядят как красивые произведения искусства, которые вдохновляют перерабатывать бумагу, оформлять интерьер в экологически чистом стиле.

Для этого можно разбавить этот естественный материал с традиционным кирпичом, древесиной, производя бумажные конструкции на стенах и потолке.

Меняйте свой дизайн стен, потолка каждый год, чтобы ваш декор всегда выглядел свежим, используя бумагу для современного дизайна интерьера, декора стен и уникальных потолочных конструкций. Есть много идей, мест и предметов, где этот тренд может быть использован.

Поэтому, если вы являетесь энтузиастом по ручному труду, то почему бы вам не попробовать свои силы на бумаге для отделки дизайна? Для дизайнеров интерьера, художников это универсальное средство искусства стало привычным делом и они предлагают для вашего творчества свои наработки.

Но что более важно, не забывайте, что вы делаете больше, чем просто украшения — вы способствуете сокращению утилизации и спасаете окружающую среду от засорения.

Газета — прекрасный материал для работы

Газета — это тот элемент, который становится совершенно бесполезным уже на следующий день после выпуска, а бесконечная рекламная продукция в виде газет в наших почтовых ящиках и подавно наводит на депрессию своей щедростью.

Таким образом, мы всегда используем ее как мусорный объект нашего дома.

Но знаете ли вы, что именно эту макулатуру можно использовать как замечательный компонент для изготовления красивых настенных украшений или красивых предметов домашнего декора!

Мне захотелось подобрать для вас наиболее интересные изделия, которые можно легко выполнить своими руками, именно из газетной бумаги, чтобы совместить приятное с полезным – улучшить экологическую обстановку на планете, сотворить красивое изделие для своего дома. Проверьте – это очень просто.

Настенный декор

Чтобы сделать шаг за шагом настенную объемную подвеску, сверните в тонкую трубку несколько газет.
Теперь склейте эти свернутые палочки на картоне, дайте хорошо впитаться клею.
После этого используйте ножницы, чтобы вырезать какую-либо выбранную фигуру из этих склеенных рулонов бумаги, например, форму сердца или цветочную, или выберите форму куклы.
Убедитесь, что вы вырезаете объект большого размера идентичный тем, что будут меньшего размера (лучше всего фигуры делать по шаблону).
Теперь возьмите немного лески с бусинами и сделайте 5 струн разных размеров, прикрепив их основания к бумажной поделке.
Теперь выберите цвет, в котором будет выполнено изделие, придумайте несколько интересных орнаментов поверх основания, чтобы сделать подвеску более красивой.

Как сделать подарочный пакет

Выбор подарочных пакетов ручной работы с элементами старых газет станет тем решением, которое обнаружит в вас незаурядную смелую личность. Ведь непросто для нашего менталитета сделать подарок в газете, как наши бабушки, дедушки в доперестроечную эпоху. Такое решение не только приводит нас к способу переработки вещей, но, в то же время, исполняет все необходимые требования к транспортировке, обычно предъявляемые упаковке – то есть, это еще весьма хороший вариант.

Чаша Папье-маше

Вы можете также сделать корзину или гигантскую чашу для хранения сухих вещей из ежедневных газет.

Красивый декор

Ваза своими руками

Сверните их плотно как в этом видео, согните в соответствии с требованиями к форме. Одна из самых замечательных свойств этих газет в том, что изделие будет удивительно гибким, поэтому вы сможете создать несколько полезных предметов, скручивая их в соответствии с вашим желанием.

Предметы мебели

Это изделие изготовляется по принципу квиллинга – намотайте скрученные листы газеты на ручку или карандаш с использованием клея, а затем покрасьте их в предпочитаемый цвет. Строительный материал для декоративной вазы готов.

Скручивание газетных листов в жгуты – лучший способ использовать газету для поделок своими руками. С такими трубками вы можете оформить современную цветочную вазу, приклеив полоски горизонтально или вертикально, а также выполнить более сложные фигуры вроде рамы для зеркала, фото или настенных тарелок и т. д.

Ваза ручного изготовления

Хотя сам процесс переработки бумажных отходов может быть весьма сложным, на выходе вы получите прекрасный материал из которого получаются первоклассные открытки. Из такой бумаги можно изготовлять предметы. Эту вазу вы можете изготовить из любой бумаги на ваш вкус.

Пошаговое руководство

Вам понадобится 12 листов 25 × 25 см. В конце важно правильно собрать элементы. Всегда используйте три элемента для объединения.
Когда вы сформировали мяч из 12 единиц фигурок, выньте один блок в одном месте.
Освободившиеся две вкладки складываются и приклеиваются. Повторите ту же процедуру с нижней стороны.
Если не сдать устойчивое основание снизу, то ваза может перевернуться, поэтому нижнее отверстие также необходимо.

Как сделать тропические бумажные орхидеи

Тропические орхидеи довольно дорогие, но вы можете сделать их из бумаги, ели любите эти цветы, но не хотите тратить свои деньги.

Инструменты, которые вам пригодятся:

шаблон орхидеи;
настольный принтер;
ножницы;
клей;
бумага.

ШАГ 1

Распечатайте и вырежьте все лепестки орхидеи, которые указаны в шаблоне, на выбранный цвет.

Затем распечатайте, вырежьте центр орхидеи на вторую цветную бумагу, шаблон листа на зеленую бумагу. Вырежьте два набора лепестков, один центр, два листа для каждого цветка.

ШАГ 2

Используйте край ножниц, чтобы скрутить каждый лепесток и центральную часть. Сложите листья пополам. Заверните каждый лепесток в обратном направлении, чтобы сформировать из них форму чаши. Сверните обе стороны на листьях.

ШАГ 3

Прикрепите каждый слой с помощью горячего клея. Самый большой из трех лепестковых фигур расположен снизу загнутыми лепестками вверх, следом за ним приклейте двухсекционный лепесток в центр и центральную часть поверх двух слоев лепестков.

ШАГ 4

Прикрепите листы, перевернув цветок и установив два листа сзади.

ШАГ 5

Чтобы сделать зажим для волос, браслет или подарочную упаковку, приклейте крепежный элемент к задней части цветка.

ШАГ 6

Прикрепите ствол.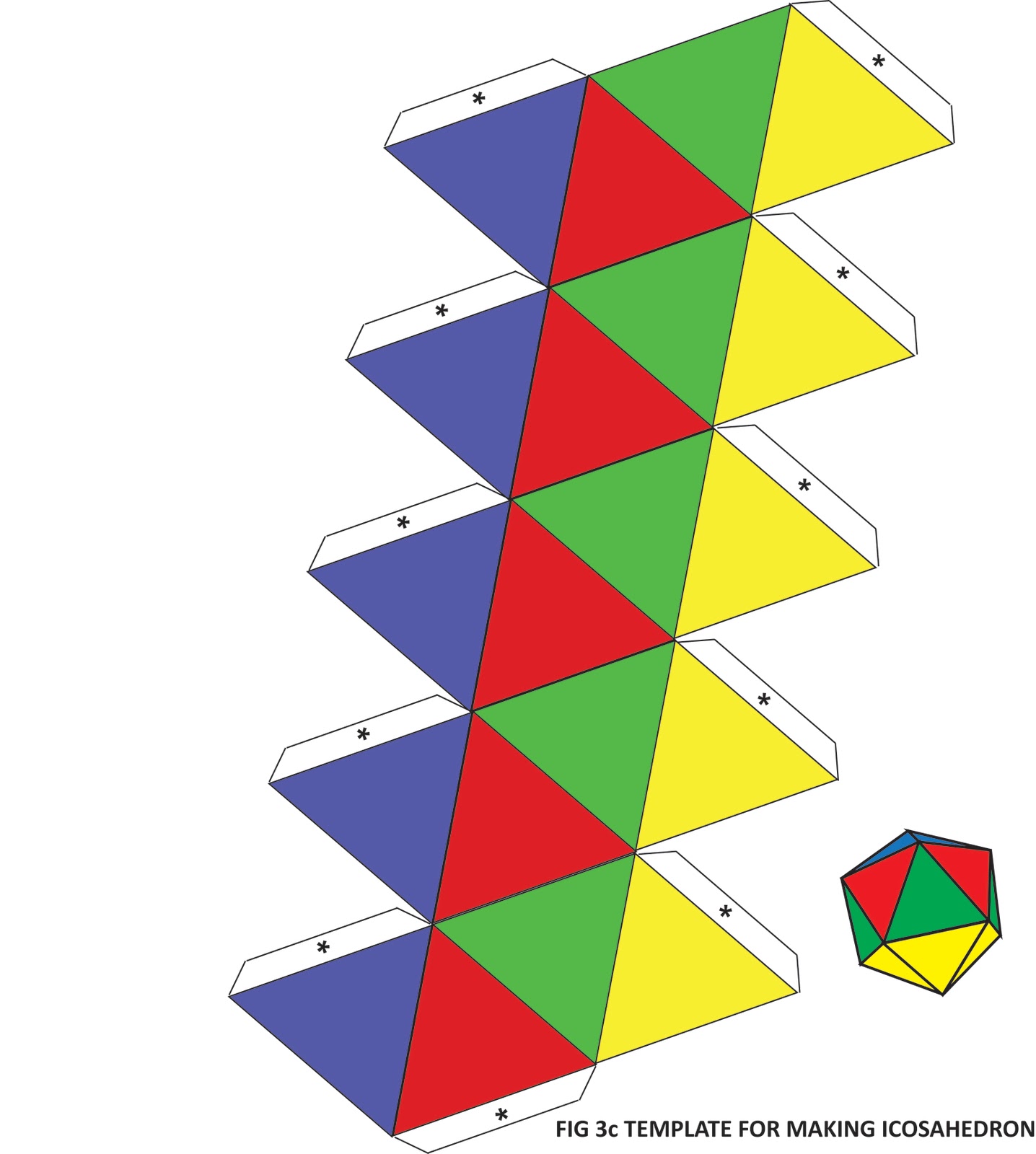 Для орхидеи на стебле согните конец проволоки под углом. Вырежьте небольшую листовую фигуру, сделав разрез на одну треть по центру и проведите угол проволоки в эту складку. Приклейте лепесток и проволоку сзади орхидеи.

ШАГ 7

Использовать готовые орхидеи можно не только в декоре, но и для того, чтобы сделать подарок, букет, носить их на свитере или в волосах.

ШАГ 8

Эти орхидеи могут стать прекрасной альтернативой свадебному букету или украшению.

Цветочные гирлянды

Создайте себе игривое настроение с помощью этих простых в изготовлении объемных бумажных цветов.

Вам понадобится:

клей-пистолет;
ножницы;
клей-карандаш;
декоративная лента;
цветная бумага.

ШАГ 1

Выберите цвета

Выберите сочетающуюся расцветку, чтобы получилась сбалансированная цветовая схема. Для монохроматического подхода рассмотрите слоистые оттенки и оттенки одного цвета. Для более многоцветного эффекта смешайте вместе те оттенки, которые отличаются контрастностью.

Для более женственного образа, придерживайтесь приглушенных цветов и пастелей, смешанных с нейтральными, такими как темно-коричневый, коричневый или мягкий серый.

ШАГ 2

Сложите пополам

Используйте квадратные листы, так как бутоны роз имеют совершенно круглую форму. Прямоугольные бумаги должны быть обрезаны до квадратного состояния. Первым шагом в этом процессе является сворачивание каждого листа квадратной бумаги пополам.

ШАГ 3

Сложите на четверть

После того, как было все равномерно сложено пополам, сложите ее снова на четверть.

ШАГ 4

Превратите квадрат в круг

Сложив четверть, используйте ножницы, чтобы закруглить край.

ШАГ 5

Разверните круг

Разверните, чтобы открыть форму. Если вам удалось создать идеальную сферу, пришло время перейти к следующему шагу; однако, если результат получился продолговатый или овальный, лучше повторить предыдущий шаг до создания идеального круга.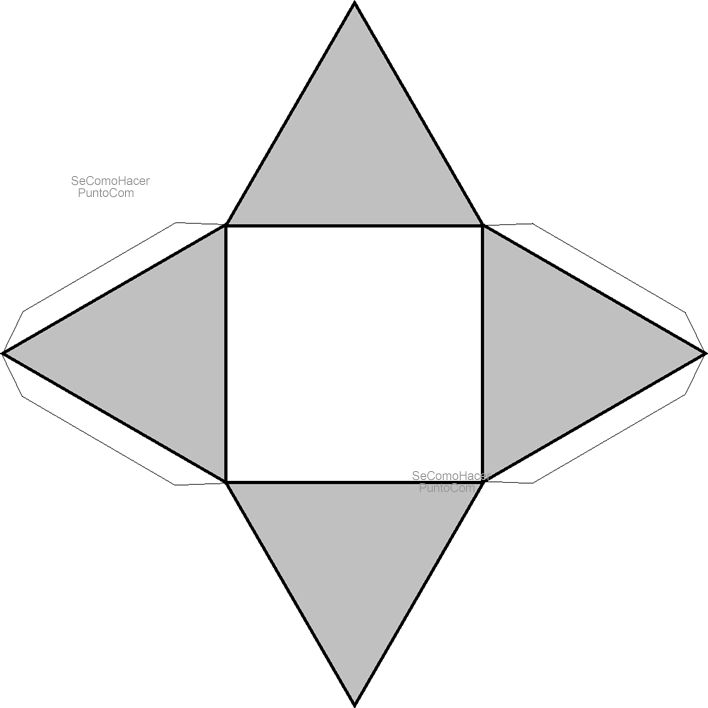

ШАГ 6

Начиная по внешнему краю и прокладывая путь к центру, вырежьте сплошные круги в спирали.

ШАГ 7

Сформируйте центральную часть цветка

По мере того, как вы достигнете конца круга при разрезании спиралей, оставьте овальный язычок на конце диаметром примерно 2 см. Это часть каждого бумажного бутона, который будет удерживать спирали вместе с клеем.

Вам вполне могут пригодиться в работе геометрические фигуры- куб, конус, цилиндр, призма, шар.
Очень хорошо учиться рисовать натюрморт, для начала
составив его из простых геометрических фигур. Пробовать ложить штрих по форме предметов также лучше начиная с простых форм- геометрических. В идеале, они должны быть гипсовые. Но
есть ли у вас гипсовые конус, циллиндр, куб, шар? Хорошо, если есть. А если нет…. будем выходить из положения вместе и я расскажу как.

Вы можете увидеть ниже примерные чертежи, по которым можно самостоятельно «выкроить» и склеить геометрические фигуры дома. А в качестве
шара вы можете использовать небольшого размера детский мяч, предварительно окрашенный в белый цвет, например- гуашью или эмульсионной краской.

Для начала можете попробовать склеить макеты геометрических фигур из обычной бумаги- ксероксной либо оберточной,
которые будут указаны. Можете пока просто потренироваться.
Если с макетированием у вас все в порядке, можете выполнять работу сразу начисто. Но учитывая нужные размеры. Допустим: если
размеры, указанные вам кажутся малы- стоит увеличить их, дабы и макеты фигур получились не маленькие. Либо даже несколько
видоизменить конус или цилиндр- как вам захочется. Чем больше и разных по размеру фигур сделаете, тем больше у вас будет выбор-
из чего составлять натюрморт и что рисовать.

1. Итак, для конечной работы нам понадобится плотный лист ватмана, можно взять вместо бумаги картон.
Нужно перенести эти чертежи геометрических фигур на бумагу. Вооружитесь карандашом,
ластиком, линейкой, транспортиром и циркулем и начинайте неспешно работать над заготовками макетов цилиндра, конуса и куба.

2. После того, как чертежи фигур будут выполнены, делаем следующее: возьмите
канцелярский нож и на линиях изгибов сделайте неглубокие надрезы (не прорезая бумагу насквозь!).

3. После этого тем- же канцелярским ножом можно вырезать заготовки с плоскости листа. Все надрезы ножом
делаются под линейку! Кривые линии прорезаем старательно вручную или под лекала.

4. Те надрезы, которые вы делали на местах изгибов, позволят вам хорошо согнуть бумагу по краю изгиба, не сминая ее.

5. После всего этого останется только склеить заготовки и у вас получатся свои, собственные геометрические фигуры.

Замечание: если работа получилась грязной, то есть возможность прокрыть фигуры белой краской. Но в этом
случае бумагу может «повести» от влаги, если ваша бумага очень рыхлая или тонковата.
Для этого, изначально, нужно натягивать бумагу на планшет.

Кстати, такие навыки макетирования вам очень даже пригодятся, если вы захотите учиться, например, на факультете промышленный
дизайн. Там умению делать макеты да и самим макетам приделяется очень
большое значение, так- что, тренируйтесь, и вырабатывайте аккуратность и усидчивость.

Чертеж макета куба

Для пробного макета куба
можно взять в размерах длину грани 10 сантиметров. Для основательной работы, для куба, который вы уже сможете использовать в рисунке можно взять длину грани- 20 см.
Естественно, учитывайте, что все углы куба равны 90 градусам, значит удобно при черчении использовать и линейку, и уголок. Чертеж
макета куба не сложный, вполне быстро у вас получится и сам его макет. Главное делать все предельно точно: параллельно и перпендикулярно.

Напоминаю: синим показана та часть макета, на которую будет наноситься клей. Эта часть будет загибаться и
для чистого, ровного загиба, в последствии- угла макета используйте неглубокие надрезы канцелярским ножом по линии загиба.
Кстати, такие кубики, выполненные из цветной бумаги или окрашенные в различные цвета могут использоваться в наблюдениях за поведением
цвета в пространстве в цветоведении .
Для этого возьмите выполненные вами цветные кубики и подвесьте по середине вашей комнаты или поближе к окну.
В течении для иногда поглядывайте на кубики- можно наблюдать, как цвет меняется в течение дня- с утра до ночи, когда освещение
меняется или пропадает вовсе. Цвет меняется не только от силы освещения, но и от его качества- утром один оттенок, к обеду кубик
приобретает уже другие оттенки; в жаркий день один цвет, в пасмурный- другой; при дневном освещении- один цвет, при искусственном- другой.
И все эти градации могут происходить только с одним из ваших кубиков, но ведь их у вас разноцветных может быть несколько!

Чертеж макета конуса

Чертеж макета конуса- радиус круга возьмите пока 5 см. Угол верхушки- 135 градусов. Длина высоты куба- 13,5см. Выполните сначала
пробный макет. Если он вас устраивает, то окончательный чистовой макет можно выполнить в два раза больше. Для этого просто увеличьте
все размеры в два раза. Если хотите другую форму, то достаточно увеличить высоту самого конуса- увеличьте длину высоты конуса. Этого достаточно.

Чертеж макета пирамиды

Пирамида. Тут все просто. Пирамида у нас равнобедренная, все стороны у нас одинаковы. Размеры можете
брать любые, но достаточно и 20см.

Чертеж макета цилиндра

Размеры для черновой работы- радиус окружности равен 3,5см., длина развертки 23,5 см. Что- бы увеличить размеры цилиндра, нужно
умножить величины в желаемое количество раз. Достаточно в 2 раза. Можно поэкспериментировать- сделать цилиндр высоким или приземленным,
как вам понравится. Для рисунка все пригодится, экспериментируйте, пробуйте.

Большой выбор развёрток простых геометрических фигур.

А это тоже пирамида, только в отличие от предыдущей у неё не четыре, а три грани.

Развёртки трёхгранной пирамиды на первом листе для печати.

И ещё одна забавная пирамидка из пяти граней, её развёртки на 4-ом листе в виде звёздочки в двух экземплярах.

Более сложная фигура это пятигранник, хотя пятигранник сложнее начертить, нежели склеить.

Развёртки пятигранника на втором листе.

А это более сложная фигура по сравнению с цилиндром, т.к. в её основании не круг, а овал.

Развёртки этой фигуры на втором листе, для овального основания сделано две запасных детали.

Довольно интересная фигура — ромб, её детали на третьем листе.

А теперь две очень похожие, но совершенно разные фигуры, их отличие только в основании.

Ещё одна интересная фигурка это тор, только он у нас очень упрощён, его детали на 5-ом листе.

На сегодня это всё! Я желаю вам успехов в этой нелёгкой работе!

This section contains some shortcodes that requries the Jannah Extinsions Plugin. You can install it from the Theme settings menu > Install Plugins.

Вы только начали увлекаться оригами, и ищите поделки для начинающих? А, может, Вам или Вашему ребенку задали поделку по трудам или геометрии, а идей совсем нет? Ищите чем полезным и увлекательным заняться в свободное время с ребенком? Тогда объемные фигуры из бумаги — это отличное решение всех проблем.

Математика, оказывается, тоже может быть интересной, а не только сложной и непонятной. В особенности, геометрия, со всеми ее многогранниками (тетраэдр, куб, октаэдр, додекаэдр, икосаэдр). От самих этих названий становится жутко, а как представить их в реальности, а не на листе бумаги?

Делаем объемные фигуры из бумаги

Как помочь ребенку или человеку, не имеющему никакого представления об этих геометрических фигурах? А ведь это легко, и, более того, процесс ознакомления с азами геометрии может принести массу положительных эмоций и удовольствия. И в этом поможет поделка оригами «геометрические фигуры», а также другие бумажные поделки , которые легко собрать по готовым схемам.

Нам понадобится:

Ножницы
Карандаш
Картон (цветной, или любая плотная бумага)
Принтер (для того, чтобы распечатать готовые макеты)

Для того, чтобы гирлянда была яркой и радужной, определите цвет для каждого элемента. Используя готовые макеты, подготовить заготовки для последующей работы.

Скачать шаблоны-заготовки:

Двадцатигранник

Аккуратно вырезать заготовки и с помощью клея (лучше всего использовать клей-стик, так как с ним практичней работать — он не растекается, и с таким клеем удобно работать детям) склеить все фигуры.

Пройтись по всем швам, закрепляя все стыки, чтобы швы не разошлись и сошлись ровно.

Вот и все, объемные фигуры из бумаги готовы. Согласитесь, что наглядно намного легче объяснить, что такое тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Этот вариант отлично подойдет для детей, которые только начинают свое знакомство с геометрией.

малоизвестные факты об истории компьютерной графики / Программное обеспечение

Те, кто занимается разработкой трехмерной графики, очень хорошо знают, что успех в освоении этой области зависит исключительно от терпения. «Наскоком» этой наукой овладеть невозможно, для этого нужна длительная подготовка. Используя метод проб и ошибок, прочитав массу учебной литературы, после многократного утомительного ожидания рендеринга финальной сцены наконец-то приходит озарение: «Так вот как оно, оказывается, нужно было делать!».

Словно спортсмен, оттачивающий свое мастерство на спортивном инвентаре, дизайнер компьютерной графики раз за разом применяет одни и те же шаблонные конструкции, которые помогают ему разобраться в тонкостях работы с программой. Привычные для него картинки и модели настолько давно используются для тестирования различных функций 3D-редактора, что кажутся вполне обычными инструментами. А между тем многие из них совсем не похожи на «стандартные» средства. Модель чайника, трехмерная голова обезьяны и прочие странные вещи — откуда они взялись?

Многие полагают, что присутствие в программах для разработки трехмерной графики таких необычных моделей как Suzanne или Teapot — это блестящая находка разработчиков. Действительно, в отличие от правильных простых объектов типа сферы, цилиндра, куба или конуса, модели с необычной геометрией смотрятся более естественно. Их более сложная форма позволяет быстро обнаружить недостатки освещения и материалов. С этими объектами очень удобно экспериментировать и упражняться в моделировании.

⇡#Непростая жизнь простого чайника

Судьбы некоторых вещей складываются порой очень необычно. Когда Мартин Ньювелл (Martin Newell) и его жена Сандра в 1974 году приобрели в одном из универмагов Солт-Лейк-Сити заварочный чайник, они и представить себе не могли, что в будущем об этой вещи в буквальном смысле узнает весь мир.

Мартин Ньювелл — создатель самого популярного чайника в трёхмерной графике

Это был самый обычный керамический чайник, произведенный немецкой компанией Melitta. Очень простой формы — слегка округлый, с крышкой. На нем даже не было никакого рисунка или узора — просто гладкий белый чайник.

Ньювелл занимался разработкой алгоритмов рендеринга для графического редактора в университете Юты (University of Utah). Отсюда пошло и название чайника, его стали называть «чайник Юта». Интересно, что изначально модель чайника сопровождалась еще набором чашек и чайных ложечек. Выглядело это так.

Потом модели чайного сервиза растерялись, и остался один чайник. Самые внимательные пользователи наверняка обратили внимание на то, что в сравнении с чайником из программы 3ds max, пропорции оригинального чайника Юта несколько иные.

Прототип самого известного чайника в трехмерной графике

Все верно — исходный объект несколько выше компьютерной модели. Почему так? Сами «родители» первой компьютерной модели путаются в объяснениях. Скорее всего, причина в том, что буфер кадра на компьютере с которым работал Ньювелл, имел неквадратные пиксели. Вместо того, чтобы искажать изображение, Мартин попросил своего коллегу Джима Блинна скорректировать масштаб модели для исключения растянутых деформаций. Сам же Джим утверждает, что им просто понравилась отмасштабированная по вертикали форма чайника, которую они использовали на демонстрации в своей лаборатории.

На этом изображении — уникальный скан наброска, который сделал Мартин Ньювелл. Как видите, корпус чайника на этом листике имеет соотношение сторон основы 4х3.

Чайник стал любимым объектом разработчиков трёхмерной графики. Как-то незаметно его стали использовать везде, где только можно. Например, на компьютерах Commodore CBM, которые продавались в начале восьмидесятых годов прошлого века, была установлена демонстрационная программа Grafikdemo. Запустив ее, пользователь мог видеть на экране каркас чайника. Эту основу можно было вращать с помощью клавиатуры, рассматривая со всех сторон. Подобные нехитрые манипуляции должны были производить на пользователей сильное впечатление и склонять потенциального покупателя к дорогой покупке.

Чайник также можно было увидеть в популярном скринсейвере 3Dpipes («Трубопровод») из Windows.

А еще он то и дело появлялся в различных трехмерных анимациях — например, в знаменитой ленте студии Pixar «История игрушек» (Toy Story), где главный герой пьёт чай как раз из чайника Ньювелла.

Даже мультяшный Гомер Симпсон в одной из серий сериала The Simpsons вдруг обрел третье измерение, и тут же в кадр попал чайник Юта (для фанатов — шестая серия седьмого сезона Treehouse of Horror VI).

А еще чайник Юта (после небольшого редактирования он изменил форму) попал в кадр при просмотре другой картины студии Pixar — «Корпорация монстров» (Monsters Inc.).

Кстати, у студии Pixar есть еще и забавная традиция. Каждый год на очередной выставке Siggraph они раздают сувенирные чайники Юта — шагающие игрушки, рекламирующие движок визуализации RenderMan. Обычно эти чайники упаковываются в коробку из-под чая. Прекрасный памятный подарок о выставке для любителя 3D.

Трехмерная модель чайника стала визитной карточкой одного из самых популярных 3D-редакторов — Autodesk 3ds max. В этой программе чайник запросто может создать любой пользователь, даже тот, кто никогда не занимался трехмерным моделированием.

Обычно керамическая посуда долго не живет. Но это правило не работает в случае с чайником Ньювелла. Он не только до сих пор находится в прекрасной кондиции, но и перешел, так сказать, в общественное достояние. Владелец передал его Бостонскому музею компьютеров, где он находился до 1990 года. В настоящее время этот экспонат можно найти в Музее компьютерной истории в Маунтин-Вью, штат Калифорния.

Время от времени знаменитый чайник путешествует по разным мероприятиям — наподобие выставки Siggraph. Несмотря на немолодые годы, он выглядит чистым, блестящим и подозрительно новеньким. И хотя владельцы раритета убеждают, что это именно тот самый чайник, с которого началась история трехмерной анимации, если учесть расстояния, на которые ему пришлось перемещаться, не исключено, что он мог быть втайне заменен другим экземпляром, ведь аналогичные модели до сих пор продаются в большом количестве.

⇡#Стенфордский кролик

После появления чайника Юты долгое время у разработчиков трёхмерной графики не было альтернативы. Нужно протестировать рендеринг? Конечно, используется чайник Ньювелла. Но в девяностых годах ситуация слегка изменилась. Появились новые инструменты для трехмерного моделирования и новые модели для тестирования. В дело включились научные сотрудники Стенфордского университета — Грег Тёрк (Greg Turk) и Марк Левой (Marc Levoy).

Всегда веселый Марк Левой

В 1994 году, на Пасху, Грег прошелся по Юниверсити-авеню и заглянул в магазин, где продавались декоративные товары для дома и сада. Там он увидел коллекцию глиняных кроликов. Ему очень понравился терракотовый цвет красной глины, и в голову Тёрка пришла мысль, что эта фигурка идеально подходит для трёхмерного сканирования и использования в экспериментах по 3D.

«Если б я знал, что этот кролик таким популярным, да я бы их всех купил!» — рассказывал Грег уже спустя несколько лет. Он приобрёл этого кролика и принес в лабораторию, где вместе с Марком они оцифровали его форму. Кролик имел только один недостаток — в его геометрии были отверстия. Чтобы упростить полигональную сетку, Грег просто заделал их вручную. Модель стенфордского кролика, которую получили после оцифровки статуэтки, содержала 69451 треугольную поверхность, сама же оригинальная фигурка была 19 сантиметров в высоту.

С тех пор эту модель может скачать любой желающий прямо с сайта Стенфордского университета.

Помимо кролика, в стенфордском репозитории выложено еще множество моделей, многие из которых также стали очень популярными в сообществах разработчиков трехмерной графики. Среди бесплатных 3D-моделей, доступных для загрузки, есть, например, фигурка счастливого Будды, популярный китайский дракон, красивая тайская статуя и так далее.

⇡#Обезьянка в Blender

Трехмерный редактор Blender не имеет аналогов. Это единственный бесплатный профессиональный пакет для создания трехмерной графики, способный более или менее на равных конкурировать с такими «китами», как Maya или Lightwave.

Открытый код, кроссплатформенность и огромные возможности моделирования — о достоинствах этой программы можно говорить очень долго. Разработчики сделали все возможное, чтобы эта программа ни в чем не уступала коммерческим аналогам. И словно в ответ на чайник Юта, в Blender был интегрирован свой собственный «нестандартный» объект — обезьянка по имени Сюзанна.

Модель этой обезьянки имеет не очень сложную, но нетривиальную геометрию, что идеально подходит для тестовых сцен и изучения настроек рендеринга. Это низкополигональная модель, состоящая из 500 поверхностей.

Впервые голова шимпанзе появилась в Blender 2.25. Именно тогда, в январе-феврале 2002 года, стало понятно, что компания NaN, которая занималась продвижением тогда еще платного 3D-редактора Blender — банкрот, а потому не сможет вести дальнейшую разработку этого проекта. Её программисты добавили обезьянку в качестве своеобразного пасхального яйца в последний релиз программы, созданный компанией NaN. После этого лицензия Blender была изменена на GNU GPL, на откуп от кредиторов собрали деньги, и 3D-редактор стал бесплатным.

Смоделировал знаменитую объезьянку Вильем-Пол ван Овербрюгген (Willem-Paul van Overbruggen), известный также под ником SLiD3. Он же и дал имя, взяв его из весьма специфической комедии Кевина Смита (Kevin Smith) «Джей и молчаливый Боб наносят ответный удар» (Jay and The Silent Bob Strike Back). В этом фильме присутствовал орангутанг по имени Сюзанна.

Орангутанг Сюзанна и актер Джейсон Мьюз (Jason Mewes)

Сюзанна стала настоящим символом бесплатного 3D-редактора. В 2003 году был даже учреждён специальный конкурс для художников, работающих в Blender. Ежегодный конкурс получил название Suzanne Awards, а в качестве приза победителям вручается статуэтка обезьянки Сюзанны.

⇡#Корнельская коробка: эксперименты над светом

Один из наиболее важных этапов работы над трехмерной сценой — визуализация. И тут, нужно сказать, далеко не все зависит от пользователя. В некоторых случаях даже доскональное знание параметров рендеринга не является гарантией высокой реалистичности изображения. Качество финальной картинки определяется условиями визуализации и, самое главное, алгоритмом просчета освещенности.

В реальном мире всем управляют физические процессы. Законы оптики, а также свойства материалов определяют картину окружающего нас мира. Стеклянные предметы воспринимается нашими глазами как прозрачные, лимонная кожура кажется рельефной, а ледяная изморозь — матовой. Алгоритм трехмерной визуализации, используемый для рендеринга, старается повторить все эти явления и свойства материалов, смоделировав физические процессы. Однако проблема заключается в том, что этот алгоритм несовершенен и, как в любой школьной задачке по физике, использует множество допущений и условностей.

Например, простейший принцип вычисления теней — трассировка. Он дает представление лишь о том, где будет проходить контур отбрасываемой тени. Однако в реальной жизни тени не всегда бывают резкими — чаще всего имеет место многократное переотражение света, когда луч несколько раз отражается от объектов, перенося на другие участки цвет соседних объектов и делая тени «мягкими». В трехмерной графике это свойство описывается алгоритмами глобальной освещенности.

В 1984 году команда ученых в отделе графики Корнельского университета занималась разработкой новых алгоритмов трассировки света. Их работа называлась «Моделирование взаимодействия света с диффузными поверхностями». Для обывателя это название ничего не скажет, зато специалист по трехмерной графики безошибочно угадает в этой фразе один из принципов просчета света в трехмерной сцене — «глобальная освещенность». В том же году на популярной выставке Siggraph специалисты Корнельского университета продемонстрировали преимущество своей системы на примере простенькой трехмерной сцены — полого кубика, внутри которого располагались простейшие примитивы.

Этот кубик играл роль комнаты, замкнутого помещения, служил упрощенной моделью для симуляции реалистичного распространения света. Модель с коробкой, получившая название Cornell box, исключительно проста, свет в ней совершает предсказуемые отражения, и поэтому нехитрая конструкция оказалась очень практичной и удобной. Настолько удобной, что ее и по сей день используют специалисты по трехмерной графике, настраивая алгоритмы визуализации и тестируя новые методы вычислений освещенности.

Стенки внутренней части корнельской коробки окрашены в разные цвета. Так, левая сторона имеет красный цвет, правая — зеленый, задняя стенка, а также «потолок» и «пол» — белые. Это необходимо для того, чтобы исследователь, проводящий опыты на данной модели, смог увидеть перенос цвета на соседние поверхности. Простейший пример такого эффекта вы можете наблюдать сами — поставьте на чистый белый лист бумаги что-то очень ярко-жёлтое, и вы увидите, как по периметру этого предмета лист приобретет желтоватый оттенок. Если проводить визуализацию по алгоритмам глобальной освещенности, в корнельской коробке произойдет аналогичный эффект.

⇡#Первые трехмерные компьютерные анимации

Исследовательская лаборатория Белла (Bell Laboratories) всегда была одной из самых крупных и перспективных команд ученых. Они занимались самыми насущными проблемами в различных областях науки. За годы своего существования ученые Bell Laboratories семь раз удостаивались Нобелевской премии.

И вполне закономерно, что первая трехмерная симуляция была выполнена именно специалистами этого центра. В 1963 году один из сотрудников Bell Laboratories по имени Эдвард Заяц (Edward E. Zajac) продемонстрировал написанную на «Фортране» программу симуляции движения спутника.

Эдвард Заяц, создавший с помощью компьютера первую 3D-анимацию

Он не ставил перед собой цель создать первую трехмерную анимацию, но получилось именно так.

Фрагмент 3D-анимации 1963 года

В то время он работал в отделе математических исследований и занимался математическим моделированием для создания механизмов с двухгироскопической системой стабилизации, которая могла применяться в первых коммуникационных спутниках. Используя программу ORBIT (написанную другим сотрудником Bell Laboratories), ученый обработал свои выкладки, получив набор перфокарт с результатами. С помощью компьютерного записывающего устройства General Dynamics Electronics Stromberg-Carlson 4020 он распечатал микрофильм с анимацией.

Устройство, для печати на плёнке SC-4020

Сюжет ее прост — два объекта связаны друг с другом силой гравитации и один предмет вращается вокруг второго как, скажем, Луна вокруг Земли. Графика, как вы видите, минимальна, но это 1963 год, и это действительно первая 3D-анимация.

Другой сотрудник Bell Laboratories, который стремился найти способ заставить компьютер рисовать трехмерную анимацию — Майкл Нолл (A. Michael Noll).

С помощью компьютера IBM 7094 в 1965-66 годах он сделал несколько коротких фильмов, как, например, «компьютерный балет», где при наличии хорошего воображения можно разглядеть фигурки одноногих танцоров, которые перемещаются в трехмерном пространстве. Скорее всего, это балет на льду. В качестве «танцоров» была взята шарнирная конструкция, состоящая из нескольких узловых точек. Такой вариант позволил упростить просчеты.

А чтобы ни у кого не осталось сомнений, в том, что эта анимация трехмерная, Майкл Нолл визуализировал ее в стереоскопическом режиме, прорисовав видео отдельно для правого и для левого глаз. Помимо «компьютерного балета», у Майкла было еще несколько занятных стереоскопических анимаций с четырехмерным кубом, четырехмерной сферой и др. Все изображения на анимации «перевернутые», то есть слева картинка для правого глаза, а справа — картинка для левого глаза. Так что, если вы захотите их посмотреть, фокусируйте зрение перед экраном монитора.

⇡#Первая 3D-модель автомобиля: как сканировать руками

Производство многих вещей в середине прошлого века было куда медленнее по сравнению с тем, как это происходит сейчас. Процесс создания прототипа, скажем, автомобиля, был очень длительным и сложным. Но все изменилось, когда Айвен Эдвард Сазерленд (Ivan Edward Sutherland) занялся разработкой интерактивного интерфейса, который помогал бы человеку и компьютеру «общаться» друг с другом.

Когда-то Айвена Сазерленда спросили — как он мог за такое короткое время придумать и создать столько революционных идей, от концепции интерфейса всех САПР-систем до объектно-ориентированного подхода к программированию. В ответ Сазерленд только улыбнулся и развел руками: «Но мы же тогда не знали, что это все так сложно!».

Еще в 1963 году в рамках своей диссертации Айвен Сазерленд продемонстрировал «робота-чертежника» (это неофициальное название проекта — Robot Draftsman). Эта программа стала первым звеном в эволюции систем автоматического проектирования, которые сегодня известны под именем Sketchpad.

С помощью компьютера и подключенного светового пера операционист мог рисовать прямо на экране дисплея. Компьютер определял координаты точек касания светового пера, а затем просчитывал геометрию кривой, прямой или геометрической фигуры и практически мгновенно выводил результат на экран.

Примеры работ, выполненных с помощью Sketchpad, из официального руководства к данной системе

Простая по сегодняшним меркам, программа Sketchpad требовала фантастических вычислительных мощностей того времени. Она запускалась на компьютере TX-2, который занимал несколько комнат исследовательской лаборатории имени Линкольна Массачусетского технологического института.

Лаборатория в Массачусетском технологическом институте

На видео ниже Сазерленд демонстрирует возможности нового человеко-машинного интерфейса.

Его система давала возможность творить невероятные для 1960-х годов вещи — по точкам рисовать линии и создавать на экране самые настоящие чертежи. А еще Sketchpad позволяла вносить изменения по ходу работы и масштабировать уже готовые элементы рисунка.

Одно из самых важных требований к Sketchpad, которое выдвигал Айвен, — точное выполнение инструкций оператора. Реализовать это было довольно сложно, так как пользователь мог «промахнуться» в нужной точке, да и само устройство ввода данных было несовершенным. Чтобы устранить эту проблему, в Sketchpad была использована система так называемых ограничителей. Эти ограничители позволяли абсолютно точно манипулировать деталями чертежа, например делать прямые параллельными или придавать двум отрезкам одинаковую длину. Для использования этих ограничителей применялся целый набор функциональных клавиш, который располагался рядом с экраном для ввода данных.

Схема манипулятора «световое перо», который использовался при работе со Sketchpad

А вот на этой презентации автор первого программного обеспечения для САПР уже показывает вполне рабочий вариант интерактивного интерфейса с несколькими окнами проекций и очень здраво рассуждает о потенциальных возможностях работы с 3D.

За разработку системы Sketchpad Айвен был награжден самой престижной премией в информатике, вручаемой Ассоциацией вычислительной техники, — премией Тьюринга.

Современные преподаватели могут многому поучиться у Сазерланда. Этот человек полностью отдал себя науке. Да что там себя — он в прямом смысле слова не пожалел для этой цели автомобиль. Вместе с своими студентами Айвен вручную сделал первый трехмерный цифровой скан Volkswagen Beetle. Да, именно вручную.

Задача была поставлена очень сложная. Тогда не было цифровых сканеров или цифровой фотографии, поэтому все приходилось делать «в лоб». Студенты как муравьи ползали по автомобилю и с помощью специальных мерных линеек рисовали на нем полигональную сетку, то, что сегодня специалисты по трехмерной графики называют wireframe, или каркас трехмерной модели. Перед началом работы с автомобиля были сняты некоторые детали — колеса, бампер и прочее, так как «оцифровывалась» одна основа — со всех сторон, сверху донизу. Оправдана ли была такая жертва? Конечно! Благодаря издевательствам над «жуком», Сазерленд разработал методику проецирования полигональных сеток на объект, благодаря чему и появилось современная 3D-графика.

Результат «ручной» оцифровки автомобиля

А еще Айвен сумел заинтересовать своей работой множество людей, которые продолжили развивать направление компьютерной 2D- и 3D-графики. И на фоне успеха все как-то забыли, что Volkswagen Beetle вообще-то принадлежал жене Айвена, да и ее реакция на поступок мужа осталась загадкой.

Визуализированный вариант автомобиля Сазерленда на основе полученного каркаса

А кем же были эти «муравьи»-студенты? Среди них было немало ярких личностей. Одного из тех, кто делал модель автомобиля, звали Джон Эдвард Уорнок (John Edward Warnock). Через десять лет после этой истории он станет соучредителем всем известной компании Adobe.

Другой молодой выпускник — Алан Кей (Alan Curtis Kay), тот самый, который изобрел концепт современных планшетных ПК под названием DynaBook (см. статью «Маленькие истории большого дизайна: от электробритв до планшетов»).

В создании этой модели также принимал участие младший научный сотрудник Буй Туонг Фонг (B˘i T˝ờng Phong). Сегодня модель Фонга используется во многих трехмерных движках.

Именно на модели первого трехмерного автомобиля Фонг протестировал свою знаменитую систему затенения, которая впоследствии получила его имя — Phong. В любом трехмерном редакторе, где имеется возможность настройки материалов, среди прочих вариантов можно выбрать алгоритм затенения по Фонгу. Метод Фонга основан на интерполяции нормалей поверхности по растрированным полигонам и позволяет вычислить цвет пикселей с учетом интерполированной нормали и модели отражения света.

Проект Сазерленда практически не имел аналогов. Единственная система, которая имела схожий принцип, — коммерческая разработка General Motors и IBM, которая называлась DAC-1 (Design Augmented by Computers). Эта консоль также управлялась при помощи светового пера, но была менее удобной и к тому же недешевой.

⇡#Одной левой: первая компьютерная анимация руки

Привычка гнаться за мощностями компьютерного железа привела к распространенному среди пользователей убеждению, будто без современной видеокарты невозможно получить 3D-изображение. Но это совсем не так. Представьте себе, что на третье измерение замахивались более полувека тому назад. Еще до того знаменательного момента, когда компьютер по-настоящему стал персональным, инженеры уже могли заниматься (и занимались) трехмерной анимацией. И приложил к этому руку будущий основатель и президент студии Pixar, а также глава Walt Disney Animation Studios и DisneyToon Studios Эдвин Кэтмелл (Edwin Catmull).

Причем сделал это в буквальном смысле слова — он оцифровал свою левую кисть руки и создал демонстрационную анимацию движений пальцев на ней.

Кэтмелл с детства интересовался процессом создания анимации. У него даже был собственный самодельный стенд, на котором Эдвин пытался делать первые примитивные мультфильмы. Однако, как и многие другие выпускники высших учебных заведений, он не сразу нашел свое призвание. Сразу после окончания университета Юты он сначала пошел работать в компанию Boeing, но уже через год экономический кризис заставил Боинг сократить тысячи сотрудников, и Эд оказался среди них. После этого недавний выпускник снова вернулся в университет, чтобы продолжить обучение в аспирантуре.

Айвен Эдвард Сазерленд, работавший в то время профессором в университете Юты, стал для Кэтмелла наставником и поддержал молодого аспиранта в стремлении изучать интерактивную компьютерную графику. Кэтмелл воспользовался тем же методом, что и Айвен для оцифровки своего автомобиля. Создание анимации трёхмерной руки проводилось в несколько этапов. По сравнению с масштабным проектом Айвена по оцифровке Volkswagen Beetle, Кэтмеллу было несколько проще — он просто разрисовал слепок своей левой руки, отметив на ней расположение ребер и узлов полигональной сетки. Далее в лаборатории эта сетка была считана специальным устройством, и по полученным данным была составлена трехмерная модель.

Процесс оцифровки руки Кэтмелла

Кэтмелл написал программу для анимации этой модели. Эта анимация была визуализирована и использована как хорошее дополнение к дипломному проекту. Поверхность руки деформировалась, пальцы сгибались и разгибались, а сама кисть поворачивалась на экране. Для большего эффекта Кэтмелл даже позволил «заглянуть» внутрь модели, продемонстрировав зрителю, что 3D-рука полая внутри.

Работа молодых ученых не пропала даром. Модель руки, вращающаяся в трехмерном пространстве, использовалась в фантастическом фильме Futureworld («Мир будущего») 1976 года. Он повествовал о курортном отеле, обслуживающий персонал которого состоит из роботов. Для имитации высоких технологий в ход пошло все — и отрендеренная анимация, и каркас трехмерной модели.

Помимо этой трехмерной руки, студентами была сделана еще более сложная работа — анимированная модель головы человека.

Ее подготовил друг и коллега Кэтмелла — Фред Парк (Fred Parke), который также принимал участие в оцифровке модели левой руки Эдварда.

Он даже попытался синхронизировать звук и движение губ компьютерной модели. И это в 1974 году!

Модель человека студенты между собой называли Болди, то есть «лысый». Ее каркас состоял из 900 треугольников.

В середине восьмидесятых лаборатория Доминика Массаро (Dominic Massaro) продолжила работу над этой моделью и уже на более продвинутой технике «оживила» голову, наделив ее большим набором речевой мимики. Сам же профессор Массаро слегка изменил имя на итальянский манер — Baldi и зарегистрировал как торговую марку. И уже не так давно под его началом был запущен выпуск приложения для iOS, в которых присутствует говорящая 3D-голова, сделанная еще в семидесятых годах.

⇡#Кошечка и уравнения: советская компьютерная анимация

Термин «компьютерная анимация» в середине прошлого века был чем-то уж очень экзотическим. Компьютеры, равно как и печатающие устройства, были только в распоряжении исследовательских организаций и, понятное дело, у военных. Ну, а в Советском Союзе про компьютерную анимацию люди и вовсе не слышали, за исключением небольшой группы энтузиастов, которые предполагали, что с помощью вычислительной техники вполне реально «нарисовать» анимацию. Один из таких людей — математик Николай Николаевич Константинов.

Этот человек — настоящая легенда отечественной математики. Константинов — один из самых талантливых и неординарных ученых, который сумел не только сделать огромный вклад в отечественную науку и систему образования, но и передать свои знания последующим поколениям. Среди его учеников очень много крупных математиков и учёных, не говоря уже про победителей математических соревнований и олимпиад.

В далеком 1968 году он создал первую компьютерную анимацию на полторы минуты. Объектом его внимания стала кошка, отсюда и название мини-мультфильма — «Кошечка».

Математик решил создать мультфильм, запрограммировав движения кошки и распечатав каждый кадр анимации с заново перерисованным силуэтом. Реализация подобной идеи могла возникнуть лишь у человека, который не только превосходно разбирается в высшей математике, но и видит ее практическое применение.

Поскольку мышцы животного, сокращаясь, управляют ускорением тех или иных частей тела, Константинов решил, что основой алгоритма движений животного вполне могут стать дифференциальные уравнения второго порядка. Графическая интерпретация силуэта кошки была достигнута с помощью символьного массива. Математик разбил контур кошки на параметрические «бруски», а затем с помощью гипотетических формул, описывающих походку животного, воссоздал простенький сценарий движений, который включал несколько шагов, поворот головы и замедление.

В этой работе ему помогали два студента МГУ — Владимир Пономаренко и Виктор Минахин. Николай Николаевич вспоминал потом о забавной детали этого проекта: для того, чтобы вывести правильную формулу движений кошки, Виктор пытался изображать кошку — становился на четвереньки и шагал по полу, стараясь понять, какие мышцы включаются в работу.

Хотя сам Константинов впоследствии и опровергал реалистичность достигнутого результата, ссылаясь на гипотетичность математических выкладок, однако трудно не заметить, насколько правдоподобно двигается в кадре животное.

На кафедре общих проблем управления механико-математического факультета Московского университета была подготовлена теоретическая часть этой задачи, а отладка самой программы по просчету дифференциальных уравнений и ее эксплуатация производилась в Вычислительном центре Московского государственного педагогического института. Компьютер, который использовался для просчетов этой анимации, носил гордое название БЭСМ-4 («Большая Электронно-Счетная Машина»).

БЭСМ-4 имела очень мало общего с тем, что мы сегодня называем компьютером. На всю страну было выпущено всего 30 таких устройств. Оперативная память в БЭСМ-4 была сделана на ферритных сердечниках (8192 слова, слова 45-разрядные, организованные в два куба по 4к слов). Производительность этого «шкафа» составляла до сорока тысяч операций в секунду. Принтер для большой электронно-счётной машины имел не менее ёмкое имя — алфавитно-цифровое печатающее устройство АЦПУ-128.

Если присмотреться к покадровой прорисовке, можно увидеть незначительные случайные нежелательные артефакты — по-своему это первые «глюки» компьютерной визуализации, то есть рендеринга.

Отдельные кадры анимации «Кошечка»

Что касается рожицы, которую кошка строит в начале короткометражки — это работа не математика, а художника-весельчака, который делал анимацию еще для незабываемого советского фильма «Веселые ребята». Его тоже пригласили для работы над этим проектом.

Интересно, что в то время Константинов не был единственным человеком в СССР, кто использовал метод компьютерной анимации. Однако другие попытки визуализации на компьютере, такие как, например, анимация процессов внутри молекулы ДНК, были скучны и малопонятны неподготовленному зрителю.

⇡#Заключение

Сейчас компьютер — это универсальный инструмент. Он может использоваться и для рисования, и для создания анимации, и для подготовки видео. Единственное, чего ему не хватает, — творческого начала. Впрочем, возможно, и это дело времени.

Появление компьютерной техники и развитие компьютерной графики в каком-то смысле позволило человеку по-новому взглянуть на мир. Многое из того, что раньше было недоступным для человеческого зрения, то, что было слишком быстрым или слишком медленным, очень маленьким или чересчур большим, — в компьютерной модели стало очевидным и понятным. Медицина, техника, инженерия, космос — компьютерная графика используется в любой сфере деятельности человека. То, что начиналось как обычная световая точка на экране, один пиксель, отображение минимальной компьютерной информации, постепенно трансформировалось в линию, двигающийся образ на экране, а затем в виртуальную и дополненную реальность. И предел этой эволюции пикселя находится где-то далеко за гранью человеческого понимания. И скорее всего, самое интересное еще впереди.

Если Вы заметили ошибку — выделите ее мышью и нажмите CTRL+ENTER.

Платоновых тел — EnchantedLearning.com

Платоновы тела — EnchantedLearning.com

Рекламное объявление.

EnchantedLearning.com — это сайт, поддерживаемый пользователями.
В качестве бонуса участники сайта получают доступ к версии сайта без баннерной рекламы и удобным для печати страницам.
Щелкните здесь, чтобы узнать больше.

(Уже зарегистрированы? Нажмите здесь.)

Есть только пять геометрических тел, которые можно создать, используя правильный многоугольник, и у которых одинаковое количество этих многоугольников пересекаются в каждом углу.Пять Платоновых тел (или правильных многогранников) — это тетраэдр, куб, октаэдр, додекаэдр и икосаэдр.
История платоновых тел

Пять правильных многогранников были открыты древними греками. Пифагорейцы знали о тетраэдре, кубе и додекаэдре; математик Теэтет добавил октаэдр и икосаэдр.
Эти формы также называются Платоновыми телами в честь древнегреческого философа Платона; Платон, который очень уважал работы Теэтета, предполагал, что эти пять твердых тел являются формами основных компонентов физической вселенной.

Платоновы тела — Информация
Примечание: формула Эйлера гласит, что (Число граней) + (Число вершин) — (Число ребер) = 2.
Рабочие листы и задания для печати

ТЕТРАЭДРОН

Сделайте бумажный тетраэдр, пирамиду, образованную четырьмя треугольниками.

ТЕТРАЭДРОН ИЗ МАЛЕНЬКОЙ КОНВЕРТЫ
Это невероятно простой способ сделать тетраэдр (пирамиду) из маленькой конверта.

КУБ

Создайте бумажный куб, твердую геометрическую фигуру с шестью квадратными гранями.

OCTAHEDRON

Сделайте октаэдр из бумаги. Октаэдр — это восьмиугольное правильное геометрическое тело.

DODECAHEDRON

Сделайте бумажный додекаэдр. Додекаэдр — это двенадцатигранное правильное геометрическое тело, состоящее из пятиугольников.

ICOSAHEDRON

Сделайте бумажный икосаэдр. Икосаэдр — это правильное геометрическое тело с двадцатью сторонами, состоящее из равносторонних треугольников.

Сопоставьте каждый правильный многогранник с его именем и его развернутой формой

Проведите линии между каждым Платоновым телом (правильным многогранником), его именем и развернутой формой. Многогранники: тетраэдр, куб, октаэдр, додекаэдр, икосаэдр. Или перейдите к ответам.

Раскладывание трехмерных фигур: сети куба и тетраэдра

Нарисуйте развернутый куб и тетраэдр. Или перейдите к ответам.

Многогранники: заполнение пробелов

Заполните имя, количество граней, сетку, количество вершин, количество ребер и форму граней для пяти многогранников (тетраэдр, куб, октаэдр, додекаэдр). , и икосаэдр).Или перейдите к ответам.

Enchanted Learning ^®
Более 35 000 веб-страниц
Примеры страниц для потенциальных подписчиков или щелкните ниже

Нажмите, чтобы прочитать нашу Политику конфиденциальности

Зачарованный поиск обучения

Найдите на веб-сайте Enchanted Learning:

Рекламное объявление.

Что такое трехмерные формы?

Трехмерные игры

Объем с использованием юнит-кубов

Единичный куб — это куб, объем или емкость которого составляет 1 юнит. Вы можете подсчитать количество единичных кубиков, которые могут поместиться в твердое тело, чтобы определить его объем.

охватывает Common Core Curriculum 5.MD.5.aИграть сейчасПосмотреть все игры по геометрии >>

Учитесь с помощью полной программы обучения математике K-5

Что такое трехмерные формы?

В геометрии трехмерную фигуру можно определить как твердую фигуру или объект или форму, имеющую три измерения — длину, ширину и высоту.В отличие от двухмерных форм, трехмерные формы имеют толщину или глубину.

allowfullscreen webkitallowfullscreen allow = «autoplay; encrypted-media»

Учитесь с помощью полной программы обучения математике K-5

Атрибуты трехмерной фигуры — это грани, ребра и вершины. Три измерения составляют края трехмерной геометрической формы.

Куб, прямоугольная призма, сфера, конус и цилиндр — это основные трехмерные формы, которые мы видим вокруг себя.

Мы видим кубик в кубике Рубика и игральную кость, прямоугольную призму в книге и коробке, сферу в глобусе и шар, конус в моркови и рожок мороженого и цилиндр в ведре и бочка, вокруг нас.

Вот список трехмерных или трехмерных фигур с их названиями, изображениями и атрибутами.

Название 3D-формы :	Изображение 3D формы :	Атрибуты :
Куб		Лица — 6 Кромки — 12 вершин — 8
Прямоугольная призма или кубоид		Лица — 6 Кромки — 12 вершин — 8
Сфера		Изогнутая грань — 1 Кромки — 0 вершин — 0
Конус		Плоское лицо — 1 Изогнутая грань — 1 Кромки — 1 вершин — 1
Цилиндр		Плоское лицо — 2 Изогнутая грань — 1 Кромки — 2 вершин — 0

Интересные факты

Все трехмерные формы состоят из двухмерных форм.

Давайте споем!

3D-фигуры толстые, а не плоские.

Найди конус в шапке на день рождения!

Вы видите сферу в баскетбольном мяче,

И кубоид в таком высоком здании!

Вы видите куб в кости, которую вы бросаете,

И цилиндр в сияющем флагштоке!

Давай сделаем это!

Вместо того, чтобы показывать видео о трехмерных фигурах вашим детям и воспитанникам детского сада, попросите их наблюдать и выделять предметы вокруг них, в которых они могут найти трехмерные формы.

Вы можете также попросить их определить и отсортировать трехмерную форму и ее атрибуты.

Сопутствующий математический словарь

Геометрия

Геометрия — это всего фигур, и их свойства.

Если вам нравится играть с объектами или рисовать, то геометрия для вас!

Геометрию можно разделить на:

Плоская геометрия — это плоские формы, такие как линии, круги и треугольники… фигуры, которые можно нарисовать на листе бумаги

Solid Geometry — это трехмерные объекты, такие как кубы, призмы, цилиндры и сферы.

Подсказка: попробуйте нарисовать некоторые формы и углы по мере изучения … это поможет.

Точка, линия, плоскость и твердое тело

Точка не имеет размеров, только позиция

Линия одномерная

Самолет двумерный (2D)

Твердое тело трехмерное (3D)

Почему?

Почему мы делаем геометрию? Чтобы открывать закономерности, находить площади, объемы, длины и углы, а также лучше понимать мир вокруг нас.

Плоская геометрия

Плоская геометрия — это все о формах на плоской поверхности (например, на бесконечном листе бумаги).

Полигоны

Многоугольник — это двумерная фигура, состоящая из прямых линий. Треугольники и прямоугольники — это многоугольники.

Вот еще несколько:

Круг

Теоремы о круге (расширенная тема)

Символы

В геометрии используется много специальных символов.Вот вам краткая справка:

Геометрические символы

Конгруэнтные и похожие

Уголки

Типы углов

Преобразования и симметрия

Преобразований:

Симметрия:

Координаты

Более сложные темы по геометрии плоскости

Пифагор

Конические секции

Теоремы о круге

Центры треугольника

Тригонометрия

Тригонометрия — отдельная тема, поэтому вы можете посетить:

Твердая геометрия

Solid Geometry — это геометрия трехмерного пространства, в котором мы живем…

… начнем с самых простых форм:

Общие 3D-формы

Многогранники и неполигранники

Есть два основных типа твердых тел: «Многогранники» и «Неполиэдры»:

Многогранники (должны иметь плоские грани) :

Non-Polyhedra (когда любая поверхность
не плоский) :

Что такое твердые геометрические формы или тела?

Вы наверняка знаете о плоских геометрических фигурах, поэтому сегодня мы поговорим о твердых геометрических фигурах , которые также известны как геометрические фигуры или тела .

Эти фигуры имеют три измерения — длину, глубину и высоту. Другими словами, эти фигуры имеют объем и можно сказать, что они занимают место в космосе.

Основные типы твердых геометрических фигур

Многогранники

Слово «многогранник» происходит от греческого слова «поли», что означает много и от «эдрон», что означает основание или сиденье . Мы говорим о геометрических фигурах, которые имеют несколько граней и являются плоскими.Среди них у нас:

Правильные многогранники: они известны как платоновы тела и характеризуются наличием равных граней. Их пять: тетраэдр, шестигранник (куб), октаэдр, додекаэдр и икосаэдр.

Призмы: состоят из двух многоугольных оснований одинакового размера и формы, а их боковые грани представляют собой параллелограммы.
Пирамиды: состоят из многоугольной грани, которая является его основанием, и боковых граней в форме треугольников.

В реальной жизни мы можем найти очень много объектов в форме многогранников, таких как кубик льда, пирамида или пакет молока.

Характеристики многогранников:

Грань : грани многогранника — это плоские поверхности снаружи многогранника.
Край: ребра многогранников состоят из сторон, образующих каждую грань.
Вершины: вершины многогранника — это точки пересечения его ребер.Три грани встречаются в одной вершине.

Круглые тела

Есть несколько твердых геометрических фигур, полностью состоящих из изогнутых и плоских поверхностей. Среди них самые распространенные круглые тела, которые мы можем найти:

Конус: круглый корпус, состоящий из круглого основания и изогнутой поверхности.

Сфера: полностью искривленное геометрическое тело, состоящее из искривленной поверхности.

Цилиндр: геометрическое тело, состоящее из изогнутой поверхности и двух плоских круглых оснований.

Мы можем найти множество круглых тел в реальных объектах, таких как вулкан (конус), бильярдный шар (сфера) или ведро с краской (цилиндр). Если вы хотите продолжать изучать геометрические фигуры и другие темы первичной математики, зарегистрируйтесь в Smartick и попробуйте бесплатно!

Подробнее:

Команда по созданию контента.
Многопрофильная и многонациональная команда, состоящая из математиков, учителей, профессоров и других специалистов в области образования!
Они стремятся создавать максимально качественный математический контент.

Складывание для придания формы — SAS

Основное внимание в этом уроке уделяется выявлению и описанию двухмерных форм. Студенты получают возможность просмотреть знакомые формы в начале урока. Затем они находят эти формы в окружающей среде, используя средства поиска геометрических фигур. После определения известных форм в новой обстановке они создают незнакомые формы, складывая бумагу. Это предназначено для того, чтобы помочь учащимся понять, что существует множество видов фигур, и их можно описать в соответствии с их атрибутами.Затем учащиеся размышляют над своим пониманием фигур, сортируя фигуры и обсуждая их общие атрибуты.

«Сегодня мы продолжим работу по геометрии. Мы обсудим несколько слов из словарного запаса геометрии. Во время нашего раздела мы продолжим добавлять к нашим концепциям геометрии стену . Мы поговорим о формах, которые мы находим в классе. Затем мы создадим новые формы, сложив бумагу, и отсортируем их по атрибутам. В мире вокруг нас множество форм.Вы уже узнали о некоторых формах. Давайте составим список фигур на этой диаграмме «.

Запишите ответы учащихся на листе бумаги. Просматривайте словарные слова, такие как сторона и вершина , когда учащиеся рассказывают о них, и напомните им, что мы описываем формы по их атрибутам. (Вы могли бы сказать, например, «У квадрата четыре стороны и четыре вершины или угла».)

Поиск геометрической формы

«Формы повсюду.Следующие несколько минут вы будете искать фигуры в нашем классе. Я собираюсь дать каждому из вас поисковик геометрической формы » (M-2-5-1_Geometry Shape Finders.doc). Поднимите искатели формы и просмотрите форму на каждом из них. «Вы должны найти только те формы, которые соответствуют вашему искателю геометрических фигур, и записать их в свой математический журнал. Например, мой искатель геометрической формы имеет кружок вверху. Я просмотрю его, чтобы найти в комнате что-нибудь, имеющее форму круга.”

Поднесите искатель геометрической формы к глазу и смотрите сквозь него — как через увеличительное стекло.

«Ой, смотрите! Я вижу пенни. Он имеет ту же форму, что и мой искатель геометрической формы. Мне нужно будет записать это в свой математический дневник ».

Раздайте искатели геометрических форм и дайте ученикам возможность искать формы в течение 5–7 минут. Студенты должны записывать свои результаты в свои математические журналы. Снова соберите класс и обсудите формы, найденные в вашем классе.Поощряйте учащихся описывать формы и их атрибуты, используя соответствующий словарный запас. Попросите учащихся обменять искатели форм и поискать новую форму, повторив упражнение, чтобы каждый учащийся имел возможность найти несколько видов фигур.

Складывание бумаги для создания новых форм

Для этого задания вам понадобятся два квадратных листа бумаги размером 8 дюймов, по одному квадратному листу размером 8 дюймов для каждого учащегося и по одному листу бумаги для рисования размером 12 на 18 дюймов для каждого учащегося.

Скажем, «Давайте взглянем на несколько разных форм. Когда мы смотрим на каждую фигуру, давайте найдем количество сторон и количество вершин, которые у нее есть. Начнем с моего квадрата.

Покажите ученикам один из 8-дюймовых квадратов. «Сколько сторон у этого квадрата?» ( 4 ) « Сколько вершин или углов у этого квадрата?» ( 4 ) По мере того, как учащиеся будут давать ответы, запишите информацию на доске или на листе бумаги, как показано ниже.

Форма	Имя	Стороны	Вершины
	Площадь	4	4

Попросите учащихся скопировать диаграмму в свой математический журнал, оставив место для добавления дополнительных строк позже. «Теперь я буду складывать бумагу несколько раз. Внимательно смотри, как я складываю бумагу. Когда я закончу, каждый из вас получит квадратный лист бумаги, и я дам вам пошаговые инструкции, как его сложить. Прямо сейчас смотри, как я складываю свой квадрат ».

Возьмите квадратный лист бумаги диаметром 8 дюймов, чтобы весь класс мог видеть процесс складывания.

Чтобы сложить бумагу, выполните следующие действия. Наглядные инструкции представлены в примере складывающегося квадрата (M-2-5-1_Пример складывающегося квадрата.док). Когда вы сбрасываете карты, объясните студентам, что вы делаете.

Сложите квадрат пополам по вертикальной линии симметрии. Обязательно сделайте хорошую складку.
Откройте квадрат.
Сложите квадрат пополам по горизонтальной линии симметрии. Обязательно сделайте хорошую складку.
Откройте квадрат.
Приведите каждую угловую вершину к пересечению обеих линий симметрии. Хорошо загните и загните.
Повторите шаг 5 для каждой угловой вершины.
Откройте квадрат так, чтобы вы могли видеть все складки.

«После того, как вы сложите бумагу, чтобы сделать складки, вам нужно будет сложить квадрат на созданных вами складках, чтобы получить новые формы. Например, если я возьму свой квадрат и сложу его пополам, я получу форму. Какая у меня форма? » ( прямоугольник ) «Да, я сформировал прямоугольник. Помните, что квадрат — это тоже прямоугольник. Теперь я запишу эту фигуру в нашу таблицу ». Обведите прямоугольник на графике.Напишите «Прямоугольник» во втором столбце. «Давайте прибавим к нашей диаграмме количество сторон и количество вершин. Сколько сторон у прямоугольника? » ( 4 ) «Сколько у него вершин?» ( 4 ) Добавьте эту информацию в диаграмму. По мере того, как вы записываете информацию на доске, студенты будут заполнять свои собственные таблицы в своих математических журналах.

Форма	Имя	Стороны	Вершины
	Площадь	4	4
	Прямоугольник	4	4

Ученики должны заметить, что и квадрат, и прямоугольник имеют 4 стороны, 4 вершины и 4 прямых угла.Скажем, «И квадрат, и прямоугольник являются частью большей группы многоугольников, называемых четырехугольниками. У всех четырехугольников 4 стороны, 4 вершины и 4 угла ».

Раздайте каждому ученику квадрат размером 8 дюймов и лист бумаги для рисования размером 12 на 18 дюймов. «Теперь вам пора сделать фолд. Начнем со складывания и складывания складок. Вот шаги ».

Проведите учеников по процессу складывания. Используйте второй кусок квадратной бумаги диаметром 8 дюймов для моделирования каждого шага.Это может занять несколько минут. Когда ученики развернут свой квадрат, он будет иметь следующие складки.

После того, как все сложили квадрат, дайте студентам время изучить различные формы, которые они могут сделать, сложив квадрат один или несколько раз. Напомните учащимся, что для создания фигур используйте только те складки, которые они уже сделали; они не должны образовывать новых складок. Попросите учащихся нарисовать новые формы на бумаге для рисования.Они должны назвать каждую форму и указать количество сторон и вершин, которые у нее есть. Вот различных форм, которые они могут сделать:

Категории форм

Пока учащиеся создают фигуры и обводят их на бумаге, разложите по комнате несколько листов диаграммной бумаги. Пометьте диаграмму определенными атрибутами или категориями, такими как «Фигуры с четырьмя сторонами» или «Фигуры с более чем четырьмя вершинами».»Просматривая работы учащихся, выберите нескольких учащихся, чтобы обвести их формы на классной диаграмме в нужной категории.

Обсудите с классом формы в каждой категории. Это хорошая возможность познакомить студентов с новым словарным запасом, таким как четырехугольник , пятиугольник и атрибут .

Пока ученики обводят свои формы, обсудите, какие формы «одинаковые» и что это означает. Введите термин «конгруэнтный», означающий, что одна фигура будет соответствовать другой, если поместить ее поверх нее.Будет несколько возможностей показать (или попросить студентов показать вам) конгруэнтные формы:

Это обсуждение также принесет некоторую неформальную лексику преобразований. Возможно, вам придется объяснить: «Это то же самое, за исключением того, что перевернули на , а перевернули на ».

У вас будет возможность оценивать учащихся с помощью обсуждений и вопросов, пока учащиеся исследуют новые формы в процессе складывания.Вы можете разделить учащихся на небольшие группы, чтобы уточнить их понимание или оценить их обучение.

Примеры вопросов:

«Какую форму вы получили, сложив квадрат один раз? Два раза?»
«Вы создавали конгруэнтные формы? Откуда вы знаете?»
«Я вижу, у вас похожие формы. Вы можете сказать мне, почему эти две формы похожи? »
«Что для вас сложного в этой проблеме?»
«Интересно, сможем ли мы создать фигуру, у которой меньше четырех сторон.”
«Интересно, какая форма будет иметь больше всего вершин».

Убедитесь, что учащиеся записывают информацию о фигурах на своей бумаге. Когда учащиеся делятся ответами, некоторые могут сказать, что у них появилась новая форма, хотя на самом деле это поворот или переворот уже упомянутой формы. Обязательно укажите на это ученикам, накладывая фигуры друг на друга.

Добавочный номер :

Используйте перечисленные ниже мероприятия и стратегии, чтобы удовлетворить потребности ваших учеников в течение года.

Процедура: Используйте входной билет (M-2-5-1_Entrance Ticket Lesson 1 и KEY.doc), чтобы оценить знания учащихся о формах. Входной билет можно использовать для закрепления навыков, полученных на предыдущем уроке, и он может быть полезным инструментом предварительной оценки.
Расширение: Готовые учащиеся могут использовать карты сортировки форм и формирования рисунков (M-2-5-1_ Карты сортировки и формирования рисунков по фигуре.doc), чтобы попрактиковаться в сортировке фигур в соответствии с их атрибутами. Студенты должны создать категории, а затем отсортировать карточки по соответствующим категориям.
Малые группы: Некоторым учащимся может быть трудно складывать бумаги. При необходимости приготовьте заранее сложенные 8-дюймовые квадраты. Проведите студентов, которым нужно больше практики, через серию складок в небольшой группе. Уменьшите количество необходимых складок. Затем помогите им записать количество сторон и вершин для каждой формы.
What’s My Rule ?: В качестве быстрого перехода или разминки учащиеся могут сыграть в What’s My Rule ?. Предложите одному ученику разделить группу фигур на две или более групп.Класс рассмотрит группы и угадает, какой атрибут учащийся использовал для сортировки.

Понимание трехмерной геометрии | Универсальный класс

Понимание трехмерной геометрии

Глядя на параллельность и перпендикулярность в трех измерениях, мы видим, что применимы многие из тех же принципов, но при этом добавляются некоторые сложности.

Ключевые термины

o Косые линии

o Оси

o Поперечное сечение

Цели

o Распознавать перпендикулярные, параллельные и наклонные линии в трех измерениях

o Уметь изображать простые трехмерные фигуры с помощью двухмерных чертежей

o Знать, что такое поперечное сечение и как его можно использовать для соотнесения двух- и трехмерной геометрии

Объекты в реальной жизни имеют три пространственных измерения, поэтому нам полезно понять некоторые фундаментальные аспекты трехмерной геометрии.Во многих отношениях трехмерная геометрия — это просто расширение двухмерной геометрии; применимы многие из тех же принципов. В этой статье мы рассматриваем параллельность и перпендикулярность в трех измерениях, а затем рассмотрим рисование трехмерных фигур на двухмерной поверхности. Наконец, мы кратко рассмотрим поперечные сечения.

Параллельность и перпендикулярность в трех измерениях

В двух измерениях мы отметили, что любые две прямые, которые не пересекаются, параллельны.Напомним, однако, что мы дали немного более фундаментальное определение, которое включало соотношение углов, образованных трансверсалью, пересекающей параллельные линии. Теперь представьте две линии в трех измерениях. В трех измерениях вы, вероятно, легко можете представить две линии, которые на самом деле не параллельны, но также не пересекаются. Пример показан ниже с использованием линий l и m , где одна из линий ( l ) показана «на конце» (то есть выходит на поверхность страницы и выходит за ее пределы), так что она появляется как точка.

Обратите внимание, что две линии не имеют точки пересечения, и тем не менее, они не являются тем, что мы бы считали «параллельными». Это то, что мы называем косыми линиями. Отметьте также, что эти линии, хотя они в некотором смысле выглядят как «перпендикулярные», на самом деле таковыми не являются, потому что они не пересекаются. Однако, если бы они пересекались, то они действительно были бы перпендикулярны, как показано ниже.

В двумерной (плоской) геометрии для данной точки на прямой существует только одна перпендикулярная линия, как показано ниже.

В трехмерной геометрии существует бесконечное количество линий, перпендикулярных данной линии. Рассмотрим линию l , которая пересекает плоскость под прямым углом (другими словами, везде, где измеряется угол вокруг линии относительно плоскости, он всегда равен 90 °). Мы можем провести на плоскости бесчисленное количество линий, пересекающих линию l ; поскольку они лежат в плоскости, они пересекают l под прямым углом.

Аналогично, в плоской геометрии существуют только две линии, параллельные данной линии на некотором фиксированном расстоянии d , как показано ниже.

В трехмерной геометрии, опять же, существует бесконечное количество линий, параллельных данной линии на некотором фиксированном расстоянии d . Представьте себе линию l , проходящую под прямым углом через плоскость еще раз, как показано выше. Но на этот раз нарисуем на плоскости окружность радиусом d .

Теперь мы можем нарисовать любое количество линий, пересекающих окружность и плоскость под прямым углом — эти линии также параллельны l .

Мы можем определить параллельность и перпендикулярность для плоскостей в трех измерениях аналогично тому, как мы определили их для линий в двух измерениях. Любые две пересекающиеся плоскости (которые не являются одной и той же плоскостью) образуют линию пересечения; это трехмерный аналог точки пересечения двух прямых.Такое пересечение двух плоскостей показано ниже.

Если две плоскости не пересекаются, то они параллельны. Если угол пересечения равен 90 °, то плоскости перпендикулярны. Этот угол пересечения измеряется при взгляде на плоскости «на краю», так что линия пересечения перпендикулярна поверхности этой страницы, как показано ниже. (Обратите внимание, что если смотреть на плоскости с этой точки зрения, они кажутся линиями, а линия пересечения — точкой.)

Таким образом, мы можем видеть, что параллельность и перпендикулярность в трех измерениях, хотя они имеют сходство с одними и теми же концепциями в двух измерениях, принимают несколько более сложный характер. Тем не менее, расширяя то, что мы уже узнали в двух измерениях, мы можем понять геометрические концепции также и в трех измерениях.

Можно задаться вопросом, можно ли расширить геометрию до четырех или более измерений. Ответ — да, но такая попытка становится намного труднее, потому что у нас нет реального опыта, который помог бы нам представить геометрическое пространство с более чем тремя измерениями.Например, хотя мы легко понимаем концепции «вверх-вниз», «влево-вправо» и «вперед-назад» (три пространственных измерения), нам очень трудно представить себе четвертое измерение. Как бы выглядело такое измерение (или направление)? Такие многомерные геометрии действительно играют важную роль в определенных областях исследования, но они не так применимы в повседневной жизни, как двух- и трехмерная геометрия.

Практическая задача : Покажите, что две линии, которые пересекаются поперечным сечением, тем самым образуя соответствующие совпадающие углы, не обязательно параллельны в трехмерной геометрии.

Решение : Эта проблема требует от нас критического мышления в отношении линий и плоскостей в трех измерениях. Во-первых, давайте начнем с двух линий, которые мы будем считать параллельными, и разрежем эти линии перпендикулярно, как показано ниже.

Теперь рассмотрим поперечную линию n . Мы знаем, что в трех измерениях существует бесконечное количество линий, перпендикулярных n для данной точки пересечения; все эти перпендикулярные линии лежат на одной плоскости.Нарисуем плоскость для точек, в которых параллельные прямые l и m пересекаются n .

Но что, если мы «повернем» либо линию l , либо m в соответствующей плоскости перпендикулярности? Во-первых, мы знаем, что линии l и m больше не будут перпендикулярными; они превратятся в кривые линии. Кроме того, мы знаем, что углы, образованные пересечением l и n (а также m и n ), останутся такими же, поскольку эти пары селезенок все равно будут перпендикулярными, как показано ниже.

Таким образом, даже несмотря на то, что соответствующие углы для линий l и m , пересеченных поперечно n , совпадают (все они равны 90 °), линии не обязательно параллельны .

Трехмерный чертеж

Очевидно, что трудно нарисовать фигуру в трех измерениях, когда используется двухмерный лист бумаги (или экран компьютера). Тем не менее, мы можем очень легко сделать чертежи, которые выглядят трехмерными, следуя нескольким простым правилам.Сначала определите направления (лучи) для каждого измерения. Хотя в этом нет необходимости, иногда полезно нарисовать набор из осей , например, показанный ниже.

Обратите внимание, что мы показали, что все оси взаимно перпендикулярны — точно так же, как направления влево-вправо, вверх-вниз и назад-вперед перпендикулярны. Чтобы нарисовать фигуру, имеющую трехмерный вид, используйте расстояния, параллельные определенной оси, чтобы создать иллюзию того, что фигура вытянута в этом направлении.Обратите внимание, например, на то, как куб показывает трехмерный характер в силу его взаимосвязи с осями (даже если вы игнорируете оси, достигается тот же эффект).

Практическая задача : Используйте набор осей, чтобы нарисовать треугольник, который кажется «наклоненным» в трех измерениях. (Другими словами, плоскость, образованная треугольником, не параллельна поверхности этой страницы.)

Решение : Начните с рисования набора осей, как мы делали ранее.

Теперь давайте выберем три точки для треугольника и разместим по одной в какой-то точке на каждой оси. Это создаст эффект треугольника, имеющего протяженность в трех разных направлениях (измерениях). Наконец, соедините точки, как показано ниже.

Таким образом, мы создали треугольник, который кажется «наклоненным» в трех измерениях. Конечно, треугольник — это просто двухмерный рисунок, но с помощью осей мы можем создать иллюзию (хотя и несколько упрощенно) того, что треугольник «наклонен» относительно поверхности страницы.

Поперечные сечения

Рассмотрим какую-нибудь трехмерную фигуру, например, цилиндр; Затем представьте себе плоскость, которая пересекает эту фигуру, как показано в примере ниже. Пересечение плоскости и трехмерной фигуры называется поперечным сечением , , и это двухмерный «срез» (бесконечно малой ширины) фигуры.

В приведенном выше примере плоскость поперечного сечения перпендикулярна вертикальной ориентации цилиндра — таким образом, поперечное сечение представляет собой круг.Однако, если использовать другой угол, мы получим овал вместо круга для поперечного сечения.

Таким образом, мы можем видеть, что двумерная геометрия в некотором смысле может рассматриваться как «поперечное сечение» трехмерной геометрии.

Практическая задача : Какие двумерные фигуры образуются при взятии поперечного сечения сферы (например, ракетный мяч является примером сферы)?

Решение : Напомним, что поперечное сечение — это просто плоский «разрез» фигуры.Итак, нарисуем плоскость и сферу.

Теперь поперечное сечение формируется путем опускания сферы (в данном случае) на плоскость, точно так же, как мы могли бы опустить ее в бассейн с водой. Поскольку сфера идеально симметрична, результирующее сечение всегда представляет собой круг. В зависимости от того, где берется поперечное сечение относительно центра сферы, окружность может иметь радиус от нуля (плоскость касается касательной к сфере или просто касается ее в точке на поверхности сферы) к радиусу сферы.

Трехмерное рисование и геометрические эксперименты с трехмерной геометрией

«Я бы не рисовал так, как пишу, если бы не пошел в архитектурную школу. Там я научился абстрактно мыслить и рисовать, как архитектор ».

—Кармен Эррера

Беседа с Даной Миллер, 10 октября 2014 года.

Чтобы развить свой жесткий стиль абстракции, Кармен Эррера предприняла дисциплинированное, но очень изощренное исследование цвета и формы. Эррера изучала архитектуру всего один академический год, но этот опыт оказал на нее огромное влияние.Основные принципы рисования, которым она научилась на вводных курсах в Университете Гаваны, позволили ей представить трехмерную форму и преобразовать ее в двухмерное изображение на бумаге или холсте.

Вдохновленная советом своего коллеги-художника и друга Барнетта Ньюмана «не создавать что-то, а затем думать об этом, а думать о чем-то, а затем делать это», Кармен Эррера часто тратит недели на предварительные рисунки, пробуя разные формы и композиции и выполнение точных математических расчетов перед тем, как приступить к рисованию.Подготовительные рисунки, которые она делает для каждой картины, показывают, как Эррера часто мыслит в трехмерных терминах, а затем преобразует это изображение в двухмерное.

а. Распечатайте шаблон ромбовидной формы из руководства для учителя. Дайте каждому ученику по три ромбовидных фигуры. Попросите учащихся вырезать ромбы и поэкспериментировать с ними, чтобы сделать трехмерный куб. Предложите им выбрать три разных цвета для каждой формы ромба. Когда ученики закончат раскрашивать свои ромбы, попросите их скотчем или склейте кубики и повесьте их на стену, чтобы они образовали одно большое изображение.Как их большое изображение влияет на классную комнату?

г. Этот проект рекомендуется для старшеклассников. Изометрические формы визуально представляют трехмерные объекты в двух измерениях на архитектурных, технических и инженерных чертежах. Например, в кубе три оси координат выглядят одинаково укороченными, а угол между любыми двумя из них составляет 120 градусов. Чертеж может выглядеть искаженным, потому что масштаб объектов, которые появляются дальше, такой же, как объекты, которые кажутся ближе.Изометрическая сетка состоит из вертикальных и диагональных линий под углом 120 градусов, которые можно использовать в качестве шаблона для рисования трехмерных объектов. Распечатайте изометрическую сетку в руководстве для учителя и попросите своих учеников нарисовать простой геометрический объект, например мобильный телефон, другое электронное устройство или открытую книгу.