Как сделать многогранник из бумаги схема: куба, конуса, схемы и шаблоны для вырезания цилиндра, пирамиды, треугольника ✅ igrad.su

by alexxlab Posted in Разное on 02.06.202014.08.2020

Содержание

Как сделать из бумаги многогранник. Многогранники из бумаги

Бумажные поделки – это не только различные открытки и аппликации, выполненные в виде плоских изделий. Очень оригинальными получаются объемные модели фигур (фото 1). Например, можно сконструировать из бумаги многогранник. Рассмотрим некоторые способы его выполнения, используя схемы и фотографии.

История фигур

Древняя математическая наука уходит своими корнями в далекое прошлое, во времена процветания Древнего Рима и Греции. Тогда было принято связывать технические аспекты с философскими. Поэтому, согласно учению Платона (один из древнегреческих мыслителей), каждый из многогранников, состоящих из определенного количества одинаковых плоскостей, символизирует одну стихию. Фигуры из треугольников — октаэдр, икосаэдр и тетраэдр — ассоциируются с воздухом, водой и огнем соответственно и могут преобразовываться друг в друга благодаря однотипности граней, каждая из которых имеет три вершины. Землю же символизирует гексаэдр из квадратов. А додекаэдр, благодаря особенным пятиугольным граням, выполняет декоративную роль и является прототипом гармонии и мира.

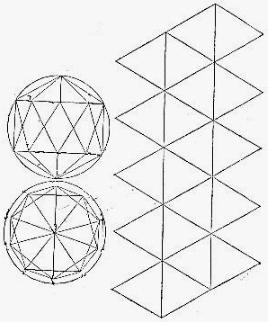
Также известно, что один из греческих математиков, Евклид, доказал в своем учении «Начала» неповторимость упомянутых платоновых тел и их свойство «вписываться» в сферу (фото 2). Сделан показанный из бумаги многогранник путем сворачивания сомкнутых между собой двадцати равнобедренных треугольников. Схема наглядно демонстрирует выкройку для изготовления фигуры. Рассмотрим подробнее все этапы работы по созданию икосаэдра.

Делаем двадцатигранник

Икосаэдр состоит из одинаковых по размеру равнобедренных треугольников. Его можно легко сложить, используя представленную на рисунке 2 развертку. Возьмите прямоугольный лист бумаги. Начертите на нем двадцать одинаковых по размеру и форме треугольников, расположив их в четырех рядах. При этом каждая грань одного будет одновременно являться стороной другого. Полученный шаблон используйте для изготовления заготовки. Она будет отличаться от основы-развертки наличием припусков для склеивания по всем внешним линиям. Вырезав из бумаги заготовку, согните ее по линиям. Формируя из бумаги многогранник, замыкайте крайние ряды между собой. При этом вершины треугольников соединятся в одну точку.

Правильные многогранники

Все фигуры отличаются друг от друга различным количеством граней и их формой. Кроме этого, некоторые модели могут быть сложены из цельного листа (как описано в примере изготовления икосаэдра), другие – только путем сбора из нескольких модулей. Классическими считаются правильные многогранники. Из бумаги их делают, придерживаясь главного правила симметрии – наличия в шаблоне полностью одинаковых граней. Существует пять основных видов таких фигур. В таблице приведены сведения об их названиях, количестве и формах граней:

Название	Кол-во граней	Форма каждой грани
тетраэдр	4	треугольник
гексаэдр	6	квадрат
октаэдр	8	треугольник
додекаэдр	12	пятиугольник
икосаэдр	20	треугольник

Разнообразие фигур

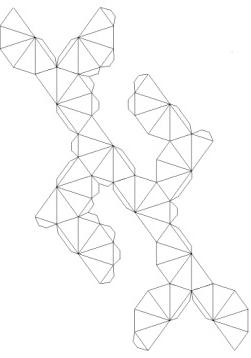
На основе пяти приведенных видов, используя умение и фантазию, умельцы легко конструируют множество различных моделей из бумаги. Многогранник может совершенно отличаться от вышеописанных пяти фигур, формируясь одновременно из различных по форме граней, например из квадратов и треугольников. Так получаются архимедовы тела. А если одну или несколько граней пропустить, то получится открытая фигура, просматриваемая как снаружи, так и внутри. Для изготовления объемных моделей используются специальные выкройки, вырезаемые из достаточно плотной, хорошо держащей форму, бумаги. Делают и особенные многогранники из бумаги. Схемы таких изделий предусматривают наличие дополнительных, выступающих модулей. Разберем способы, как сконструировать очень красивую фигуру на примере додекаэдра (фото 3).

Как сделать из бумаги многогранник с двенадцатью вершинами: первый способ

Такую фигуру еще называют звездчатым додекаэдром. Каждая из его вершин в своем основании является правильным пятиугольником. Поэтому делают двумя способами такие многогранники из бумаги. Схемы для изготовления будут несколько отличаться друг от друга. В первом случае это единая деталь (фото 4), в результате сворачивания которой получается готовое изделие. Кроме основных граней, на чертеже присутствуют соединительные части для склеивания, благодаря которым фигура смыкается в единое целое. Для изготовления многогранника вторым способом нужно сделать отдельно несколько шаблонов. Рассмотрим процесс работы подробнее.

Как сделать многогранник из бумаги: второй способ

Изготовьте два главных шаблона (фото 5):

— Первый. Нарисуйте на листе окружность и поделите ее поперек на две части. Одна будет основой для выкройки, дугу второй сразу сотрите для удобства. Поделите деталь на пять равных частей и ограничьте все радиусы поперечными отрезками. В результате получатся соединенные вместе пять одинаковых равнобедренных треугольников. Изобразите рядом примыкающую к среднему отрезку точно такую же полуокружность, только в зеркальном отражении. Полученная деталь при сворачивании выглядит как два конуса. Изготовьте таких аналогичных шаблонов всего шесть штук. Для их склеивания используется вторая деталь, которая будет помещаться вовнутрь.

— Второй. Этот шаблон – пятиконечная звезда. Выполните одинаковые двенадцать заготовок. Формируя многогранник, каждую из звезд с подогнутыми вверх концами помещают внутрь конусообразных деталей и приклеивают к граням.

Полный сбор фигуры получается путем соединения двойных блоков дополнительными отрезками бумаги, заводя их вовнутрь. Моделируя изделия, довольно проблематично сделать их разными по размеру. Готовые модели многогранников из бумаги не так-то просто увеличить. Для этого недостаточно просто сделать припуски по всем внешним границам. Нужно масштабировать отдельно каждую из граней. Только так возможно получить увеличенную копию первоначальной модели. Используя второй способ изготовления многогранника, сделать это намного проще, так как будет достаточно увеличить первоначальные заготовки, по которым уже выполняется нужное количество отдельных деталей.

ᐉ Как сделать из бумаги додекаэдр поэтапно. Как сделать икосаэдр из бумаги ✅ igrad.su

Додекаэдром называется правильный многогранник, составленный из двенадцати правильных пятиугольников. Эта эффектная объемная фигура обладает центром симметрии, называемым центром додекаэдра. Кроме того, в ней присутствуют пятнадцать плоскостей симметрии (в каждой грани любая из них проходит через середину противоположного ребра и вершину) и пятнадцать осей симметрии (пересекающих середины параллельных противолежащих ребер). Каждая из вершин додекаэдра является вершиной трех пятиугольников правильной формы.

Свое название конструкция получила по количеству входящих в нее граней (традиционно древние греки давали многогранникам имена, отображающие число граней, составляющих структуру фигуры). Таким образом, понятие «додекаэдр» образовано из значений двух слов: «додека» (двенадцать) и «хедра» (грань). Фигура относится к одному из пяти Платоновых тел (наряду с тетраэдром, октаэдром, гексаэдром (кубом) и икосаэдром). Интересно, что согласно многочисленным историческим документам, все они активно использовались жителями Древней Греции в виде настольных игральных костей и изготавливались из самого различного материала.

Правильные многогранники всегда привлекали людей своей красотой, органичностью и необыкновенным совершенством форм, но додекаэдр имеет особую историю, которая из года в год обрастает все новыми, иногда совершенно мистическими, фактами. Представители многих цивилизаций усматривали в нем сверхъестественную и таинственную сущность, утверждая, что: «Из числа двенадцать произрастает многое». На территориях древних разрушенных государств до сих пор находят маленькие фигурки в виде додекаэдров, выполненные из бронзы, камня или кости. Кроме того, при раскопках на землях современной Англии, Франции, Германии, Венгрии, Италии археологи обнаружили несколько сотен так называемых «римских додекаэдров», датирующихся II-III-м веками нашей эры. Основные размеры фигурок составляют от четырех до одиннадцати сантиметров, причем отличаются они самыми невероятными узорами, текстурами и техникой исполнения. Выдвинутая еще во времена Платона версия о том, что Вселенная представляет собой огромного размера додекаэдр, нашла подтверждение уже в начале XXI -го века. После тщательного анализа данных, полученных при помощи WMAP(многофункционального космического аппарата NASA), ученые согласились с предположением древнегреческих астрономов, математиков и физиков, в свое время занимавшихся вопросами изучения небесной сферы и ее строением. Более того, современные исследователи считают, что наша Вселенная представляет собой бесконечно повторяющийся набор додекаэдров.

Как сделать правильный додекаэдр своими руками

Сегодня конструкция данной фигуры нашла свое отображение во многих вариантах художественного творчества, архитектуре и строительстве. Народные умельцы изготавливают из цветной или белой бумаги необыкновенные по красоте оригами в виде ажурных додекаэдров, а из картона делают оригинальные и прочее). В продаже можно приобрести уже готовые наборы, содержащие все необходимое для изготовления сувениров, но наиболее интересно произвести весь процесс работы своими руками, начиная от построения отдельных деталей и заканчивая сборкой готовой конструкции.

Для того, чтобы сделать правильный додекаэдр из картона, необходим собственно сам материал и подручные средства:

Хорошо иметь тупой нож или какое-либо приспособление для загибания припусков, но если их нет, то вполне подойдет металлическая линейка или те же ножницы.

Делаем правильный додекаэдр

1. Самый первый этап в изготовлении – построение пятиугольника нужного размера. Должен получиться вот такой элемент. Он и станет основой фигуры.
Далее конструируете развертку додекаэдра с учетом припусков на склеивание. В результате получится «выкройка» приблизительно такого вида. Варианты могут различаться, если припуски будут другой формы или размещены на других гранях.
Аккуратно по линиям сгибаете припуски.
Склеиваете.
Наносите на готовый додекаэдр нужный рисунок или декорируете другим выбранным способом.

Как сделать звездчатый додекаэдр

Звездчатые додекаэдры имеют более сложную конструкцию по сравнению с обычными. Эти многогранники подразделяются на малый (первого продолжения), средний (второго продолжения) и большой (последняя звездчатая форма правильного додекаэдра). Каждый из них отличается своими особенностями построения и сборкой. Для работы Вам потребуются те же материалы и инструменты, что и для изготовления стандартного додекаэдра. Если Вы решили сделать первый вариант (малый додекаэдр), то необходимо построить чертеж первого элемента, который станет основой для всей конструкции (в дальнейшем производится ее склеивание или сборка деталей при помощи скрепок).

Делаем звездчатый додекаэдр

Строите схему основной детали нужных размеров с необходимыми припусками. Должен получиться приблизительно такой элемент.
По обозначенным линиям сгибаете, в том числе не забываете о припусках.
Склеиваете каждую деталь по отдельности.
Собираете додекаэдр полностью.
Раскрашиваете или наносите любое из выбранных изображений.

Видео как сделать Додекаэдр:

Представляем Вам некоторые видео как сделать додекаэдр:

И парочку тяжелых, для трудолюбивых..

Оригами додекаэдр

Одной из простейших бумажных кусудам считается додекаэдр-оригами. Но это не значит, что он выглядит неэффектно, особенно когда речь идёт о звёздчатой разновидности. Декоративный многогранник, подобно другим своим родственникам – кусудамам, отлично подходит для праздничного украшения помещений или в качестве оригинального подарка. Мини-додекаэдры можно использовать как модные украшения, сделав из них серьги или кулон.

Ажурная модель

Существует несколько типов оригами-додекаэдров, но сделать эту прозрачную конструкцию из бумажных модулей проще всего. Хорошее задание для детей, желающих познакомиться с азами пространственной геометрии и взрослых, ищущих эффективное средство для снятия стресса. Желательно использовать для игрушки бумагу ками с рисунком, она придаст особый шарм и колорит.

Пошаговая инструкция:

Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
Складываем фигуру по диагонали, как показано на рис 4.
Модули для додекаэдра-кусудамы готовы.

Остаётся соединить их в пространственную композицию. Для этого короткую часть одного модуля вставляем к «карман» длинной части другого. И располагаем так, чтобы внутренние углы и грани обоих элементов совпали.

Аналогичный образом добавляем третий модуль, соединяя его с предыдущими двумя и формируя устойчивый конструктивный узел.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

За счёт необычной бумаги с принтом, получается стильный предмет декора. Чтобы кусудама не распадалась, лучше соединить узловые элементы с помощью клея.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:

Кусудама из правильных пятиугольников

Схема сборки додекаэдра-оригами из пентагонов – равносторонних пятиугольников, разработана американским дизайнером Дэвидом Брилом. Для модулей он использует 12 листов формата А6, то есть 10,5х14,8 см.

Пошаговая инструкция:

Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
Аналогично складываем противоположные углы.
Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
Продолжаем сборку, пока не используем все 12 модулей.

Из подобных додекаэдров часто делают настольные календари. На каждой грани как раз размещается по месяцу. Соответствующие распечатки с числами и днями недели, можно скачать из интернета и наклеить на стенки модели. Получится не только красиво, но и практично.

Додекаэдр-звезда

Правильные звёздчатые многогранники относятся к самым красивым геометрическим фигурам. С момента своего открытия в XVI веке, они считались символом совершенства Вселенной. Малый звёздчатый додекаэдр впервые построил немецкий астроном и математик Иоганн Кеплер – создатель знаменитой теории о строении Солнечной системы. Многогранник имеет собственное имя: Арур Кэли, в честь английского учёного, сделавшего огромный вклад в развитие линейной алгебры.

Малый звёздчатый додекаэдр-оригами представляет собой фигуру из 12 граней-пентаграмм, с пятью пентаграммами, сходящимися к вершинам. Он состоит из 30 модулей, которые складываются из квадратов, размером 8х8 см. Лучше всего использовать профессиональную бумагу-оригами, которая позволит создавать чёткие грани и жёсткие узлы, не позволяющие конструкции распадаться или деформироваться.

Интересные факты о додекаэдре

Правильные многогранники с древних времен восхищали человечество и служили прообразом мирового устройства. Как оказалось, подобные представления небезосновательны. В 2003 году, анализируя данные исследовательского аппарата WMAP, запущенного NASA для изучения фоновых космических излучений, учёные выдвинули гипотезу о додекаэдрическом строении Вселенной по принципу сферы Пуанкаре.

Нечто подобное предполагал и живший в V в. до н. э. древнегреческий философ Платон. В своём учении о классических стихиях, он назвал додекаэдр «образцом божественного устройства Космоса». Вообще же все пять известных правильных многогранников до сих пор называют Платоновыми телами, по имени мыслителя, впервые выстроившего с их помощью чёткую картину мироздания.

Пентагон, лежащий в основе додекаэдра, построен на принципах «золотого сечения». Эта пропорция, которую древние греки считали «божественной» часто встречается в природе. Интересно, что соотношения «золотого сечения» присущи лишь додекаэдру и икосаэдру, у трёх других Платоновых тел его нет.

Игрушки древних римлян

На территориях Европы, некогда принадлежавших Римской империи, до сих пор находят загадочные бронзовые фигурки в форме додекаэдра. Предметы пустотелые, с круглыми отверстиями на каждой стороне и шариками, обозначающими вершины. Учёные пока не смогли однозначно определить функцию этих объектов. Первоначально считалось, что это своеобразные игрушки, однако позднее их отнесли к предметам культа, символизирующим устройство Вселенной. Или Земли, согласно теории, последовательно выдвигаемой с XIX века мировыми физиками, в том числе и российскими.

Впервые о том, что наша планета представляет собой кристалл додекаэдрической формы, заговорили французский математик Пуанкаре и геолог-исследователь де Бемон. Они утверждали, что земная кора, словно футбольный мяч, состоит из 12 правильных пятиугольников, в местах соединения которых, располагаются аномальные зоны и планетарные силовые поля.

В 1920-х годах идею французских коллег подхватил русский физик Степан Кислицын. Он пошёл ещё дальше, заявив, что планета не остаётся в стабильном состоянии, она растёт, из додекаэдра постепенно трансформируясь в икосаэдр. Учёный разработал модели подобных изменений, обозначив узлы гигантской кристаллической сетки, где, по его мнению, располагались месторождения полезных ископаемых: угля, нефти, газа и так далее. В 1928 году Кислицын, опираясь на свои исследования, указал на поверхности земного шара 12 алмазоносных центров, из которых 7 к настоящему времени находятся в активной разработке.

Идеи кристаллического строения планеты продолжают развиваться в XXI веке. Согласно последней гипотезе, подобная структура свойственна всем живым организмам, не только космическим телам, но и человеку. Тем интереснее будет собирать додекаэдр-оригами, чувствуя свою сопричастность к великим тайнам Вселенной.

Оригами: как сделать додекаэдр из бумаги

Додекаэдр — это многогранник, состоящий из 12 одинаковых пятиугольников. Это базовая фигура для множества поделок: от настольных календарей до ажурных подвесных фонариков.

Можно построить пятиугольник самостоятельно — это несложно и гарантирует высокую точность рисунка. Для построения правильного пятиугольника понадобится циркуль и линейка. Нарисуйте круг необходимого размера. Проведите в любом месте радиус. К нему перпендикулярно проведите другой радиус. Затем один из радиусов разделите на две равные части. Каждая половинка будет радиусом другой, маленькой окружности, которая выполнит роль вспомогательной. Затем соедините центр этой вспомогательной окружности с тем местом, где основную окружность пересекает другой радиус (допустим, в точке А). Полученная линия пересечет вспомогательную окружность в определенной точке — В. Расстояние АВ и есть одна десятая часть окружности. Именно это расстояние циркулем отметьте на основной окружности, а затем соедините прямыми линиями эти точки через одну — правильный пятиугольник готов!

Есть и другие методы. Например, пятиугольник можно построить с помощью транспортира, но точности он не гарантирует. Наиболее легий способ — взять готовую схему, распечатать ее и по этой «выкройке» уже мастерить из подходящей бумаги поделку. Но этот способ, несмотря на простоту, подходит не всегда — ведь иногда нужно сделать додекаэдр какого-то конкретного размера. Можно увеличить один пятиугольник до нужного масштаба и распечатать только его, затем построить фигуру по схеме ниже.

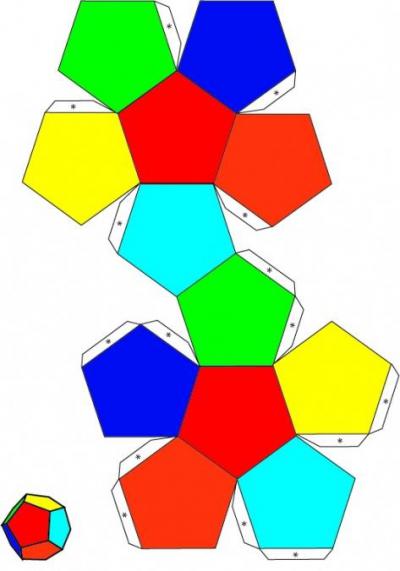
Но «выкройка» — это еще не готовая поделка. Как сделать додекаэдр из бумаги? Для этого понадобятся:

1. Бумага, подходящая по плотности. Она не должна быть слишком тонкой или же слишком толстой — желательно 220 г/м², именно такой плотностью обладает картон, который продают в детских наборах. Хотя из толстого картона вполне можно создавать объемные фигуры, нужно только предварительно обработать все сгибы — слегка надрезать или хорошо продавить, чтобы они хорошо и ровно сгибались.

2. Ножницы, карандаш, клей, вязальная спица или канцелярский нож

Советы по изготовлению додекаэдра

Бумагу в местах сгибов желательно слегка продавить спицей, тупой стороной канцелярского ножа или чем-то острым, но не режущим. Аккуратные ровные сгибы — половина успеха.

Если клея под рукой нет, додекаэдр можно собрать, как конструктор, сделав надрезы по сгибам, а затем просто вставив стороны одна в другую.

Если вы собираете додекаэдр в модульной технике (инструкция ниже), то места соединений желательно проклеивать или закреплять скрепками, поскольку конструкция станет устойчивой только после закрепления последнего модуля.

Додекаэдр в технике оригами

Модуль оригами — отличная основа для додекаэдра. Как сделать додекаэдр из бумаги в модульной технике? Понадобится 30 прямоугольных или квадратных листов бумаги. Каждый из листочков складывается пополам, затем каждую половинку нужно отогнуть в противоположную сторону — получится «гармошка» в четыре сложения. Иногда, если лист не квадратный, делают «гармошку» в три сложения. В итоге у вас в руках узкая промоугольная полоска. Затем с каждой стороны прямоугольника по узкой стороне нужно отогнуть уголок. Уголки складываются в одну сторону — это будущие крепления, которые будут заправляться в «гармошку». Затем согните модуль вовнутрь наискосок по диагонали от маленьких боковых уголков. Таким образом, один модуль для оригами додекаэдра — трехмерный, он включает два ребра будущей фигуры и уголки. Когда все модули готовы, можно начинать сборку.

Сборка начинается с одного узла, для которого необходимо взять три модуля. На рисунке ниже это голубой, розовый и желтый модули оригами. Схемы сборки достаточно просты, и с такими фигурами легко справляются даже начинающие.

Какие поделки можно сделать на основе додекаэдра?

Каждая сторона додекаэдра из бумаги — это плоский пятиугольник, который сам по себе может являться основой для самых разных и причудливых форм. Например, на фото ниже пятиугольник заменен пятиконечнй звездой. Ребра в такой фигуре отсутствуют, хотя предполагаются. Как сделать додекаэдр из бумаги в виде звезды? Замените в развертке, представленной выше, каждый пятиугольник необходимой пятиконечной фигурой и соедините их не по ребрам, а по вершинам.

На этом фото представлен звездчатый додекаэдр. В основе каждого «луча» лежит все тот же пятиугольник.

Вместо пятиугольных пирамид может быть выполнена любая объемная фигура.

На фото ниже в качестве пятиугольников выступают более сложные модули оригами, схемы которых заинтересовавшиеся этой техникой смогут найти в специальной литературе.

В любом случае освоение даже простейшей схемы сборки додекаэдра уже даст огромные возможности для творчества и поиска своих собственных вариантов.

Источники:

http://razuznai.ru/dodekaedr.html
http://all-origami.ru/origami-dodekaedr/
http://fb.ru/article/75832/origami-kak-sdelat-dodekaedr-iz-bumagi

Додекаэдр из бумаги: пошаговая инструкция сборки оригами

Ажурная модель

Пошаговая инструкция:

Для создания кусудамы понадобится 30 одинаковых модулей. Их складывают из прямоугольников, имеющих соотношение сторон 3:4. Например, размером 6х8 см, 9х12 см и так далее. Можно брать как одно-, так и двухсторонние листы.
Складываем каждый прямоугольник пополам вдоль длинной стороны. После чего делаем Z-образный сгиб.
Располагаем получившуюся полоску длинной стороной к себе. Загибаем правый нижний угол вверх. Переворачиваем заготовку на 180°. И повторяем действие для правого нижнего угла (другого).
Складываем фигуру по диагонали, как показано на рис 4.
Модули для додекаэдра-кусудамы готовы.

Продолжаем крепить детали друг к другу, пока не получится объёмная фигура.

Подробная сборка ажурного додекаэдра представлена и в видео-МК:

Кусудама из правильных пятиугольников

Пошаговая инструкция:

Исходный прямоугольник складываем пополам в продольном и поперечном направлении, намечая серединные оси.
Правый верхний и левый нижний угол сгибаем к центру. Получаем своего рода полуконверт.
Аналогично складываем противоположные углы.
Пятиугольную заготовку, «закрываем» сверху вниз «долиной».
Верхний угол опускаем вниз и возвращаем обратно. На месте пересечения получившейся линии с вертикальной осью фигуры, образуется точка. К ней поочерёдно сгибаем внешние углы.
Модуль-пентагон готов. Последние два сгиба раскрываем – это будут детали крепления элементов между собой.
Боковые «ушки» одной детали вставляем в «карманы» другой. Места соединения для надёжности фиксируем клеем.
Продолжаем сборку, пока не используем все 12 модулей.

Додекаэдр-звезда

Интересные факты о додекаэдре

Игрушки древних римлян

Правильные пирамиды — объёмные геометрические тела

Готовый набор «Волшебные грани»

Для сборки многогранников мы можем вам предложить уже готовые развёртки — вырезанные и подогнутые.

Для этого вам нужно воспользоваться деталями набора Волшебные грани № 14.

Кроме того, в самом выпуске вы найдете информацию о строении многогранников.

Сборка правильной четырехугольной пирамиды:

Вращение готового многогранника, собранного из этих деталей:

Сборка усечённой четырехугольной пирамиды:

Вращение готового многогранника, собранного из этих деталей:

Сборка пирамиды со звёздчатым основанием:

Вращение готового многогранника, собранного из этих деталей:

Сборка би-пирамиды с основанием в форме пятиконечной звезды:

Вращение готового многогранника, собранного из этих деталей:

Как собирать многогранники без клея?

Некоторые наши читатели уже высказывали желание отказаться от применения клея.
Да, действительно, от использования клея можно отказаться не меняя конструкции.
Одно из решений – использовать двухсторонний скотч (липкую ленту) предложил видеоблогер Альховик Дмитрий. И непросто предложил, а наглядно продемонстрировал, склеив две модели многогранников из набора «Волшебные грани № 27».

Сборка модели многогранника — Усечённый додекаэдр:

Сборка модели многогранника — Усечённый икосо-додекаэдр в форме тороида:

Сборка модели многогранника — Девятая звёздчатая форма икосаэдра:

Что можно сказать?
Выглядит здорово!

Есть ли возражения против применения двухстороннего скотча «повсеместно»?
Да. Есть.

Дело в том, что у Дмитрия очень высокий уровень мастерства в сборке. Можно сказать – «золотые руки». Каждая операция склеивания выполняется предельно точно. Никаких ошибок и погрешностей. Поэтому для него двухсторонний скотч действительно справедливая замена клея.

Однако для большинства наших читателей, мы рекомендуем продолжить использование клея Супер-ПВА.
Почему? Причина, в том, что липкая лента не простит вам ошибок в отличии от клея. Если вы недостаточно точно приклеили лепесток детали клеем у вас остается некоторое время сдвинуть (подравнять) деталь пока клей не «схватится». Липкая лента такой возможности не даст, с ней надо работать точно и наверняка. Если вы не попали, а лента уже приклеилась, то деталь придется отдирать с силой, что может деформировать всю конструкцию.

Можно, конечно, возразить, на сколько долго такая конструкция на основе липкой ленты сохранит устойчивость и не развалится, так как соединение может быть не настолько крепкое как клеевое? Но и клей бывает разный!

Поэтому последнее слово, использовать или нет клей, мы оставляем за вами!

Звёздчатый октаэдр или соединение двух тетраэдров

— . —

Красная пирамида прознает белую, или наоборот. А может это комплекс пирамид, направленных в разные стороны света. Эти фигуры всегда загадка.

— . —

Представленное изображение данного многогранника иллюстрирует именно второе его название — соединение двух тетраэдров. Так Вы можете представить себе тетраэдр красного цвета, направленный вверх сквозь который проходит бежевый тетраэдр направленный вниз.

Однако математики предпочитают именовать многогранник звёздчатым октаэдром.

Звёздчатый октаэдр можно было бы признать правильным многогранником, так как все его грани — правильные треугольники одинакового размера и все углы между ними равны. Но на самом деле это геометрическое тело не является шестым правильным многогранником наравне с пятью известными Платоновыми телами. Причина в том, что в определении правильного многогранника присутствует слово выпуклый, то есть все грани должны лежать по одну сторону от плоскости, проходящей через любую из них.

История открытия

Звёздчатый октаэдр был впервые изображен в 1509 г. в книге De divina proportione («О божественных пропорциях»). Автором которой являлся математик Лука Пачоли (1445-1514 гг.). А иллюстрация для книги принадлежит руке Леонардо да Винчи.

Звёздчатый октаэдр был выполнен в виде восьми каркасных тетраэдров соединенных между собой.

Затем, спустя почти 100 лет многогранник был переоткрыт Иоганном Кеплером, и назван им Stella octangula — звезда восьмиугольная.

Именно такая иллюстрация звёздчатого октаэдра вызывает споры о том, каким образом был открыт этот многогранник.

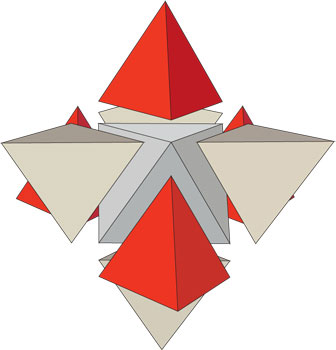
1-й возможный вариант это к сторонам октаэдра присоединить 8 тетраэдров

Или продолжить плоскости параллельные сторонам октаэдра, получив на пересечении плоскостей те же самые 8 тетраэдров. Иными словами, создать звездчатую форму октаэдра.

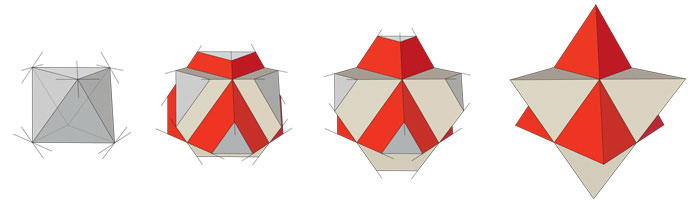
Второй путь: Объединить между собой два тетраэдра.

Что наглядно иллюстрирует окраска граней в два цвета – красный и бежевый.

Видео. Вращение многогранника

Видео. Ролик преобразования

Видео от наших партнеров – команда ART KOSEKOMA, наглядно демонстрирует, как можно преобразовать октаэдр в звездчатую форму и получить два тетраэдра.

Сначала грани октаэдра, вытягиваясь, образуют звёздчатую форму. Затем видео-ролик показывает, как звёздчатый октаэдр можно разложить на два тетраэдра.

Свойства многогранника

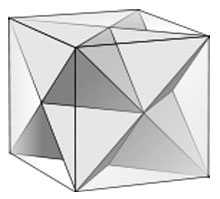
2. Интересная особенность многогранника. Если соединить между собой все остроконечные вершины, то линии пересечения точно соответствуют ребрам куба.

Таким образом, звёздчатый октаэдр может быть вписан в куб.

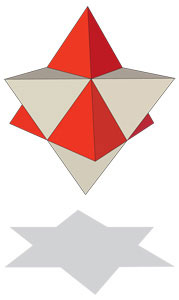
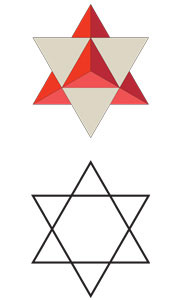
3. Если посмотреть на многогранник сверху, либо на отбрасываемую тень, то контуры рисунка будут создавать правильную шестиугольную звезду.

Шестиугольная звезда в виде двух перекрещивающихся треугольников это древнейший символ, который именуется как Звезда Давида (еще одно название — Печать царя Соломона).

Развертка 1

Первый из предлагаемых вариантов сборки – это склеить звёздчатый октаэдр из единой развертки. Такой вариант наиболее часто можно встретить в учебной литературе. Однако, ограничением является размер листа. В том случае если это лист формата А4, то размеры готового многогранника весьма скромные.

Развертка 2

Второй вариант, когда отдельно собираются октаэдр и 8 заготовок в виде пирамид. Затем к сторонам октаэдра поочередно приклеиваются все заготовки. Данный вариант более предпочтителен для начинающих моделистов.

Развертка 3

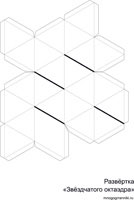
На страницах интернета нам встретился весьма необычный вариант сборки, так же в виде единой развертки.

Готовый набор

Для сборки многогранника мы можем вам предложить уже готовые развёртки — вырезанные и подогнутые.

Для этого вам нужно воспользоваться деталями набора Волшебные грани № 15.

Кроме того, в самом выпуске вы найдете информацию о строении многогранника.

Вращение готового многогранника, собранного из этих деталей:

Подробная сборка от Андрея Ломакина (youtube-канал Sekretmastera)

Подробная сборка от Алексея Жигулева (youtube-канал Оригами)

Складывание бумаги и многогранник — Скачать PDF бесплатно

Словарь форм от YR до Y6

Словарь форм с YR по Y6. Указания. Термины в этом словаре взяты из буклета «Mathematical Vocabulary», выпущенного Национальной стратегией счисления.Детям нужно понимать и использовать

Дополнительная информация

G3-33 Строительные пирамиды

G3-33 Строительство пирамид Цель: Учащиеся будут строить каркасы пирамид и описывать свойства пирамид. Требуемые предварительные знания: многоугольники: треугольники, четырехугольники, пятиугольники, шестиугольники Словарь:

Дополнительная информация

Набор заданий 4. Руководство для тренера

Геометрия и измерение твердых фигур. Набор упражнений 4. Руководство для инструктора Mid_SGe_04_TG Авторские права принадлежат McGraw-Hill Companies. McGraw-Hill Professional Development ГЕОМЕТРИЯ И ИЗМЕРЕНИЕ ТВЕРДЫХ ФИГУР

Дополнительная информация

E XPLORING ЧЕТЫРЕХСТОРОННИЙ

E XPLORING QUADRILATERALS E 1 Состояние геометрии Цель 9: использовать геометрические методы для анализа, категоризации и заключения о точках, линиях, плоскостях и пространстве.Заявление о целях: Действия в этом

Дополнительная информация

Твердые тела, сетки и поперечные сечения

Твердые тела, сетки и поперечные сечения Многогранники В этом разделе мы рассмотрим различные трехмерные фигуры, известные как твердые тела. Начнем с обсуждения многогранников. Многогранник Многогранник — трехмерный

Дополнительная информация

Геометрия минералов

Геометрия минералов Цели Учащиеся соединят геометрию и естественные науки. Учащиеся будут изучать двух- и трехмерные формы. Учащиеся узнают числовые отношения и запишут алгебраические выражения

Дополнительная информация

Обучение и изучение трехмерной геометрии

Эта публикация предназначена для поддержки и воодушевления учащихся начальной подготовки учителей.Он предоставит им математический предмет и педагогические знания, необходимые для преподавания трехмерной геометрии

Дополнительная информация

Отрезки, лучи и линии

ГЛАВНАЯ ССЫЛКА Сегменты линии, лучи и семейство линий Примечание Помогите ребенку сопоставить каждое имя, указанное ниже, с правильным рисунком линии, луча или сегмента линии. Затем понаблюдайте, как ваш ребенок рисует линейкой

Дополнительная информация

ОТКРЫТИЕ 3D-ФОРМ

,ОТКРЫТИЕ РАБОЧИХ ЛИСТОВ 3D-ФОРМ ОКТЯБРЬ-ДЕКАБРЬ 2009 1. Рабочий лист 1. Вырежьте и приклейте фигуры. ФОРМЫ, КОТОРЫЕ ФОРМИРУЕТ ВАЛКУ СЛАВИ 2. Рабочий лист 2: ЗАПОЛНИТЕ КАРТЫ Сфера, треугольник, призма,

Дополнительная информация

Дорогие семьи 4-х классов,

Дорогие семьи 4-х классов! В течение следующих нескольких недель наш класс будет изучать геометрию. Посредством повседневной деятельности мы будем изучать взаимосвязь между плоскими двухмерными фигурами и твердыми трехмерными фигурами

Дополнительная информация

Глоссарий по алгебре и геометрии.Угол 90

lgebra Геометрия Глоссарий 1) острый угол угол меньше 90 острый угол 90 угол 2) острый треугольник треугольник, все углы которого меньше 90 3) смежные углы углы, которые имеют общий отрезок Пример:

Дополнительная информация

Задача месяца: разрезание куба

Задача месяца: Задачи месяца (POM) используются по-разному, чтобы способствовать решению проблем и способствовать внедрению первого стандарта математической практики из Common Core State Standards:

Дополнительная информация

Оригами, Папирофальтен, Папирофлексия: складывание бумаги в математическом образовании Р.Алан Рассел, доктор философии, доцент математики, Университет Илона,

Оригами, Папирофальтен, Папирофлексия: складывание бумаги в математическом образовании Р. Алан Рассел, доктор философии, доцент математики, Университет Илона, Илон, Северная Каролина, США [email protected] Abstract

Дополнительная информация

Геометрия и измерения

Студент сможет: Геометрия и измерение 1.Продемонстрировать понимание принципов геометрии, измерения и операций с использованием измерений. Использовать американскую систему измерения для

Дополнительная информация

Урок 4: Площадь поверхности

Урок 4: Площадь поверхности. Выбранные стандарты содержимого. Адресация тестов: M-1-M. Применение понятий длины, площади, площади поверхности, объема, емкости, веса, массы, денег, времени, температуры и скорости для

Дополнительная информация

Примечания по геометрии ПЕРИМЕТР И ПЛОЩАДЬ

Периметр и площадь Страница 1 из 57 ПЕРИМЕТР И ПЛОЩАДЬ Цели: После завершения этого раздела вы должны уметь делать следующее: Рассчитывать площадь заданных геометрических фигур.Рассчитываем периметр

Дополнительная информация

Объем пирамид и конусов

Объем пирамид и конусов. Цель: предоставить опыт исследования взаимосвязей между объемами геометрических тел. www.everydaymathonline.com презентации etoolkit Algorithms

Дополнительная информация

Урок 4: Площадь поверхности

Урок 4: Оценка эталона стандартов содержания выбранной площади поверхности M.3 Оценка, вычисление и применение физических измерений с использованием подходящих единиц (например, расчет периметра и площади плоских фигур,

Дополнительная информация

12 Площадь и объем поверхности

12 Площадь поверхности и объем 12.1 Трехмерные фигуры 12.2 Площадь поверхности призм и цилиндров 12.3 Площадь поверхности пирамид и конусов 12.4 Объемы призм и цилиндров 12.5 Объемы пирамид

Дополнительная информация

Светящаяся в темноте геометрия

Большая идея Светящаяся в темноте геометрия На этой неделе вы будете делать геометрические фигуры из светящихся палочек.Дети попробуют все размеры и формы треугольников и четырехугольников, а затем раскладывают палочки в мистическом

Дополнительная информация

Успех по математике 6 класс

T276 Успех по математике, 6 класс [ЗАДАЧА] Ученик будет складывать и вычитать с десятичными знаками до тысячных в математических и реальных ситуациях. [ПРЕДВАРИТЕЛЬНЫЕ НАВЫКИ] сложение и вычитание

Дополнительная информация

РУКОВОДСТВО ДЛЯ УЧИТЕЛЯ ПО ЧАСУ РАБОТЫ

Использование головоломок для обучения решению проблем РУКОВОДСТВО ДЛЯ УЧИТЕЛЯ «Час пик» включает «Час пик 2, 3, 4», «Час пик младший»., Railroad Rush Hour и Safari Rush Hour ПРЕИМУЩЕСТВА Час пик — это раздвижная головоломка, которая

Дополнительная информация

РАСПИСАНИЕ: МАТЕМАТИКА 2007

, K РАСПИСАНИЕ РАБОТЫ: МАТЕМАТИКА 00 СРОК МОДУЛЯ … LO ЧИСЛА, ОПЕРАЦИИ И ОТНОШЕНИЯ Способен распознавать, представлять числа и их отношения, а также подсчитывать, оценивать, вычислять и проверять

Дополнительная информация

Рисование трехмерных объектов в перспективе

Учебные материалы по математике SAS #.1 (по одному на пару студентов) SAS # .2 (по одному на пару студентов) TIS # .1 (прозрачность) TIS # .2 (прозрачность) TIS # .3 (подсказка журнала) Изометрическая точечная бумага Изометрическая

Дополнительная информация

Тесселяция с помощью правильных многоугольников

Тесселяция с помощью правильных многоугольников Вы, наверное, видели пол, выложенный квадратной плиткой. Квадраты — хорошая плитка, потому что они могут покрывать поверхность без зазоров или перекрытий.Этот вид плитки

Дополнительная информация

ME 111: Инженерный чертеж

ME 111: Лекция по инженерному черчению № 14 (10.10.2011) Разработка поверхностей http://www.iitg.ernet.in/arindam.dey/me111.htm http://www.iitg.ernet.in/rkbc /me111.htm http://shilloi.iitg.ernet.in/~psr/ Индийский

Дополнительная информация

Дроби в 1 степени

Дроби в 1 классе. Понимание дробей и беглость владения дробями были серьезной проблемой и препятствием для концептуальных знаний наших учащихся о дробях и взаимосвязях между ними.Эта установка

Дополнительная информация

Однодюймовая миллиметровая бумага

Однодюймовая миллиметровая бумага для работы в классе Blackline Master II — 1 49 Полудюймовая миллиметровая бумага для работы в классе 50 стратегий в классе Blackline Master II — 2 Двухсантиметровая миллиметровая бумага для работы в классе Blackline Master

Дополнительная информация

1 Симметрии правильных многогранников

1230, примечания 5 1 Симметрии правильных многогранников Группы симметрии Напомним: Групповые аксиомы: Предположим, что (G, ·) — группа, а a, b, c — элементы G.Тогда (i) a b G (ii) (a b) c = a (b c) (iii) существует

Дополнительная информация

МАТЕМАТИЧЕСКАЯ СТУДЕНЧЕСКАЯ КНИГА. 8 класс, блок 6

КНИЖКА ДЛЯ УЧАЩИХСЯ ПО МАТЕМАТИКЕ 8 класс Блок 6 Блок 6 Измерение Математика 806 Введение в измерения 3 1. Угловые измерения и окружности 5 Классификация и измерение углов 5 Перпендикулярные и параллельные линии, часть 1 12 Перпендикуляр

Дополнительная информация

Сью Файн Линн Маскелл

ВЕСЕЛЫЕ + ИГРЫ = МАТЕМАТИКА Сью Файн Линн Маскелл Учителя часто обеспокоены тем, что на уроках математики не хватает времени на игры.Но на самом деле есть время поиграть в игры, и нам нужно убедиться, что

Дополнительная информация

Дублирование сегментов и углов

КОНКРЕТНЫЙ УРОК 3.1 Дублирование сегментов и элементов На этом уроке вы узнаете, что означает создание геометрической конструкции. Дублируйте сегмент с помощью линейки, циркуля и пирожка

Дополнительная информация

Формула многогранника Эйлера | plus.maths.org

Июнь 2007 г.

Леонард Эйлер, 1707 — 1783

Давайте начнем с представления главного героя этой истории — формулы Эйлера:

В — E + F = 2.

Несмотря на простоту, эта маленькая формула заключает в себе фундаментальное свойство тех трехмерных тел, которые мы называем многогранниками , которые очаровывали математиков более 4000 лет. На самом деле я могу пойти дальше и сказать, что формула Эйлера говорит нам нечто очень глубокое о форме и пространстве.Формула носит имя известного швейцарского математика Леонарда Эйлера (1707–1783), которому в этом году исполнилось бы 300 лет.

Что такое многогранник?

Прежде чем мы рассмотрим, что говорит нам формула Эйлера, давайте рассмотрим многогранники более подробно. Многогранник — это твердый объект, поверхность которого состоит из множества плоских граней , которые сами по себе ограничены прямыми линиями. Каждая грань на самом деле представляет собой многоугольник , замкнутую форму на плоской 2-мерной плоскости, состоящую из точек, соединенных прямыми линиями.

Рис. 1. Знакомые треугольник и квадрат являются многоугольниками, но многоугольники также могут иметь более неправильную форму, как показано справа.

В многоугольниках не допускается наличие отверстий, как показано на рисунке ниже: левая фигура здесь является многоугольником, а правая — нет.

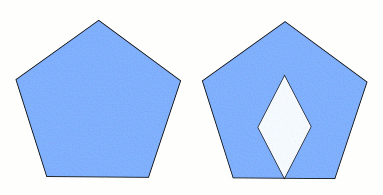
Рис. 2. Фигура слева — многоугольник, а фигура справа — нет, потому что в ней есть «дыра».

Многоугольник называется правильным , если все его стороны имеют одинаковую длину и все углы между ними одинаковы; треугольник и квадрат на рисунке 1 и пятиугольник на рисунке 2 правильные.

Многогранник — это то, что вы получаете, когда перемещаетесь на одно измерение вверх. Это замкнутый твердый объект, поверхность которого состоит из множества многоугольных граней. Мы называем стороны этих граней ребрами — две грани встречаются вдоль каждой из этих граней. Назовем углы граней вершинами , так что любая вершина лежит как минимум на трех разных гранях. Чтобы проиллюстрировать это, вот два примера
всем известные многогранники.

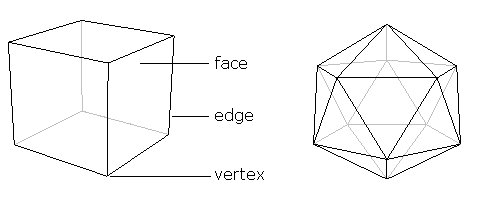
Рис. 3. Знакомый куб слева и икосаэдр справа.Многогранник состоит из многоугольных граней , их стороны известны как ребер , а углы — как вершин .

Многогранник состоит только из одной части. Он не может, например, состоять из двух (или более) в основном отдельных частей, соединенных только ребром или вершиной. Это означает, что ни один из следующих объектов не является истинным многогранником.

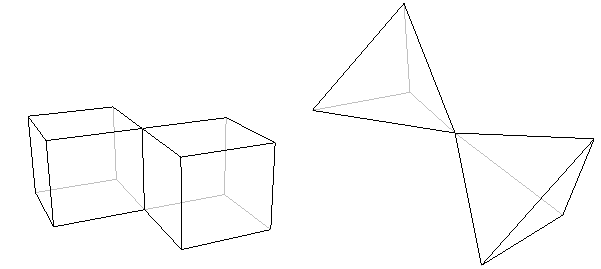
Рисунок 4: Эти объекты не являются многогранниками, потому что они состоят из двух отдельных частей, которые встречаются только на ребре (слева) или вершине (справа).

Что нам говорит формула?

Теперь мы готовы посмотреть, что формула Эйлера говорит нам о многогранниках. Посмотрите на многогранник, например куб или икосаэдр выше, посчитайте количество вершин, которые у него есть, и назовите это число V . Куб, например, имеет 8 вершин, поэтому V = 8 . Затем посчитайте количество ребер многогранника и назовите это число E . У куба 12 ребер, поэтому в случае
куб E = 12 .Наконец, посчитайте количество лиц и назовите его F . В случае с кубом F = 6 . Теперь формула Эйлера говорит нам, что

В — E + F = 2;

или, говоря словами: количество вершин минус количество ребер плюс количество граней равно двум.

В случае с кубом мы уже видели, что V = 8, E = 12 и F = 6 . Итак,

В — E + F = 8 — 12 + 6 = 14 — 12 = 2

, что говорит нам формула Эйлера.Если мы теперь посмотрим на икосаэдр, мы обнаружим, что V = 12, E = 30 и F = 20 . Сейчас,

В — E + F = 12-30 + 20 = 32-30 = 2,
как мы и ожидали.

Формула Эйлера верна для куба и икосаэдра. Оказывается, довольно красиво, что это верно для почти для каждого многогранника . Единственные многогранники, для которых это не работает, — это те, в которых есть отверстия, как показано на рисунке ниже.

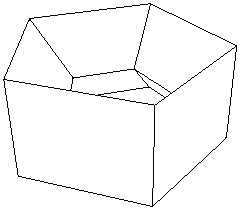
Рис. 5: В этом многограннике сквозное отверстие.Формула Эйлера в этом случае не выполняется.

Эти многогранники называются непростыми , в отличие от многогранников без отверстий, которые называются простыми . Непростые многогранники, возможно, не первое, что приходит в голову, но их много, и мы не можем избежать того факта, что формула Эйлера не работает ни с одним из них. Однако даже этот неловкий факт стал частью совершенно новой теории космоса.
и форма.

Сила формулы Эйлера

Всякий раз, когда математики сталкиваются с инвариантным признаком, свойством, истинным для целого класса объектов, они знают, что натолкнулись на что-то хорошее.Они используют его, чтобы исследовать, какими свойствами может обладать отдельный объект, и определить свойства, которые должны иметь все они. Формула Эйлера может сказать нам, например, что не существует простого многогранника с
ровно семь граней. Вам не нужно садиться с картоном, ножницами и клеем, чтобы узнать это — формула — это все, что вам нужно. Аргумент, показывающий, что не существует семигранного многогранника, довольно прост, так что взгляните на него, если вам интересно.

Используя аналогичным образом формулу Эйлера, мы можем обнаружить, что не существует простого многогранника с десятью гранями и семнадцатью вершинами.Призма, показанная ниже, в основе которой лежит восьмиугольник, действительно имеет десять граней, но число вершин здесь шестнадцать. Пирамида, имеющая 9-гранное основание, также имеет десять граней, но имеет десять вершин. Но формула Эйлера говорит нам, что ни один простой многогранник не имеет
ровно десять граней и семнадцать вершин.

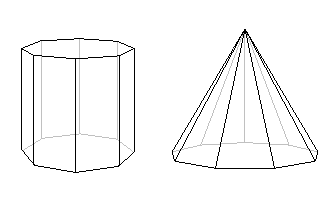
Рисунок 6: Оба этих многогранника имеют десять граней, но ни у одного из них нет семнадцати вершин.

Именно такие соображения приводят нас к, вероятно, самому прекрасному открытию из всех.Он включает Платоновых тел , хорошо известный класс многогранников, названный в честь древнегреческого философа Платона, в трудах которого они впервые появились.

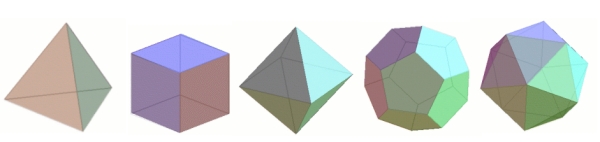
Рисунок 7: Платоновы тела. Слева направо мы видим тетраэдр с четырьмя гранями, куб с шестью гранями, октаэдр с восемью гранями, додекаэдр с двенадцатью гранями и икосаэдр с двадцатью гранями.

Хотя их симметричная элегантность сразу бросается в глаза, когда вы смотрите на приведенные выше примеры, на самом деле не так-то просто описать это словами.Оказывается, это описывается двумя особенностями. Во-первых, у Платоновых тел нет выступов или провалов, поэтому они имеют красивую округлую форму. Другими словами, это означает, что всякий раз, когда вы выбираете две точки в Платоновом теле и рисуете
прямая линия между ними, этот кусок прямой линии будет полностью заключен в твердое тело — Платоново твердое тело — это то, что называется выпуклым . Вторая особенность, называемая регулярностью , заключается в том, что все грани твердого тела представляют собой правильные многоугольники с одинаковым количеством сторон и одинаковое количество ребер выходит из каждой вершины твердого тела.

Куб правильный, так как все его грани — квадраты и из каждой вершины выходит ровно три ребра. Вы можете сами убедиться, что тетраэдр, октаэдр, икосаэдр и додекаэдр тоже правильные.

Теперь вы можете задаться вопросом, сколько существует различных Платоновых Тел. С момента открытия куба и тетраэдра математиков настолько привлекла элегантность и симметрия Платоновых тел, что они искали больше и пытались перечислить их все.Здесь на помощь приходит формула Эйлера. Вы можете использовать ее, чтобы найти все возможности для количества граней, ребер и
вершины правильного многогранника. Вы обнаружите, что на самом деле существует только пять различных правильных выпуклых многогранников! Это очень удивительно; в конце концов, количество различных правильных многоугольников не ограничено, так почему мы должны ожидать здесь ограничения? Пять Платоновых Тел — это тетраэдр, куб, октаэдр, икосаэдр и додекаэдр, показанные выше.

Доказательство

Рене Декарт,
(1596–1650)

Игра с различными простыми многогранниками покажет вам, что формула Эйлера всегда верна. Но если вы математик, этого недостаточно. Вам понадобится доказательство, водостойкий логический аргумент, который показывает, что это действительно работает для всех многогранников , включая те, которые у вас никогда не будет времени проверить.

Адриан-Мари Лежандр, (1752 — 1833)

Несмотря на название формулы, на самом деле не Эйлер предложил первое полное доказательство.Его история сложна, насчитывает 200 лет и включает в себя некоторых из величайших математиков, в том числе Рене Декарта (1596–1650), самого Эйлера, Адриана-Мари Лежандра (1752–1833) и Августена-Луи Коши (1789–1857).

Огюстен-Луи Коши, (1789 — 1857)

Интересно отметить, что все эти математики использовали очень разные подходы для доказательства формулы, каждый из которых поражал своей изобретательностью и проницательностью. Однако это доказательство Коши, и я хотел бы дать вам здесь представление.Его метод состоит из нескольких этапов и шагов. Первый этап включает построение так называемой сети .

Формирование сети

Представьте, что вы держите свой многогранник одной стороной вверх. Теперь представьте, что вы «удаляете» только эту грань, оставляя края и вершины вокруг нее позади, так что у вас есть открытая «коробка». Затем представьте, что вы можете держаться за коробку и отодвинуть края отсутствующей грани друг от друга. Если вы потянете их достаточно далеко, коробка расплющится и превратится в сеть точек и линий.
в плоской плоскости.Приведенная ниже серия диаграмм иллюстрирует этот процесс применительно к кубу.

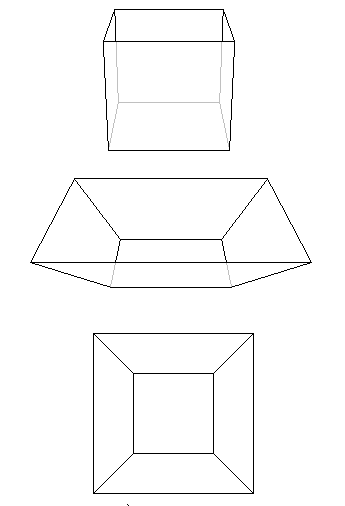
Рисунок 8: Превращение куба в сеть.

Как вы можете видеть из диаграммы выше, каждая грань многогранника становится областью сети, окруженной ребрами, и это то, что мы будем называть гранью сети. Это внутренние грани сети. Также существует внешняя грань , состоящая из области вне сети; это соответствует той грани, которую мы удалили из многогранника.Итак, у сети есть вершины,
прямые края и многоугольные грани.

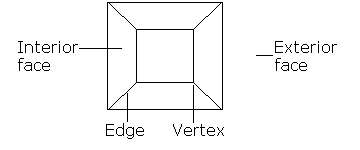
Рисунок 9: Сеть имеет грани, ребра и вершины.

При формировании сети вы не добавляли и не удаляли вершины, поэтому сеть имеет то же количество вершин, что и многогранник — V . Сеть также имеет такое же количество ребер — E — что и многогранник. Теперь о лицах; все грани многогранника, кроме «недостающей», оказываются «внутри» сети.Отсутствующее лицо стало внешним лицом, которое тянется
по всей сети. Итак, включая внешнюю грань, в сети насчитывается F граней. Таким образом, вы можете использовать сеть , а не сам многогранник, чтобы найти значение V — E + F . Теперь мы продолжим преобразование нашей сети, чтобы упростить вычисление этого значения.

Преобразование сети

Есть три типа операций, которые мы можем выполнять в нашей сети.Мы представим три этапа, связанных с ними.

Step 1 Мы начинаем с рассмотрения полигональных граней сети и спрашиваем: существует ли грань с более чем тремя сторонами? Если есть, мы рисуем диагональ, как показано на схеме ниже, разделяя лицо на две меньшие грани.

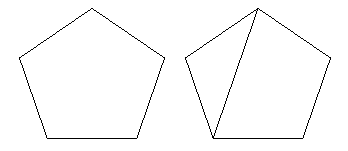
Рис. 10: Разделение граней.

Мы повторяем это с выбранным лицом, пока лицо не будет разбито на треугольники.

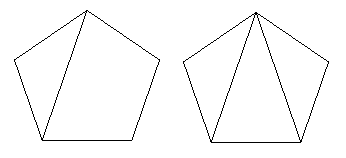
Рис. 11: В итоге у нас остались треугольные грани.

Если есть еще одна грань с более чем тремя сторонами, мы используем Шаг 1 для этой грани, пока она тоже не будет разбита на треугольные грани. Таким образом, мы можем разбить каждую грань на треугольные грани и получить новую сеть, все грани которой треугольные. Мы проиллюстрируем этот процесс, показав, как преобразовать сеть, которую мы создали из куба.

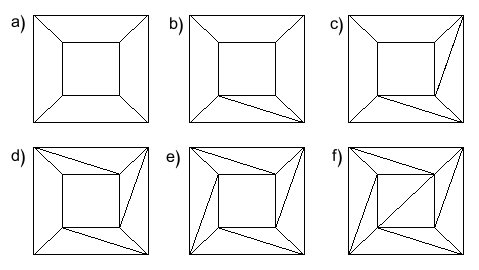
Рисунок 12: Вот что происходит с сетью куба, когда мы неоднократно выполняем Шаг 1.

Мы возвращаемся к шагу 1 и смотрим на сеть, которую мы получаем после выполнения шага 1 только один раз.Теперь, нарисовав диагональ, мы добавили одно ребро. Наше исходное лицо стало двумя лицами, поэтому мы добавили одно к количеству лиц. Мы не изменили количество вершин. Теперь сеть имеет V, вершин, E + 1 ребер и F + 1 граней. Так как же
V — E + F изменилось после того, как мы выполнили шаг 1 один раз? Используя то, что мы знаем об изменениях в V , E и F , мы можем видеть, что V — E + F превратилось в V — (E + 1) + (F + 1) .Теперь у нас

В — (E + 1) + (F + 1) = V — E — 1 + F + 1 = V — E + F.

Итак, V — E + F имеет , не изменилось после шага 1! Поскольку каждое использование шага 1 оставляет V — E + F неизменным, оно остается неизменным, когда мы достигаем нашей новой сети, состоящей полностью из треугольников! Влияние на V — E + F при преобразовании сети, созданной из куба, показано в таблице ниже.

Круглый	В	E	Ф	В — E + F
(а)	8	12	6	2
б)	8	13	7	2
(в)	8	14	8	2
(г)	8	15	9	2
д)	8	16	10	2
(ж)	8	17	11	2

Теперь мы представляем шаги 2 и 3.Они будут удалять грани снаружи сети, шаг за шагом уменьшая количество граней. Как только мы начнем это делать, сеть, вероятно, больше не будет представлять собой многогранник, но важное свойство сети сохранится.

Step 2 Проверяем, есть ли в сети грань, которая имеет только одно ребро с внешней гранью. Если это так, мы удаляем эту грань, удаляя одно общее ребро. Область, которая была покрыта выбранной нами гранью, становится частью внешней грани, и сеть имеет новую границу.Это проиллюстрировано схемой ниже для сети, построенной из куба.

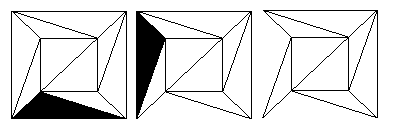
Рис. 13: Удаление граней с одной внешней кромкой.

Теперь возьмем V , E и F в качестве количества вершин, ребер и граней, которые сеть, состоящая из треугольных граней, имела до выполнения шага 2. Теперь посмотрим, как число V — E + F изменился после выполнения шага 2 один раз. Мы удалили одно ребро, поэтому наша новая сеть имеет E — 1 ребер.Мы не трогали вершины в
все, так что у нас остается V вершин. Грань, которую мы использовали для шага 2, была объединена с внешней гранью, так что теперь у нас есть F — 1 граней. Итак, V — E + F превратилось в V — (E — 1) + (F — 1) и

.
В — (E — 1) + (F — 1) = V — E + 1 + F — 1 = V — E + F.

Итак, еще раз V — E + F не изменился.

Step 3 Проверяем, есть ли у нашей сети грань, которая имеет два общих ребра с внешней гранью.Если это так, мы удаляем эту грань, удаляя оба этих общих ребра и их общую вершину, так что снова область, принадлежащая нашей выбранной грани, становится частью внешней грани. Это проиллюстрировано ниже на примере сети, созданной из куба, после выполнения шага 2.
дважды.

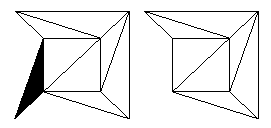
Рис. 14: Удаление граней с двумя внешними кромками.

Как и раньше, теперь возьмем V , E и F как количество вершин, ребер и граней сети, с которой мы начинаем.Теперь, как шаг 3 повлиял на число V — E + F ? Мы удалили одну вершину — ту, которая находится между двумя ребрами, — теперь осталось V — 1 вершин. Мы удалили два ребра, так что теперь есть
E — 2 кромок. Наконец, наша выбранная грань слилась с внешней гранью, так что теперь у нас есть F — 1 граней. Итак, V — E + F превратилось в (V — 1) — (E — 2) — (F — 1) и

.
(V — 1) — (E -2) + (F — 1) = V — 1 — E + 2 + F — 1 = V — E + F.

Итак, еще раз V — E + F не изменился.

Секрет доказательства заключается в выполнении последовательности шагов 2 и 3 для получения очень простой сети. Напомним, что мы неоднократно использовали шаг 1 для создания сети только с треугольными гранями. Эта сеть обязательно будет иметь грань, которая имеет ровно одно ребро с внешней гранью, поэтому мы берем эту грань и выполняем Шаг 2. Мы можем выполнить Шаг 2 на нескольких гранях, по одной, пока не появится
появляется грань, имеющая два ребра с внешней гранью.Затем мы можем выполнить шаг 3, используя это лицо. Мы продолжаем выполнять шаги 2 и 3 и продолжаем удалять лица таким образом.

При этом необходимо соблюдать два важных правила. Во-первых, мы всегда должны выполнять Шаг 3, когда это возможно; если есть выбор между Шагом 2 и Шагом 3, мы всегда должны выбирать Шаг 3. В противном случае сеть может распасться на отдельные части. Во-вторых, мы должны удалять лица только по одному. Если мы этого не сделаем, мы можем закончить тем, что края сами по себе будут торчать наружу.
лицо, и у нас больше не будет нормальной сети.Чтобы проиллюстрировать процесс, мы выполним несколько шагов в сети куба, продолжая с того места, где мы оставили его на последней диаграмме.

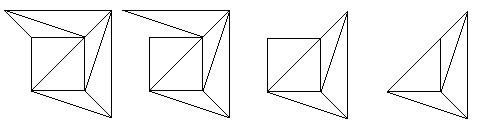
Рисунок 15: Применение нашего алгоритма к сети куба.

Теперь мы можем задать себе один или два вопроса. Останавливается ли когда-нибудь этот процесс удаления лиц, и если да, то с чем мы остались? Небольшое размышление покажет вам, что он должен остановиться — мы можем удалить только конечное число граней и ребер — и когда это произойдет, у нас останется один треугольник.Вы можете увидеть несколько диаграмм, описывающих весь процесс для сети, сформированной из додекаэдра (напомним, что это было одно из Платоновых тел, представленных ранее).

Теперь посмотрите на количество вершин, ребер и граней, присутствующих в нашей последней сети — единственном треугольнике. У нас V = 3 , E = 3 и F = 2 — мы все равно должны включить внешнюю грань. Сейчас

В — E + F = 3 — 3 + 2 = 2.

На протяжении всего процесса, начиная с полного многогранника и заканчивая треугольником, значение V — E + F не менялось.Итак, если V — E + F = 2 для конечной сети, мы также должны иметь V — E + F = 2 для самого многогранника! Доказательство закончено!

За многогранниками

В заключение я упомяну некоторые следствия формулы Эйлера за пределами мира многогранников. Я начну с очень маленького: компьютерных чипов. Компьютерные микросхемы — это интегральные схемы, состоящие из миллионов мелких компонентов, связанных миллионами проводящих дорожек. Они напоминают наши сети выше, , за исключением , которые обычно невозможно разложить в плоскости.
без некоторых проводящих дорожек — краев — пересечения.Крестовины — плохая вещь в схемотехнике, поэтому их следует ограничивать, но найти подходящее расположение — непростая задача. Формула многогранника Эйлера с ее информацией о сетях является важным ингредиентом в поиске решений.

Теперь перейдем к очень большому: нашей Вселенной. По сей день космологи не пришли к единому мнению о его точной форме. Основным для их рассмотрения является топология , математическое исследование формы и пространства. В XIX веке математики обнаружили, что все поверхности в трехмерном пространстве по существу характеризуются количеством отверстий, которые у них есть: наши простые многогранники не имеют отверстий,
пончик имеет одно отверстие и т. д.Формула Эйлера не работает для многогранников с дырками, но математики обнаружили захватывающее обобщение. Для любого многогранника V — E + F ровно в 2 минус 2 раза больше количества отверстий! Оказывается, это число, называемое эйлеровой характеристикой , имеет решающее значение для изучения всех трехмерных поверхностей, а не только многогранников.
Формулу Эйлера можно рассматривать как катализатор совершенно нового мышления о форме и пространстве.

Об авторе

Аби выросла на севере Англии и переехала на юг, чтобы изучать математику в Имперском колледже в Лондоне и Королеве Марии в Лондонском университете.Сейчас она преподает математику в Открытом университете. Главный математический интерес Аби — теория групп. Когда она писала эту статью, ей очень понравилось исследовать тайны формулы Эйлера.

c ++ — Как превратить поверхностную сетку в многогранник?

Переполнение стека

Около
Товары
Для команд

Переполнение стека
Общественные вопросы и ответы
Переполнение стека для команд
Где разработчики и технологи делятся частными знаниями с коллегами
работы
Программирование и связанные с ним технические возможности карьерного роста
Талант
Нанимайте технических специалистов и создавайте свой бренд работодателя
реклама
Обратитесь к разработчикам и технологам со всего мира
О компании